多策略改进海鸥优化算法

目录

一、非线性参数A策略

二、翻筋斗觅食策略 

       基本 SOA 有一些局限性，例如容易陷入局部最优值、后期收敛缓慢、勘探与开发能力不平衡等，在求解复杂优化问题时尤甚。为了改善基本SOA的不足，提出一种基于翻筋斗觅食策略的改进 SOA(SFSOA)。需要强调的是，所提 SFSOA 不改变基本 SOA 的算法框架，仅通过引入两种新策略改善SOA的性能。

一、非线性参数A策略

       在SOA中，海鸥个体的迁移行为是算法的一种重要操作，通过引入一个参数A来控制海鸥个体位置，避免海鸥个体在飞行寻优过程中与其他相邻个体发生碰撞，不产生重复的位置。因此，参数A在SOA搜索过程中对平衡算法的勘探和开采能力起重要作用。然而，参数A的值随迭代次数增加从线性递减到0。一般来说，fc的取值为2,即在SOA迭代过程中A的值由2线性减少至0。

       在利用SOA解决优化问题中，其搜索过程非常复杂且呈现出一个非线性下降趋势。同时，待求问题也需要算法的探索性和开发性行为发生非线性变化，以避免局部最优解。若控制参数A纯粹地以线性递减的方式模拟海鸥群体的迁移过程，就会降低SOA的寻优搜索能力。因此，本文提出一种基于倒S型函数的非线性递减控制参数A策略，其数学表达式为:

       其中： 和分别为频率控制参数的最大值和最小值。从式(12)可知，在SOA的寻优过程中，参数A的值以非线性方式进行递减可增强算法的全局搜索能力，同时既能避开海鸥个体之间的位置重叠，也可在全局探索和局部开发能力上获得一个较好的平衡。图1给出了控制参数A的值随迭代次数增加以非线性递减方式变化的曲线。

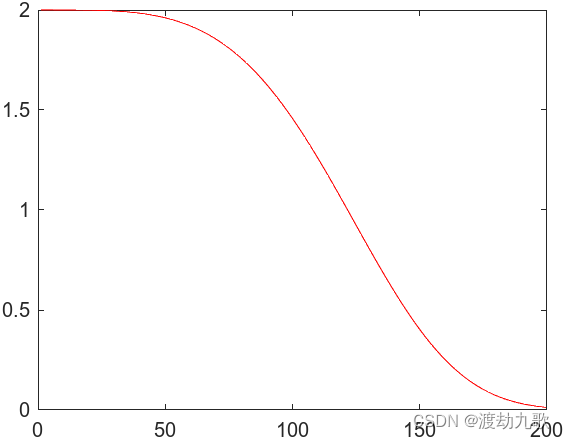
图1 控制参数A的值随迭代次数增加曲线

        从图1可以清晰地看出，与式(3)相比，式(12)有两个不同的特征：a)非线性变化参数A更符合海鸥群体的实际迁移过程，前后期递减缓慢和中期递减加快的特点能提高SOA的精度和加快收敛；b)非线性变化参数A在迭代过程中更趋向于局部开发搜索(约占最大迭代次数的60%)。 

二、翻筋斗觅食策略 

       在算法搜索后期，所有海鸥个体均向当前群体中最优个体所在区域靠拢；导致群体多样性会损失，如果当前最优个体不是全局最优解，则算法陷入局部最优，这是群体智能优化算法的固有的缺点。为了克服这个缺点，研究者在群体智能优化算法中引入许多策略如变异算子、反向学习、莱维飞行、透镜成像学习、小孔成像学习等。翻筋斗觅食是蝠鲼在捕食时最有效的一种方式，当找到食物源时，它们会做一系列向后翻筋斗动作，围绕浮游生物(猎物)旋转，将其吸引到自己身边。原理实现如下：在这种策略中，猎物的位置被视为一个支点，每只蝠鲼都倾向于围绕枢轴和翻筋斗来回游动到一个新的位置，其数学模型为：

其中：为蝠鲼个体位置；是当前全局最优个体位置；称为空翻因子；和分别是[0,1]的随机数。为了降低 SOA 在搜索后期陷入局部最优的概率，将蝠鲼翻筋斗觅食策略引入到 SOA中，其数学表达式为:

 其中，空翻因子，海鸥翻筋斗觅食示意图如图2所示。

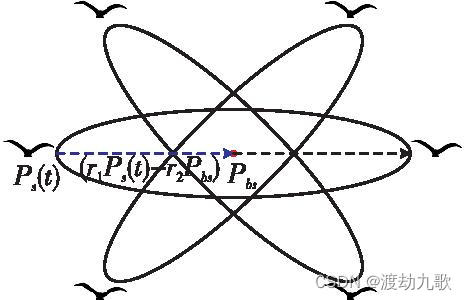
图2 海鸥翻筋斗觅食示意图

        从图2和式(14)可以看出，在定义了翻筋斗范围后，每只海鸥都可以移动到新搜索域中的任何位置，该搜索域位于当前位置与其围绕目前找到的最佳海鸥位置的对称位置之间。随着当前海鸥个体位置与目前找到的最佳海鸥位置之间的距离减小，当前位置的扰动也会减小，所有个体逐渐逼近搜索空间中的最优解。因此，随着迭代次数的增加，翻筋斗觅食的范围自适应地减小，从而加速收敛。组合上述两个策略改进SOA,得到的ISOA流程如图3所示。

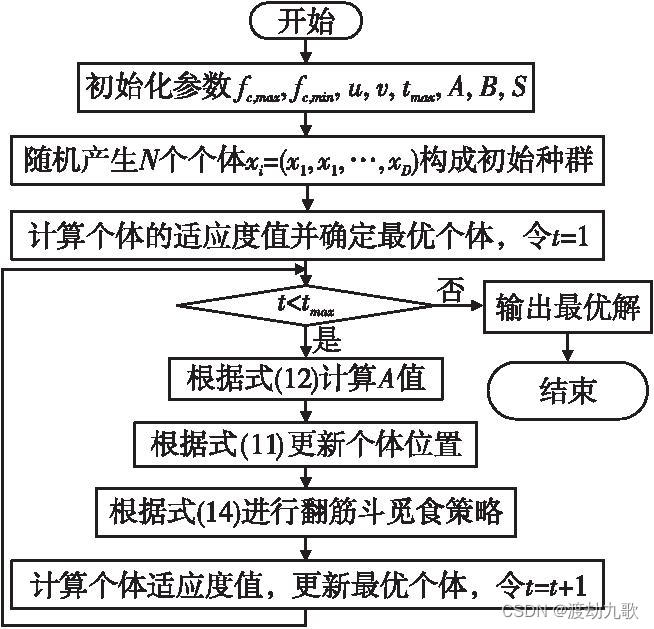
图3 ISOA流程图