本文主要是介绍Python求解数值积分-定积分求解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本小节求解下述定积分:
∫ 0.7 4 ( c o s ( 2 π x ) e − x + 1.2 ) d x \int_{0.7}^4(cos(2πx)e^{-x}+1.2)\mathrm{d}x ∫0.74(cos(2πx)e−x+1.2)dx
版权声明
本文可以在互联网上自由转载,但必须:注明出处(作者:海洋饼干叔叔)并包含指向本页面的链接。
本文不可以以纸质出版为目的进行改编、摘抄。
本文节选自作者的《Python编程基础及应用》视频教程。
数值积分-integrate
integrate模块提供了好几种数值积分的方法,包括常微分方程组(ODE)的数值积分。相关函数列表如下:
| 函数名 | 作用 | 函数名 | 作用 |
|---|---|---|---|
| quad() | 一元定积分 | dblquad() | 二元定积分 |
| triquad() | 三元定积分 | odeint() | 计算常微分方程组的数值解 |
微实践 - 定积分求解
本小节求解下述定积分:
∫ 0.7 4 ( c o s ( 2 π x ) e − x + 1.2 ) d x \int_{0.7}^4(cos(2πx)e^{-x}+1.2)\mathrm{d}x ∫0.74(cos(2πx)e−x+1.2)dx
为了方便说明,我们先使用下述代码画出示意图:
import numpy as np
from matplotlib import pyplot as pltx = np.linspace(0,6,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2plt.axis([np.min(x),np.max(x),0,np.max(y)]) #坐标范围
plt.plot(x,y,label="$cos(2πx)e^{-x}+1.2$") #画曲线,带图示
plt.fill_between(x,y1=y,y2=0,where=(x>=0.7)&(x<=4), #填充积分区域facecolor='blue',alpha=0.2)
plt.text(0.5*(0.7+4),0.4,r"$\int_{0.7}^4(cos(2πx)e^{-x}+1.2)\mathrm{d}x$",horizontalalignment='center',fontsize=14) #增加说明文本
plt.legend() #显示图示
plt.show()
执行结果:
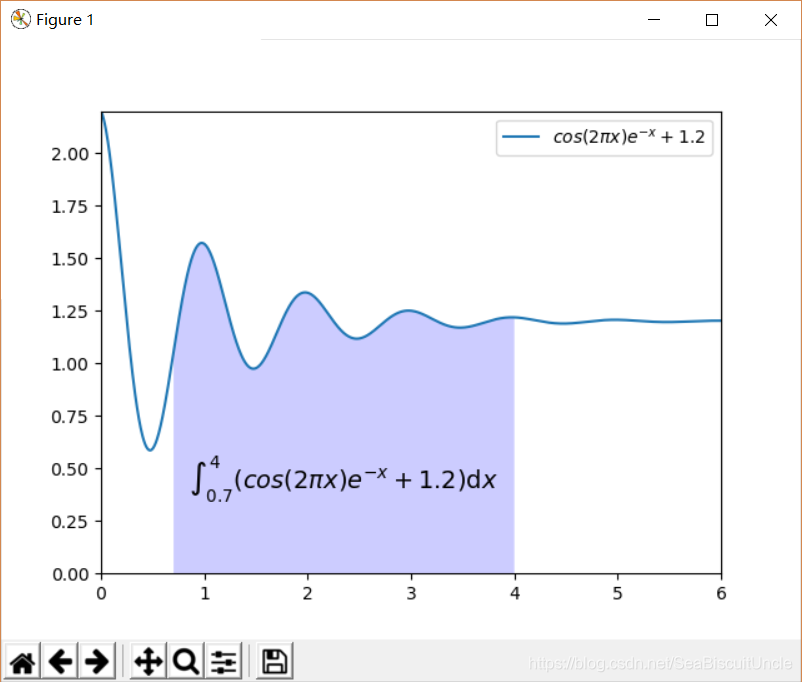
plt.axis()函数设定了图的坐标范围。fill_between(x,y1=y,y2=0,where=(x>=0.7)&(x<=4)…)则用于填充积分区域,其中,x和y1构成曲线1; x和y2=0构成曲线2(也就是横坐标线);该函数填充两条曲线之间x值域为[0.7,4]的部分,where参数指明了这个值域。facecolor指定填充颜色,alpha参数指定透明度。
plt.text()则在图上添加文本,前两个参数指定了文本的坐标位置,horizontalalignment='center’要求文本在指定的位置水平居中摆放(指定位置位于文本的水平中心)。r"$…$"为文本内容:字符串前加表示放弃对字符串内的内容进行\转义;两个"为文本内容:字符串前加r表示放弃对字符串内的内容进行\转义;两个$包含起来说明其中的内容为LaTeX格式的公式。
显然,上述定积分就是上图中阴影部分的面积。
方法1:分成小矩形,计算面积和
import numpy as npx = np.linspace(0.7,4.0,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2
dx = x[1] - x[0] #每个矩形的宽度
fArea = np.sum(y*dx) #矩形宽*高,再求和
print("Integral area:",fArea)
执行结果:
Integral area: 4.032803310221616
上述代码中,把曲线的阴影部分分成1000个矩形,每个矩形的宽都是dx,第i个矩形的高则是yi。每个矩形的长乘宽,再求和,得积分面积。
方法2:使用quad()函数进行积分
import math
from scipy import integratedef func(x):print("x=",x) #用于展示quad()函数对func的多次调用return math.cos(2*math.pi*x)*math.exp(-x)+1.2fArea,err = integrate.quad(func,0.7,4)
print("Integral area:",fArea)
执行结果:
x= 2.35
x= 0.7430542279466668
x= 3.9569457720533334
x= 2.4613227224815875
...
x= 3.4178741117287044
Integral area: 4.029065401143393
首先,我们定义了一个函数func(),它根据x计算y值。当对单个数值进行计算时,numpy的ufunc并不具备速度优势,所以我们使用了math模块。
integrate.quad()专门用于计算一元定积分,fArea,err = integrate.quad(func,0.7,4)取x值域[0.7,4]进行数值积分,在积分过程中,会反复调用func()函数计算y值。其返回一个元组,包括积分结果及误差。
integrate.quad()计算的积分会比方法1的矩形面积求和方法更加精确。
本文节选自作者的《Python编程基础及应用》视频教程及同名教科书。想完整零基础学习Python程序设计,欢迎使用此免费视频教程。

这篇关于Python求解数值积分-定积分求解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






