【算法刷题】—7.16前缀和、哈希表、双指针的结合

• 🧛‍♂️个人主页：杯咖啡
• 💡进步是今天的活动，明天的保证！
• ✨目前正在学习：SSM框架,算法刷题
• 🙌牛客网，刷算法过面试的神级网站，用牛客你也牛。 👉免费注册和我一起学习刷题👈
• 🐳希望大家多多支持🥰一起进步呀！
• 😎Sometimes accompanied,sometimes alone,stay awesome all the time.
  聚散终有时，潇洒走一回。-《纽约，纽约》

✨今日算法三题

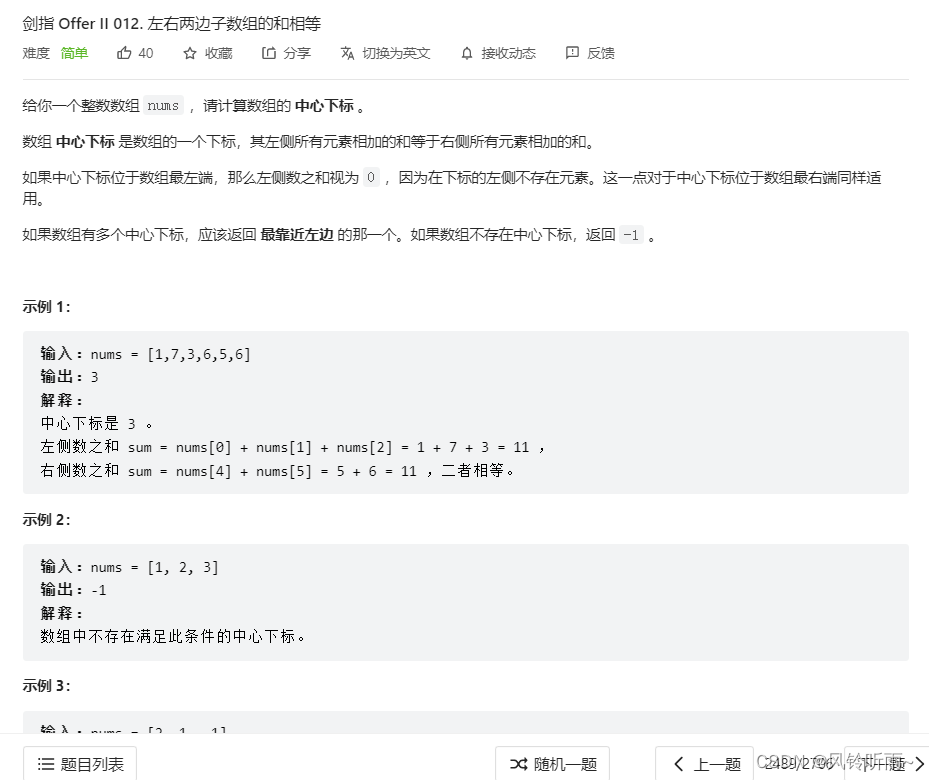
1.左右两边子数组的和相等
2.和可被K整除的子数组
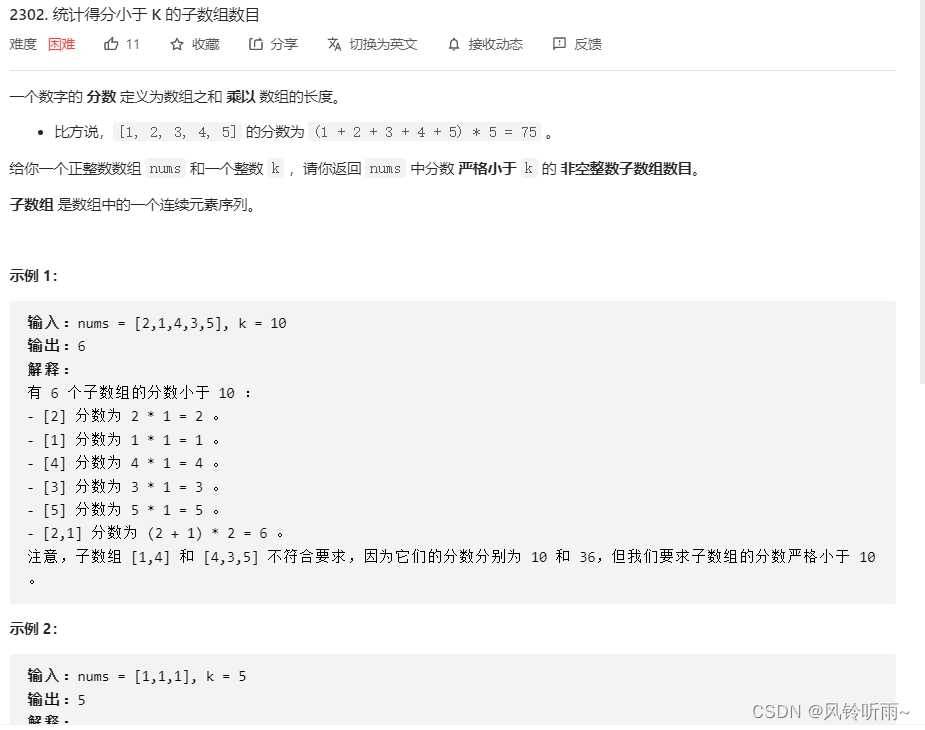
3.统计得分小于K的子数组

1.左右两边子数组的和相等

题目描述

思路详解

本题我们可以采用遍历解决，记数组的全部元素之和为 total，当遍历到第 i 个元素时，设其左侧元素之和为 sum，则其右侧元素之和为total−numsi−sum。左右侧元素相等即为sum=total−numsi−sum，即 2×sum+numsi=total。

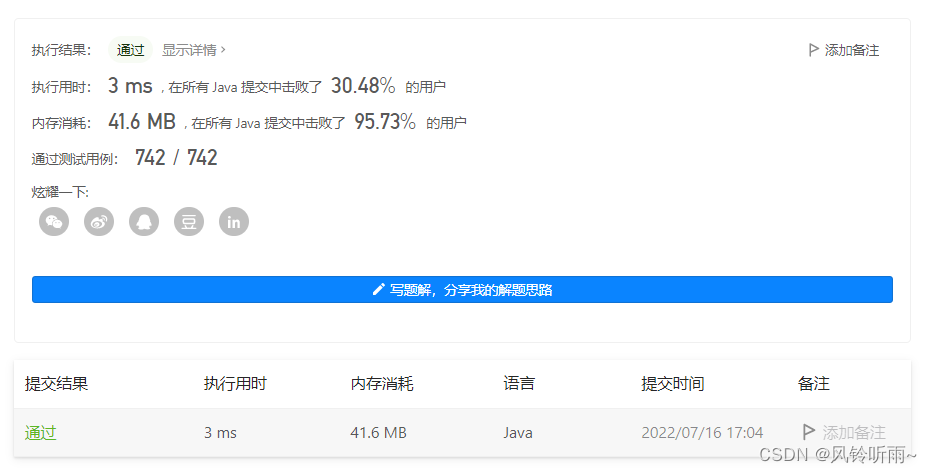
代码与结果

class Solution {public int pivotIndex(int[] nums) {int total = Arrays.stream(nums).sum();int sum = 0;for (int i = 0; i < nums.length; ++i) {if (2 * sum + nums[i] == total) {return i;}sum += nums[i];}return -1;}
}

2.和可被K整除的子数组

题目描述

思路详解

本题我们可以采用前缀和解决，令P[i]=nums[0]+nums[1]+…+nums[i]。那么每个连续子数组的和sum(i,j) 就可以写成 P[j]−P[i−1]（其中0<i<j）的形式。此时，判断子数组的和能否被 k 整除就等价于判断(P[j]−P[i−1]) mod k == 0，根据 同余定理，只要 P[j] mod k==P[i−1] mod k，就可以保证上面的等式成立。

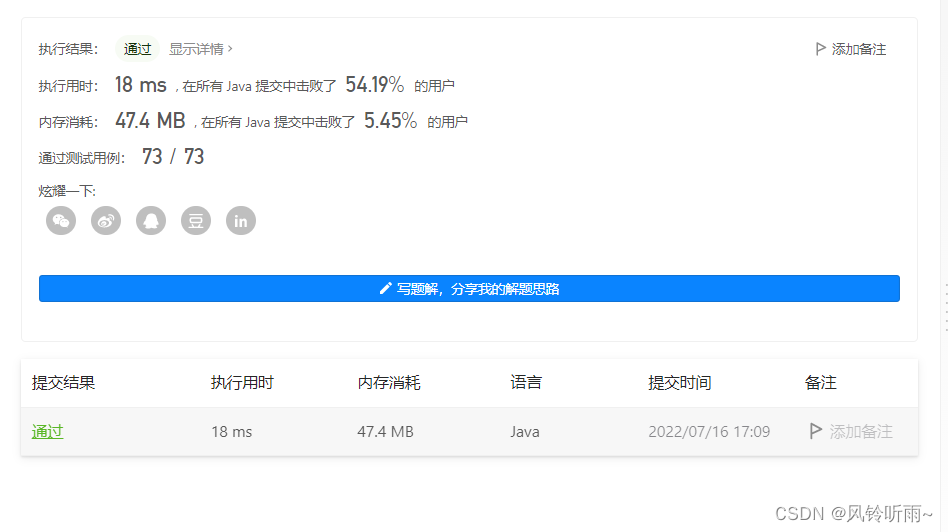
代码与结果

class Solution {public int subarraysDivByK(int[] nums, int k) {Map<Integer, Integer> record = new HashMap<Integer, Integer>();record.put(0, 1);int sum = 0, ans = 0;for (int elem : nums) {sum += elem;// 注意 Java 取模的特殊性，当被除数为负数时取模结果为负数，需要纠正int modulus = (sum % k + k) % k;int same = record.getOrDefault(modulus, 0);ans += same;record.put(modulus, same + 1);}return ans;}
}

3.统计得分小于K的子数组

题目描述

思路详解

本题使用双指针，双指针使用前提：
1.子数组（连续）；
2.有单调性。
本题元素均为正数，这意味着只要某个子数组满足题目要求，在该子数组内的更短的子数组同样也满足题目要求。
做法：枚举子数组右端点，去看对应的合法左端点的个数，那么根据上面的前提 2，我们需要求出合法左端点的最小值。

代码与结果

class Solution {public long countSubarrays(int[] nums, long k) {long ans = 0L, sum = 0L;for (int left = 0, right = 0; right < nums.length; right++) {sum += nums[right];while (sum * (right - left + 1) >= k)sum -= nums[left++];ans += right - left + 1;}return ans;}
}

✨总结

今天主要练习了前缀和的使用，尤其前缀和的考察一般不会单独出题，往往结合其他算法来达到时间复杂度的优化。

$原创不易，还希望各位大佬支持一下$

$点赞，你的认可是我创作的动力！$

$收藏，你的青睐是我努力的方向！$

$评论，你的意见是我进步的财富！$