关于二叉树（创建、遍历、画图）（个人学习使用，非专业）

2023-11-09 00:40
文章标签 二叉树 遍历 学习 使用 创建 个人 画图 非专业

本文主要是介绍关于二叉树（创建、遍历、画图）（个人学习使用，非专业），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目要求

主要内容：

设计一个与二叉树基本操作相关的程序。

程序基本要求如下：

①以树状形式输出；

②以先序、中序、后序三种方式输出；

③统计输出二叉树的结点总数、叶子总数、树高。

目录

题目要求

一、源代码

二、分析

三、基础函数：

1、构造二叉树

2、三个遍历

3、计算结点总数、叶子结点树、树高

基础函数的运行举例

 4、画图部分（有需要的小伙伴可以画图分析就很好理解了）

这里有误解！！！

修改之后 

再次修改：此次修改是为了不让两个元素贴在一起，但是外观还是有瑕疵

一、源代码

#include <bits/stdc++.h>
using namespace std;
#define Max 200typedef struct Node{char date;  //结点数据域struct Node *lchild,*rchild;    //左右孩子指针int x,y;    //横纵坐标
}Node,*tree;char t[Max][Max];//我们规定画布大小为：Max * Max
int minX=Max,maxX=0;//函数声明
void index();
void creatTree(tree &T ,int x,int y);
void paintTree(tree T);
void DLR(tree &T);
void LDR(tree T);
void LRD(tree T);
int countNode(tree T);
int countLeaf(tree T);
int treeHigh(tree T);int main() {index();tree T;while (1){cout << "请选择要执行的操作： ";int choose;cin >> choose;switch (choose) {case 0://创建case 1: {//调试用例：ab#df##g##cx##e##cout << "请按先序输入，以#为结束： ";creatTree(T, 0, 0);break;}//画树case 2 : {int h=treeHigh(T);cout << "画树如下：" <<endl;memset(t,' ',sizeof(t));paintTree(T);for(int i=0;i<2*h;i++){for(int j=minX;j<=maxX;j++){cout << t[j][i];}cout << endl;}break;}//三序遍历case 3:{cout << "先序遍历的结果为： ";DLR(T);cout << endl;cout << "中序遍历的结果为： ";LDR(T);cout << endl;cout << "后序遍历的结果为： ";LRD(T);cout << endl;break;}//树的属性case 4:{cout << "结点总数： "<< countNode(T) << endl;cout << "叶子总数： "<< countLeaf(T) << endl;cout << "树的高度： "<< treeHigh(T) << endl;break;}default :cout << "请选择合法的操作" <<endl;}}
}//菜单
void index()
{cout << "********** 功能如下 **********" << endl;cout << "\t" << "0 ----> 退出程序" << endl;cout << "\t" << "1 ----> 先序建立一个树" << endl;cout << "\t" << "2 ----> 画二叉树" << endl;cout << "\t" << "3 ----> 三序遍历" << endl;cout << "\t" << "4 ----> 树的属性" << endl;
}//画图
void paintTree(tree T)
{if(T){// Max/2的使用目的是：由于原坐标是关于y轴对称的，因此我们要将整个图像沿x轴平移if(' '== t[T->x + Max/2][2 * T->y]) t[T->x + Max/2][2 * T->y]=T->date;//修改之后else t[T->x + Max/2+1][2 * T->y]=T->date;    //若有字符，后移//修改之前：// else t[T->x + Max/2][2 * T->y]='!'; //重复就显示'！'if(T->lchild){t[T->x + Max/2 -1][2 * T->y +1]='/';paintTree(T->lchild);}if(T->rchild){t[T->x + Max/2 +1][2 * T->y +1]='\\';paintTree(T->rchild);}}
}//先序建立二叉树，并且给出坐标
void creatTree(tree &T ,int x,int y)
{char c;cin >> c;if(c == '#') T=NULL;else{   //传值T=new Node;T->date=c;	T->x=x;T->y=y;creatTree(T->lchild,x-2,y+1); //左子树坐标，次数横坐标偏移量为2是为了方便在中间插入'/'creatTree(T->rchild,x+2,y+1); //右子树坐标//更新最小最大横坐标maxX=max(maxX,x+Max/2+1);	minX=min(minX,x+Max/2-1);}
}
//先序遍历
void DLR(tree  &T)
{if(T){cout << T->date << " ";DLR(T->lchild);DLR(T->rchild);}
}
//中序遍历
void LDR(tree T)
{if(T){LDR(T->lchild);cout << T->date << " ";LDR(T->rchild);}
}
//后序遍历
void LRD(tree T)
{if(T){LRD(T->lchild);LRD(T->rchild);cout << T->date << " ";}
}
//结点总数
int countNode(tree T)
{int l,r;//左右子树的结点数if(!T) return  0;if(!T->rchild && T->rchild) return 1;else{l= countNode(T->lchild);r= countNode(T->rchild);return l+r+1;}
}
//叶子总数
int countLeaf(tree T)
{int leaf;if(!T) return  0;if(!T->rchild && !T->rchild) return 1;else leaf= countLeaf(T->lchild)+ countLeaf(T->rchild);return  leaf;
}
//树高
int treeHigh(tree T)
{int lh,rh;if(!T) return 0;else{lh= treeHigh(T->lchild);rh= treeHigh(T->rchild);return lh>rh ? lh+1 : rh+1;}
}

二、分析

由于我们题目要求画图，这里我打算使用坐标，故而我们将结构体定义如下：

typedef struct Node{char date;  //结点数据域struct Node *lchild,*rchild;    //左右孩子指针int x,y;    //横纵坐标
}Node,*tree;

这里我选择用一个二维数组作为画布：

char t[Max][Max];//我们规定画布大小为：Max * Max

三、基础函数：

1、构造二叉树

//先序建立二叉树，并且给出坐标
void creatTree(tree &T ,int x,int y)
{char c;cin >> c;if(c == '#') T=NULL;else{   //传值T=new Node;T->date=c;	T->x=x;T->y=y;creatTree(T->lchild,x-2,y+1); //左子树坐标，次数横坐标偏移量为2是为了方便在中间插入'/'creatTree(T->rchild,x+2,y+1); //右子树坐标}
}

2、三个遍历

//先序遍历
void DLR(tree  &T)
{if(T){cout << T->date << " ";DLR(T->lchild);DLR(T->rchild);}
}
//中序遍历
void LDR(tree T)
{if(T){LDR(T->lchild);cout << T->date << " ";LDR(T->rchild);}
}
//后序遍历
void LRD(tree T)
{if(T){LRD(T->lchild);LRD(T->rchild);cout << T->date << " ";}
}

3、计算结点总数、叶子结点树、树高

//结点总数
int countNode(tree T)
{int l,r;//左右子树的结点数if(!T) return  0;if(!T->rchild && T->rchild) return 1;else{l= countNode(T->lchild);r= countNode(T->rchild);return l+r+1;}
}
//叶子总数
int countLeaf(tree T)
{int leaf;if(!T) return  0;if(!T->rchild && !T->rchild) return 1;else leaf= countLeaf(T->lchild)+ countLeaf(T->rchild);return  leaf;
}
//树高
int treeHigh(tree T)
{int lh,rh;if(!T) return 0;else{lh= treeHigh(T->lchild);rh= treeHigh(T->rchild);return lh>rh ? lh+1 : rh+1;}
}

基础函数的运行举例

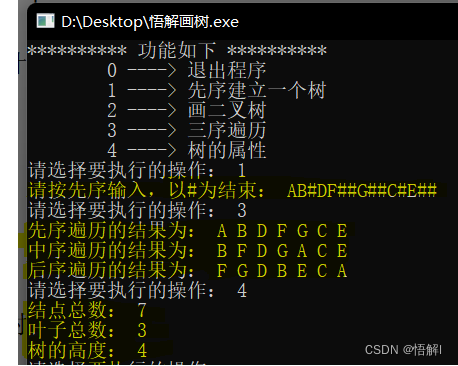
本次用到的输入样例：AB#DF##G##C#E##

图示如下：

 结果如下：（黄色部分）

 

 4、画图部分（有需要的小伙伴可以画图分析就很好理解了）

原版：

//画图1（此函数以美观为主）
void paintTree(tree T)
{if(T){// Max/2的使用目的是：由于原坐标是关于y轴对称的，因此我们要将整个图像沿x轴平移if(' '== t[T->x + Max/2][2 * T->y]) t[T->x + Max/2][2 * T->y]=T->date;else t[T->x + Max/2][2 * T->y]='!'; //重复就显示'！'if(T->lchild){t[T->x + Max/2 -1][2 * T->y +1]='/';paintTree(T->lchild);}if(T->rchild){t[T->x + Max/2 +1][2 * T->y +1]='\\';paintTree(T->rchild);}}
}

结果如下：

 

这里有误解！！！

我们更换一个测试用例：124##5##36##7##

用例结构如下：

 运行结果如下：

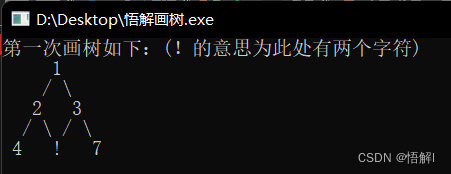
修改之后 

在次我们可以看到，这个办法会隐藏一部分的数据，当然我们也可以加以修改：

//画图1（此函数以美观为主）
void paintTree(tree T)
{if(T){// Max/2的使用目的是：由于原坐标是关于y轴对称的，因此我们要将整个图像沿x轴平移if(' '== t[T->x + Max/2][2 * T->y]) t[T->x + Max/2][2 * T->y]=T->date;//修改之后：else t[T->x + Max/2+1][2 * T->y]=T->date;//修改之前：// else t[T->x + Max/2][2 * T->y]='!'; //重复就显示'！'if(T->lchild){t[T->x + Max/2 -1][2 * T->y +1]='/';paintTree(T->lchild);}if(T->rchild){t[T->x + Max/2 +1][2 * T->y +1]='\\';paintTree(T->rchild);}}
}

运行结果如下：

再次修改：此次修改是为了不让两个元素贴在一起，但是外观还是有瑕疵

测试用例：aaaa##a##aa##a##aaa##a##aa##a##

void paintTreeplus(tree T,int l,int r)
{int mid=(l+r)/2;if(T){t[mid][2 * T->y]=T->date;if(T->lchild){for(int i=(mid+l)/2;i<mid;i++) t[i][2 * T->y+1] ='/';paintTreeplus(T->lchild,l,mid);}if(T->rchild){for(int i=mid+1;i<=(mid+r)/2;i++) t[i][2 * T->y+1] ='\\';paintTreeplus(T->rchild,mid,r);}}
}
int main()
{int minX=0,maxX=pow(2,h)+1;paintTreeplus(T,minX,maxX);for(int i=0;i<2*h;i++){for(int j=minX;j<=maxX;j++){cout << t[j][i];}cout << endl;}
}

运行结果如下：

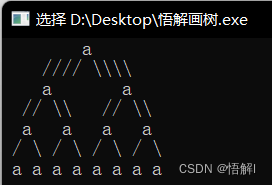
你悟解了吗

本篇为个人学习阶段所写，请各位大佬多多斧正。

这篇关于关于二叉树（创建、遍历、画图）（个人学习使用，非专业）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/373281。

相关文章

Java使用Thumbnailator库实现图片处理与压缩功能

Java使用Thumbnailator库实现图片处理与压缩功能

《Java使用Thumbnailator库实现图片处理与压缩功能》Thumbnailator是高性能Java图像处理库,支持缩放、旋转、水印添加、裁剪及格式转换,提供易用API和性能优化,适合Web应... 目录1. 图片处理库Thumbnailator介绍2. 基本和指定大小图片缩放功能2.1 图片缩放的
阅读更多...
Python使用Tenacity一行代码实现自动重试详解

Python使用Tenacity一行代码实现自动重试详解

《Python使用Tenacity一行代码实现自动重试详解》tenacity是一个专为Python设计的通用重试库,它的核心理念就是用简单、清晰的方式,为任何可能失败的操作添加重试能力,下面我们就来看... 目录一切始于一个简单的 API 调用Tenacity 入门：一行代码实现优雅重试精细控制：让重试按我
阅读更多...
MySQL中EXISTS与IN用法使用与对比分析

MySQL中EXISTS与IN用法使用与对比分析

《MySQL中EXISTS与IN用法使用与对比分析》在MySQL中,EXISTS和IN都用于子查询中根据另一个查询的结果来过滤主查询的记录,本文将基于工作原理、效率和应用场景进行全面对比... 目录一、基本用法详解1. IN 运算符2. EXISTS 运算符二、EXISTS 与 IN 的选择策略三、性能对比
阅读更多...
使用Python构建智能BAT文件生成器的完美解决方案

使用Python构建智能BAT文件生成器的完美解决方案

《使用Python构建智能BAT文件生成器的完美解决方案》这篇文章主要为大家详细介绍了如何使用wxPython构建一个智能的BAT文件生成器,它不仅能够为Python脚本生成启动脚本,还提供了完整的文... 目录引言运行效果图项目背景与需求分析核心需求技术选型核心功能实现1. 数据库设计2. 界面布局设计3
阅读更多...
使用IDEA部署Docker应用指南分享

使用IDEA部署Docker应用指南分享

《使用IDEA部署Docker应用指南分享》本文介绍了使用IDEA部署Docker应用的四步流程：创建Dockerfile、配置IDEADocker连接、设置运行调试环境、构建运行镜像,并强调需准备本... 目录一、创建 dockerfile 配置文件二、配置 IDEA 的 Docker 连接三、配置 Do
阅读更多...
Android Paging 分页加载库使用实践

Android Paging 分页加载库使用实践

《AndroidPaging分页加载库使用实践》AndroidPaging库是Jetpack组件的一部分,它提供了一套完整的解决方案来处理大型数据集的分页加载,本文将深入探讨Paging库... 目录前言一、Paging 库概述二、Paging 3 核心组件1. PagingSource2. Pager3.
阅读更多...
python使用try函数详解

python使用try函数详解

《python使用try函数详解》Pythontry语句用于异常处理,支持捕获特定/多种异常、else/final子句确保资源释放,结合with语句自动清理,可自定义异常及嵌套结构,灵活应对错误场景... 目录try 函数的基本语法捕获特定异常捕获多个异常使用 else 子句使用 finally 子句捕获所
阅读更多...
C++11右值引用与Lambda表达式的使用

C++11右值引用与Lambda表达式的使用

《C++11右值引用与Lambda表达式的使用》C++11引入右值引用,实现移动语义提升性能,支持资源转移与完美转发；同时引入Lambda表达式,简化匿名函数定义,通过捕获列表和参数列表灵活处理变量... 目录C++11新特性右值引用和移动语义左值 / 右值常见的左值和右值移动语义移动构造函数移动复制运算符
阅读更多...
Python对接支付宝支付之使用AliPay实现的详细操作指南

Python对接支付宝支付之使用AliPay实现的详细操作指南

《Python对接支付宝支付之使用AliPay实现的详细操作指南》支付宝没有提供PythonSDK,但是强大的github就有提供python-alipay-sdk,封装里很多复杂操作,使用这个我们就... 目录一、引言二、准备工作2.1 支付宝开放平台入驻与应用创建2.2 密钥生成与配置2.3 安装ali
阅读更多...
C#中lock关键字的使用小结

C#中lock关键字的使用小结

《C#中lock关键字的使用小结》在C#中,lock关键字用于确保当一个线程位于给定实例的代码块中时,其他线程无法访问同一实例的该代码块,下面就来介绍一下lock关键字的使用... 目录使用方式工作原理注意事项示例代码为什么不能lock值类型在C#中，lock关键字用于确保当一个线程位于给定实例的代码块中时
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2