本文主要是介绍如何保证数据的安全?对称和非对称加密,身份认证,摘要算法,数字证书等傻傻分不清?波哥图解带你彻底掌握,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
支付安全
1.基础概念
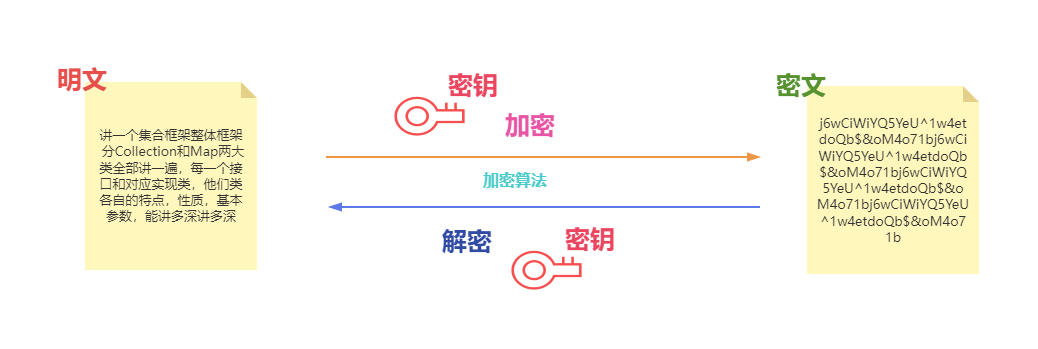
明文:加密前的消息叫“明文”(plain text)
密文:加密后的文本叫“密文”(cipher text)
密钥:只有掌握特殊“钥匙”的人,才能对加密的文本进行解密,这里的“钥匙”就叫做“密钥”(key)
“密钥”就是一个字符串,度量单位是“位”(bit),比如,密钥长度是128,就是16字节的二
进制串
加密:实现机密性最常用的手段是“加密”(encrypt)
按照密钥的使用方式,加密可以分为两大类:对称加密和非对称加密。
解密:使用密钥还原明文的过程叫“解密”(decrypt)
加密算法:加密解密的操作过程就是“加密算法”
所有的加密算法都是公开的,而算法使用的“密钥”则必须保密
2.对称和非对称加密
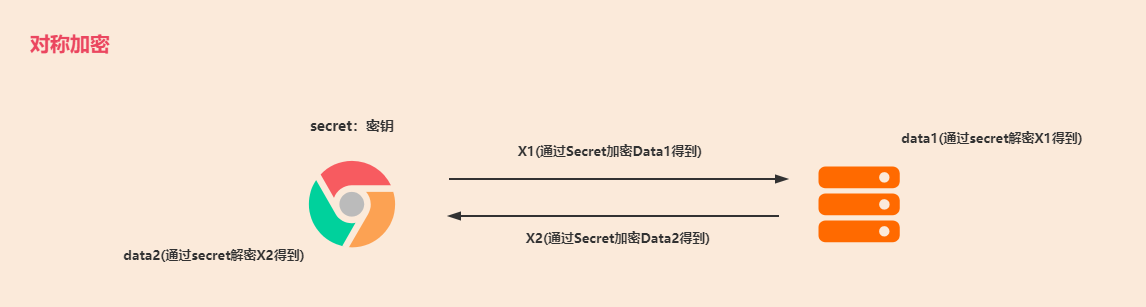
对称加密:
- 特点:只使用一个密钥,密钥必须保密,常用的有AES算法
- 优点:运算速度快
- 缺点:秘钥需要信息交换的双方共享,一旦被窃取,消息会被破解,无法做到安全的密钥交换
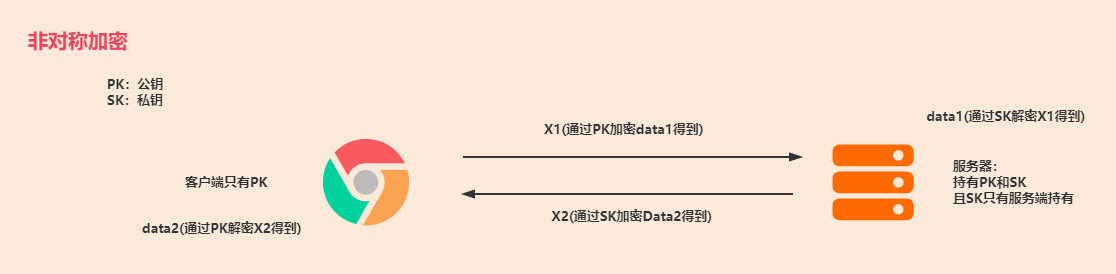
非对称加密:
- 特点:使用两个密钥:公钥和私钥,公钥可以任意分发而私钥保密,常用的有RSA
- 优点:黑客获取公钥无法破解密文,解决了密钥交换的问题
- 缺点:运算速度非常慢
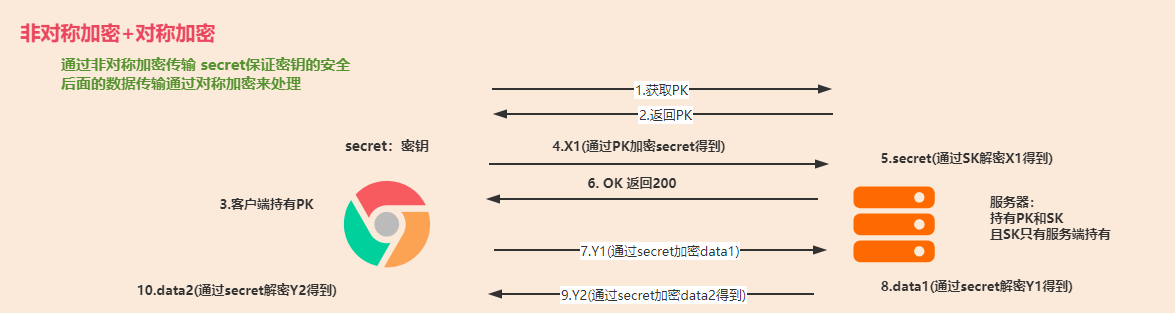
混合加密:
- 实际场景中把对称加密和非对称加密结合起来使用。
3.身份认证

公钥加密,私钥解密的作用是加密信息
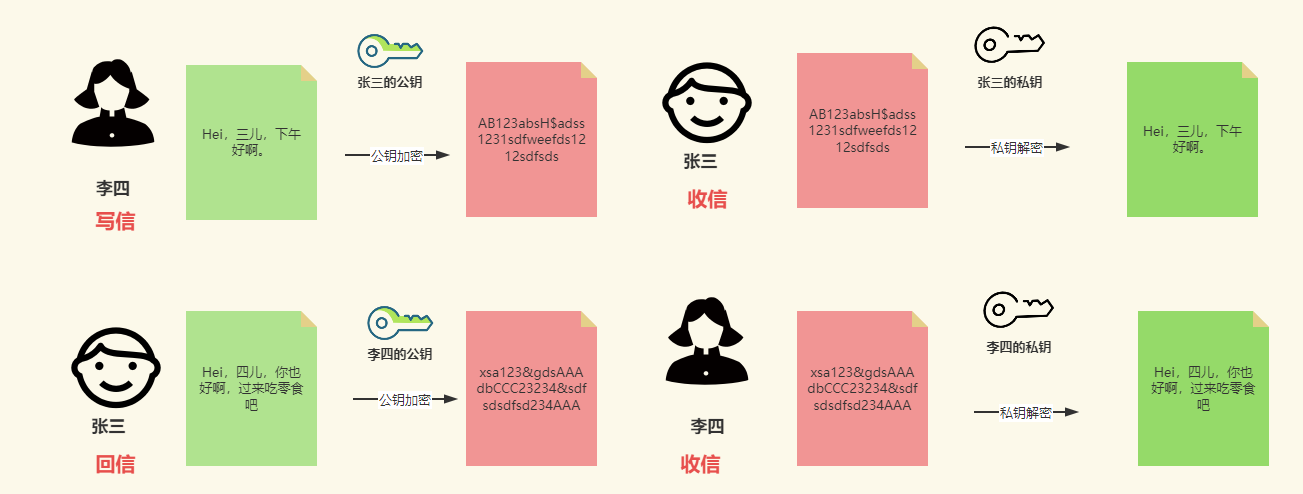
私钥加密,公钥解密的作用是身份认证
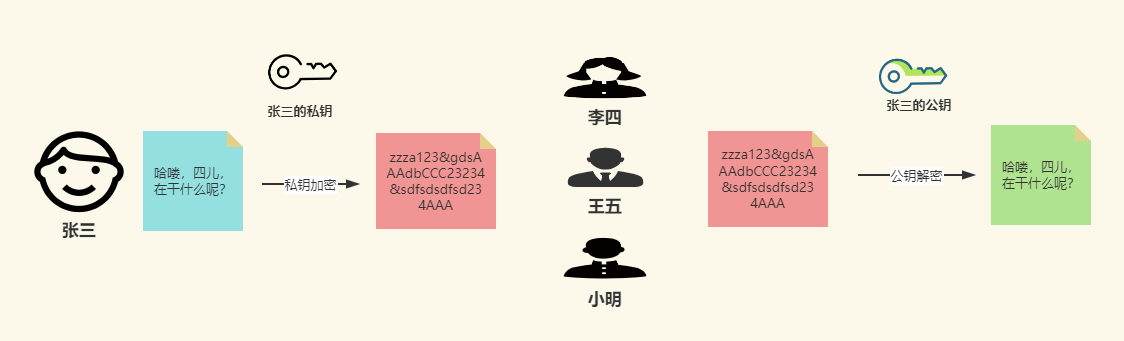
4.摘要算法
摘要算法就是我们常说的散列函数、哈希函数(Hash Function),它能够把任意长度的数据“压缩”成固定长度、而且独一无二的“摘要”字符串,就好像是给这段数据生成了一个数字“指纹”。

作用:
保证信息的完整性
特性:
- 不可逆:只有算法,没有秘钥,只能加密,不能解密
- 难题友好性:想要破解,只能暴力枚举
- 发散性:只要对原文进行一点点改动,摘要就会发生剧烈变化
- 抗碰撞性:原文不同,计算后的摘要也要不同
常见摘要算法:
MD5、SHA1、SHA2(SHA224、SHA256、SHA384)
举个简单例子:
public static void main(String[] args) {try {MessageDigest messageDigest = MessageDigest.getInstance("MD5");// 反复调用update输入数据:messageDigest.update("aa".getBytes(StandardCharsets.UTF_8));byte[] result = messageDigest.digest();System.out.println(new BigInteger(1, result).toString(16));} catch (NoSuchAlgorithmException e) {e.printStackTrace();}}
摘要算法的应用
- 下载软件校验
- 彩虹表问题
数据安全性:
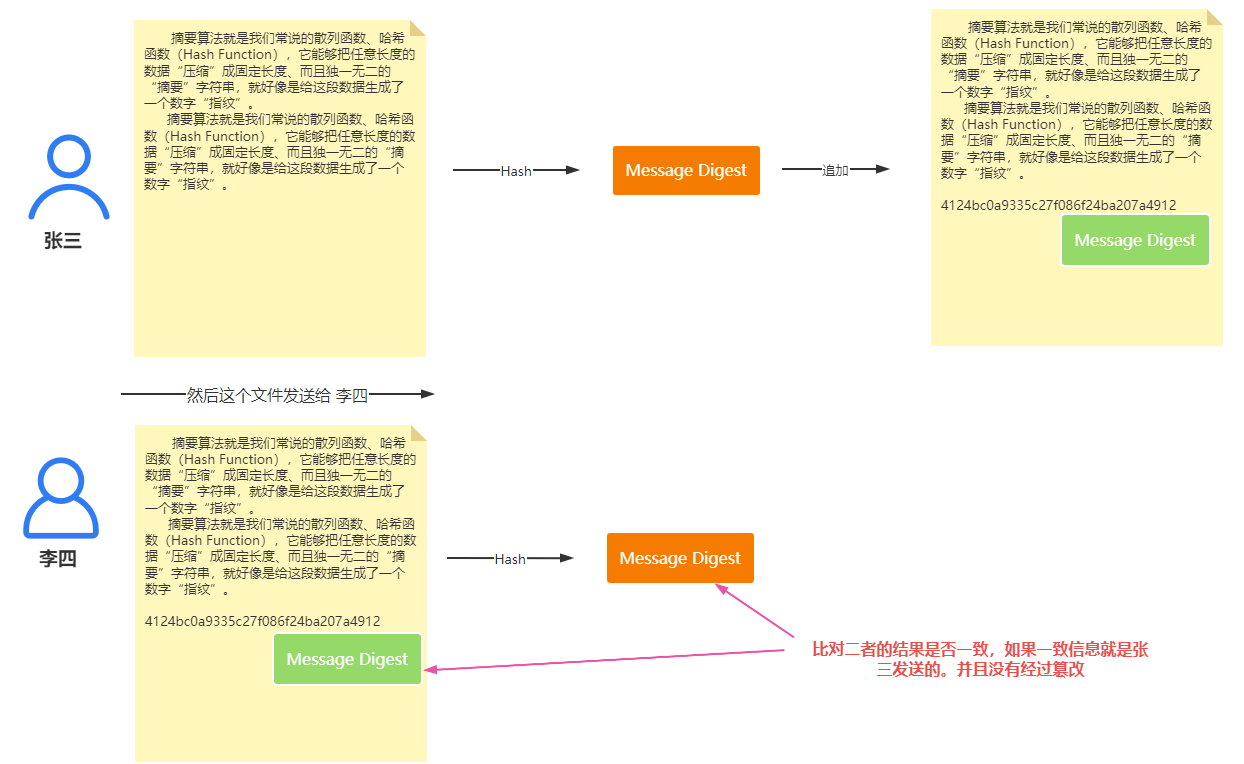
当然上面的操作也有问题的。如果黑客获取到了明文,然后修改内容后重新生成了摘要。替换了原来的摘要。然后把信息传递到了李四处,李四根据hash得到的摘要和传递的摘要比较发现是一样的。但是其实数据是已经修改过的了。这也就产生了数据安全问题。针对这个问题我们就需要通过数字签名来解决这个问题了。
数字签名
针对上面的问题,我们可以对生成的摘要通过私钥加密处理。然后拼接在传递信息中。然后在服务器中根据公钥解密得到的摘要和正常的明文hash后的摘要信息比较是否相同,如果相同就认为是正确的。
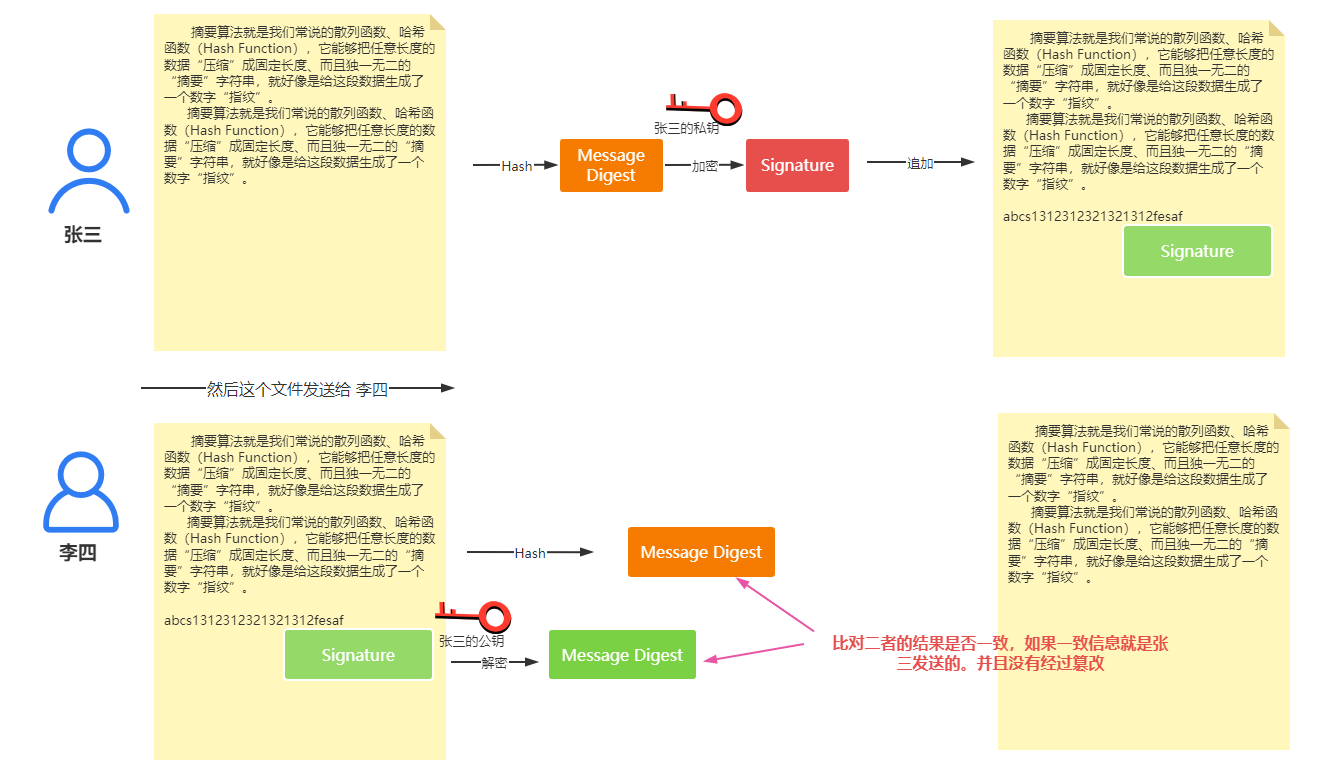
上面的处理中。细心的小伙伴会发现其实公钥是很容易获取的,黑客伪造了公钥,然后你又从伪造网站获取到了公钥。这时就有问题了。
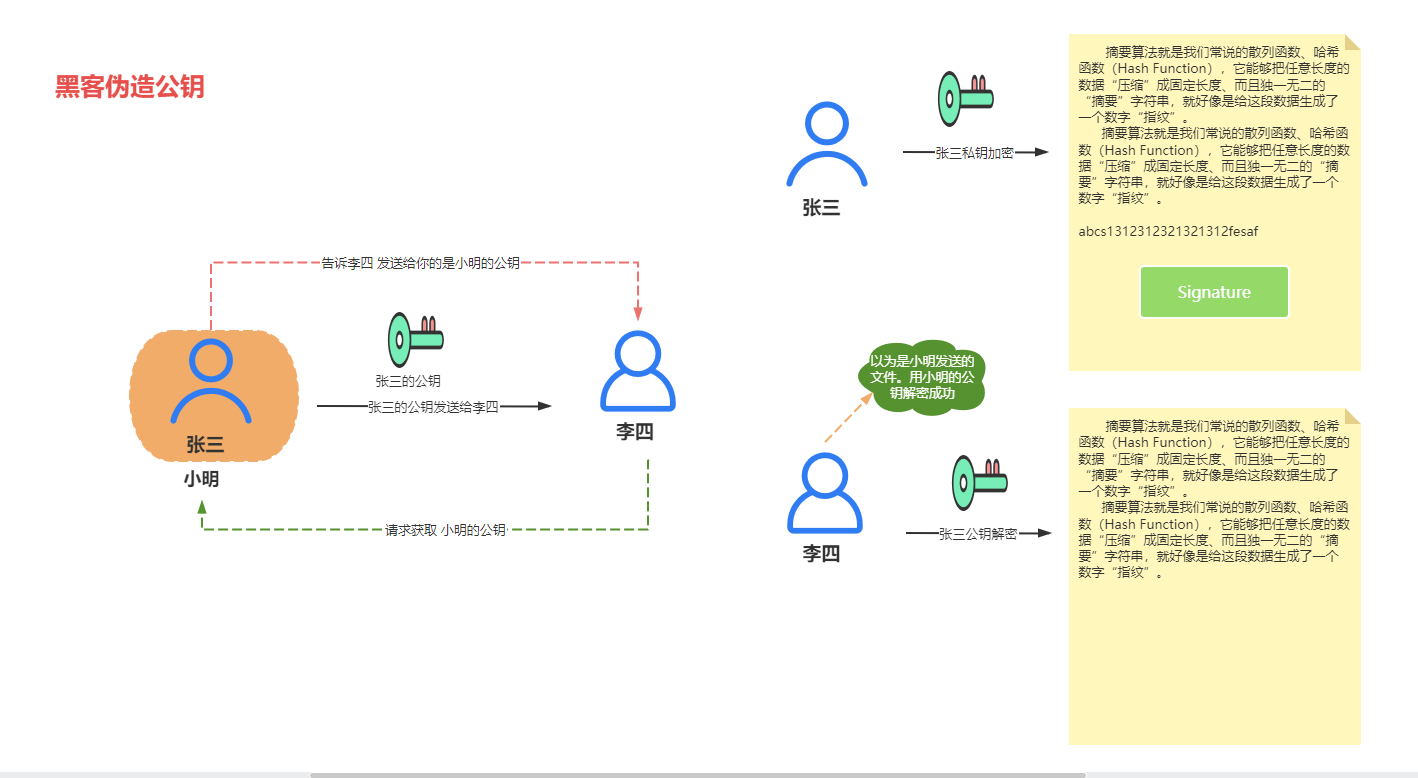
数字证书:
数字证书解决“公钥的信任”问题,可以防止黑客伪造公钥。不能直接分发公钥,公钥的分发必须使用数字证书,数字证书由CA颁发.
CA:证书认证机构

服务器向CA申请数字证书:需要提交相关的信息给CA机构。然后CA机构通过如下操作生成数字证书返回给你申请者
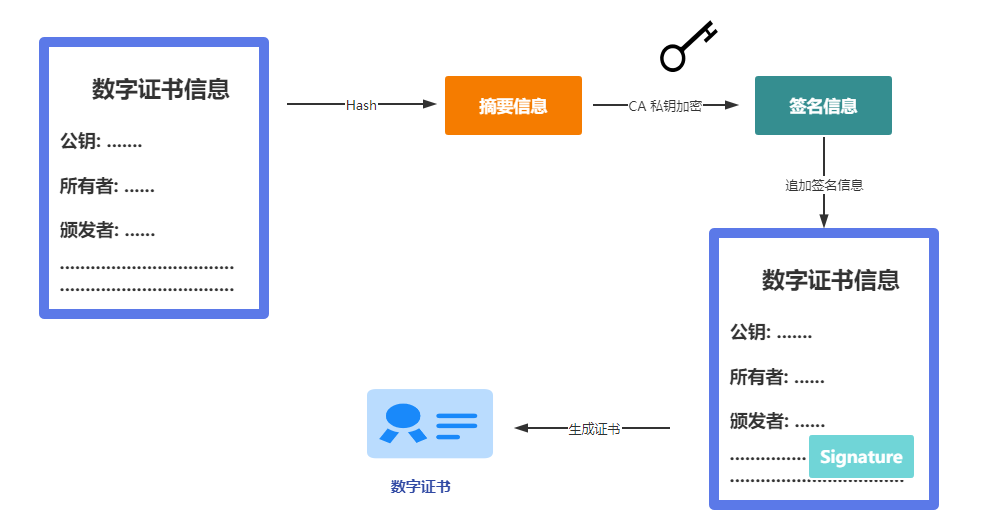
在这个数字证书中包含的有申请者的公钥信息。然后申请者在传输信息时就会携带改数字证书。

完整的处理流程:
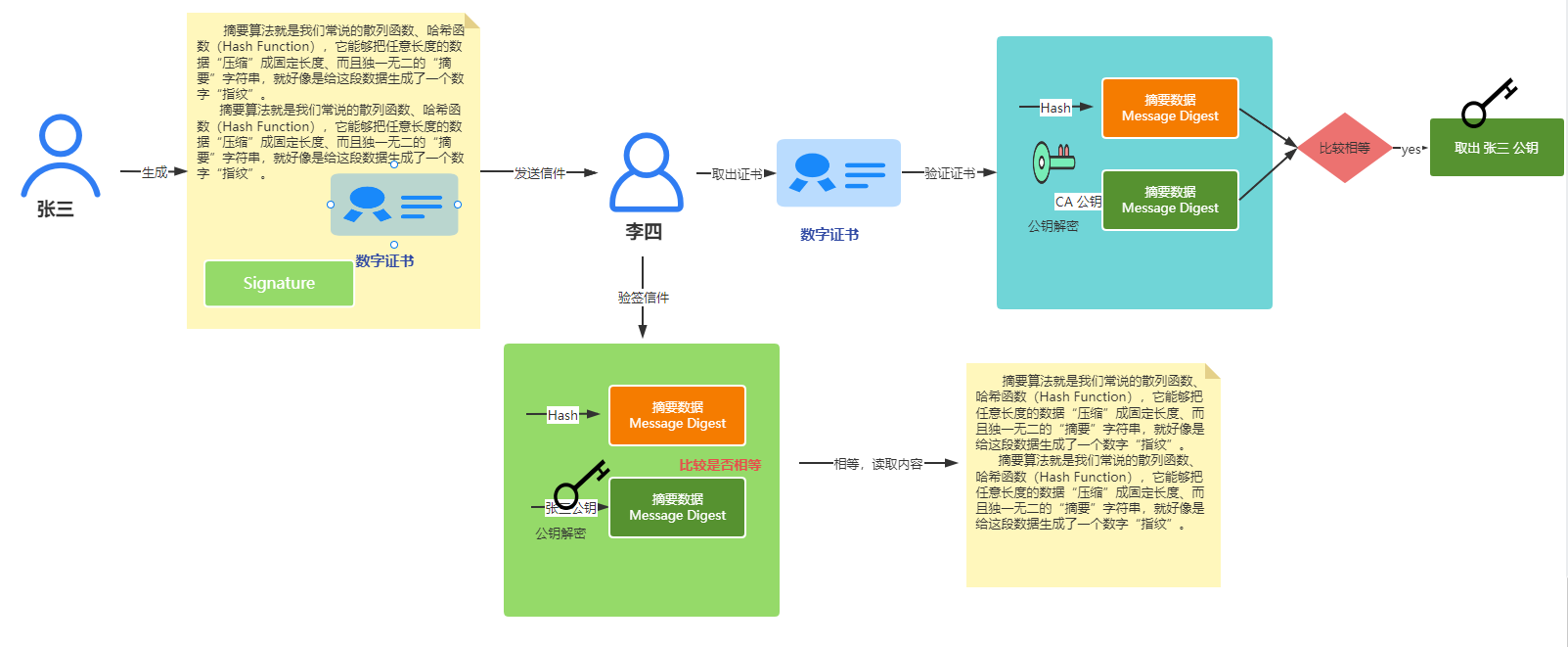 数字证书案例-----https协议
数字证书案例-----https协议
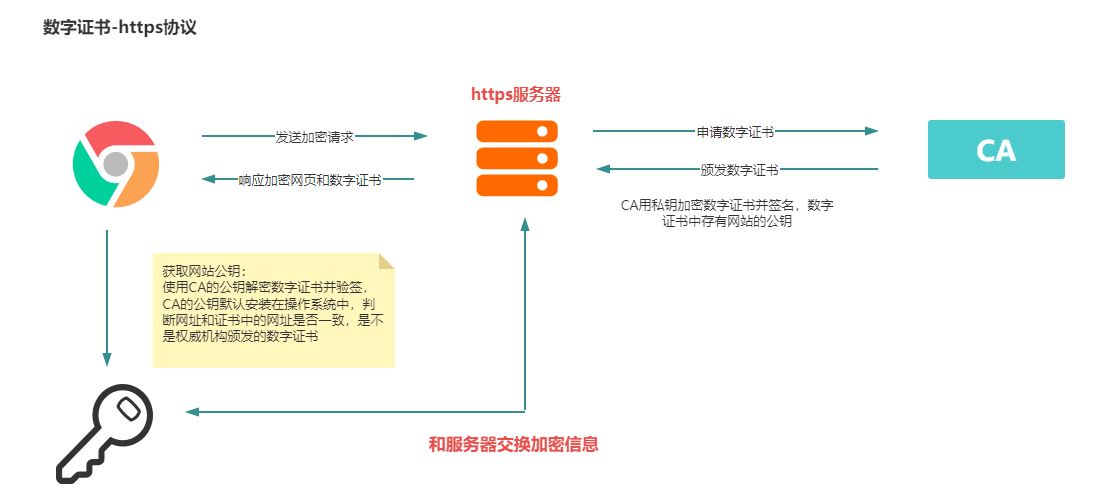
这篇关于如何保证数据的安全?对称和非对称加密,身份认证,摘要算法,数字证书等傻傻分不清?波哥图解带你彻底掌握的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








