【数据结构】树与二叉树（一）：树（森林）的基本概念：父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度

本文主要是介绍【数据结构】树与二叉树（一）：树（森林）的基本概念：父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

5.1 树的基本概念

5.1.1 树的定义

树

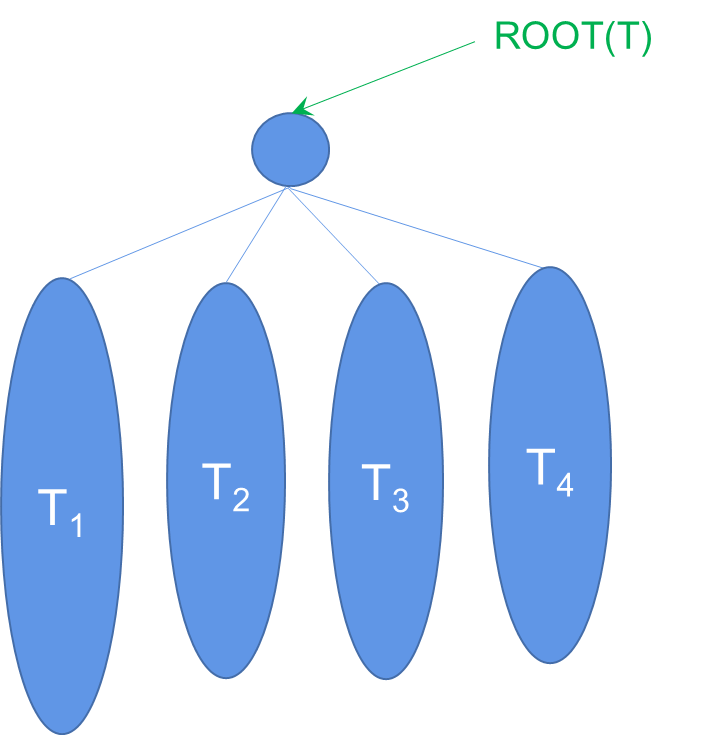
• 一棵树是结点的有限集合T：
  • 若T非空，则：
    • 有一个特别标出的结点，称作该树的根，记为root(T)；
    • 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0)，其中T1, T2, …, Tm又都是树，称作root(T)的子树。
      • 
  • T 空时为空树，记作root(T)=NULL。

有序树、无序树

  如果子树T1, T2, …, Tm 的相对次序被指明，则称该树为有序树，否则称为无序树。
  在有序树中，把Ti (1≤i≤m)称作根的第 i 个子树。因为计算机表示定义了树的一种隐含次序，所以大多数情况下假定所讨论的树都是有序的，除非另有说明。

• 如果是有序树，那么两者是不同的；如果是无序树，那么两者是相同的。
  

5.1.2 森林的定义

  一个森林是0棵或多棵不相交（非空）树的集合，通常是一个有序的集合。换句话说，森林由多个树组成，这些树之间没有交集，且可以按照一定的次序排列。在森林中，每棵树都是独立的，具有根节点和子树，树与树之间没有直接的连接关系。
  森林是树的扩展概念，它是由多个树组成的集合。在计算机科学中，森林也被广泛应用于数据结构和算法设计中，特别是在图论和网络分析等领域。

5.1.3 树的术语

1. 父亲（parent）、儿子（child）、兄弟（sibling）、后裔（descendant）、祖先（ancestor）

• 这些术语用于描述节点之间的关系和层次结构：

  • 每个节点都是它的子树的根节点的父亲。
  • 反过来，每个节点都是它父亲的儿子。
  • 具有相同父亲的节点称为兄弟。
  • 每个节点都是它子树中所有节点的祖先。
  • 反过来，每个节点都是它祖先的后裔。

• 节点之间的父子关系和兄弟关系可以帮助我们理解树的结构和遍历算法。

• 祖先和后裔的概念则用于描述节点之间的历史关系和衍生关系。

2. 度（degree）、叶子节点（leaf node）、分支节点（internal node）

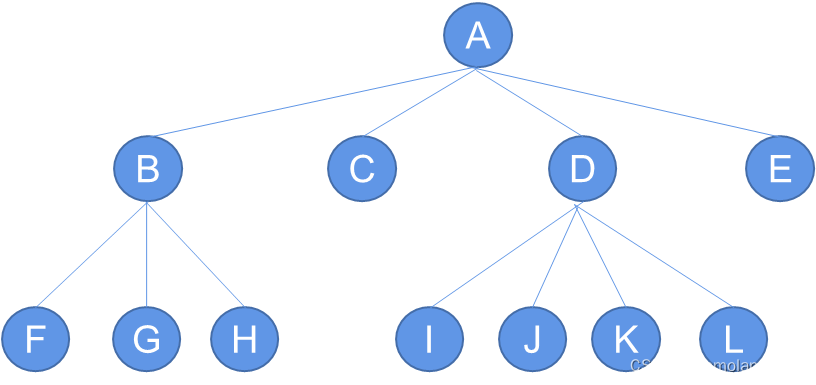
• 一个节点的儿子的个数称为该节点的度或次数。
• 如果一个节点的度为0，则它被称为终端节点或叶子节点（在严格意义上，非根的终端节点称为叶子节点）。
• 非终端节点称为分支节点。

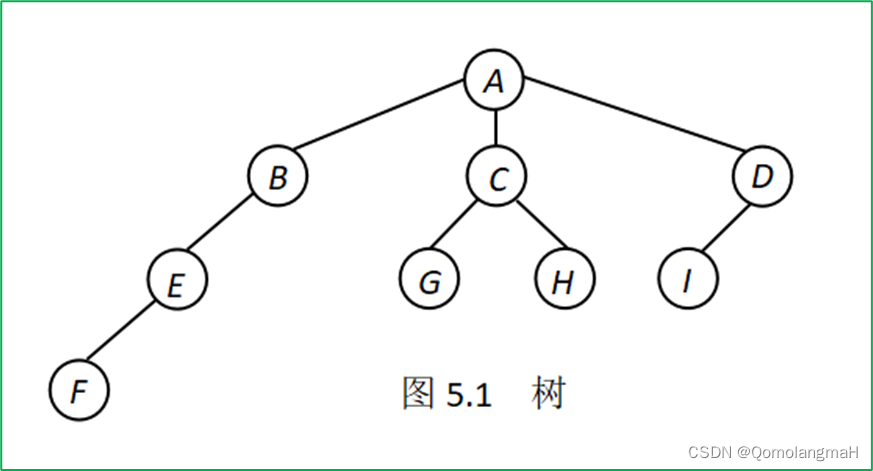
  在图5.1中，节点B有一个子树，其度为1；节点A有三个子树，其度为3；因此，这棵树的度为3，可以称为3元树（3-ary tree）。叶子节点是度为0的节点，例如在图5.1中，节点F、G、H和I是叶子节点，而节点A、B、C、D和E是分支节点。

3. 结点的层数

• 结点的层数是根据递归定义来确定的：
  • 根节点的层数为0。
  • 其余节点的层数是其父节点的层数加1。
• 根节点位于第0层，它的子节点位于第1层，子节点的子节点位于第2层，依此类推。
  

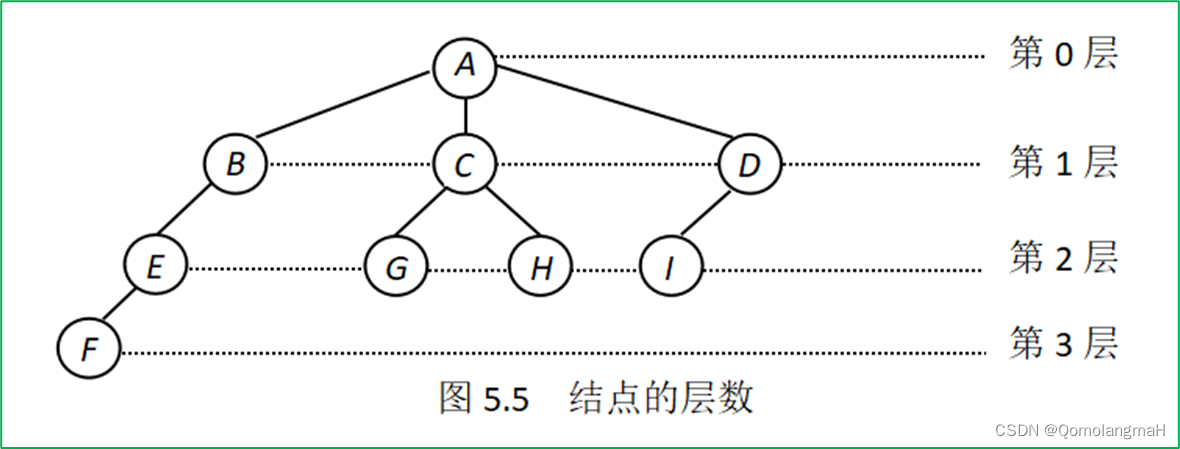
4. 路径、路径长度、结点的深度、树的深度

• 路径是指结点序列v1, v2, …, vk，其中每个节点vi是节点vi+1的父节点（1 ≤ i < k）。
• 路径长度是指路径经过的边数，即k-1。
• 结点vi的深度是指从根节点到结点vi的路径长度$Depth(i)$。
• 一棵树的深度是指树中所有节点深度的最大值：$ma{x}_{i=1,\dots ,n}Depth(i)$

  图5.1的树中，结点序列A, B, E是结点A到结点E的路径，路经长度为2，结点E的深度为2，树的深度为3。

5.1.4 树的表示

1．树形表示法

class TreeNode:def __init__(self, value):self.value = valueself.children = []# 创建一个树
root = TreeNode('A')
node1 = TreeNode('B')
node2 = TreeNode('C')
node3 = TreeNode('D')root.children.append(node1)
root.children.append(node2)
node2.children.append(node3)

2．嵌套集合表示法

tree = {'value': 'A','children': [{'value': 'B','children': []},{'value': 'C','children': [{'value': 'D','children': []}]}]
}

3．嵌套括号表示法

tree_str = '((A (B C)) D)'

4．凹入表示法

def print_tree(node, level=0):if node is None:returnprint('  ' * level + str(node.value))for child in node.children:print_tree(child, level + 1)print_tree(root)

这篇关于【数据结构】树与二叉树（一）：树（森林）的基本概念：父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---