本文主要是介绍Nelder-Mead算法(智能优化之下山单纯形法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Nelder-Mead 算法是一种求多元函数局部最小值的算法,其优点是不需要函数可导并能较快收敛到局部最小值。
该算法需要提供函数自变量空间中的一个初始点x1,算法从该点出发寻找局部最小值
Nelder-Mead方法也称下山单纯形法,是由John Nelder & Roger Mead于1965年提出的一种求解数值优化问题的启发式搜索
给定n+1个顶点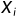 (i=1,2...,n+1),这些点对应的函数值为
(i=1,2...,n+1),这些点对应的函数值为
开始按以下算法步骤进行,直到满足特定的精度条件或者循环次数时退出循环:
一、按照目标函数值对n+1个点进行从好到差排序,确定最坏点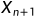 ,第二最坏点
,第二最坏点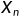 和最好点
和最好点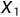
二、计算除去最差点外其他点的中心点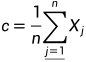
三、反射操作,计算反射点 (
(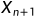 就是最坏的点,C是第二步计算出的中心点,
就是最坏的点,C是第二步计算出的中心点, 是反射系数,等于1)
是反射系数,等于1)
3.1若
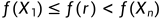 (意思是反射点的结果在最好点和第二差点之间)令
(意思是反射点的结果在最好点和第二差点之间)令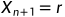 (也 就是去掉了最坏点),并进入下一层循环。
(也 就是去掉了最坏点),并进入下一层循环。
3.2若
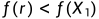 (意思是反射点的结果比最好的点还要好),计算拓展点
(意思是反射点的结果比最好的点还要好),计算拓展点
3.2.1若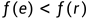 (意思是扩展点得到的结果比反射点要好),令
(意思是扩展点得到的结果比反射点要好),令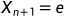 ,并进入下一 层循环
,并进入下一 层循环
3.2.2否则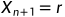 (扩展失败的意思),进入下一层循环
(扩展失败的意思),进入下一层循环
3.3若
 (意思是反射点的结果在最差点和第二差点之间且比最差点要 好)此时进行向外压缩操作,计算
(意思是反射点的结果在最差点和第二差点之间且比最差点要 好)此时进行向外压缩操作,计算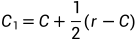
3.3.1若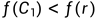 (意思是向外压缩点比反射点结果要好),令
(意思是向外压缩点比反射点结果要好),令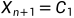 (替换掉最 差点),并进入下一层循环
(替换掉最 差点),并进入下一层循环
3.3.2否则执行最后一步
3.4若
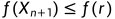 (意思是反射点的结果比最差点还要糟糕),此时进行向内压缩操作,计算
(意思是反射点的结果比最差点还要糟糕),此时进行向内压缩操作,计算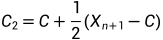
3.4.1若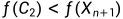 ,令
,令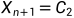 ,并进入下一层循环
,并进入下一层循环
3.4.2否则进入下一层循环
3.5若上述四个条件都不符合,则令
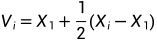 (i=2,...n+1),并且将
(i=2,...n+1),并且将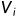 赋值给
赋值给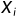 并进入下一层循环
并进入下一层循环
下面以二元函数 为例,使用python编程
为例,使用python编程
给定初始点:[0,0],[1.2,0],[0,0.8]
def func(x1, x2):return x1 * x1 - 4 * x1 + x2 * x2 - x2 - x1 * x2# 创建一个简单的二维数组
x = [[0, 0, 0], [1.2, 0, 0], [0, 0.8, 0]]
n = len(x)
m=0
for m in range(20):# 第一步,将这些点按照从小到大排序# 计算每个点对应的函数值for i in range(n):x[i][2] = func(x[i][0], x[i][1])# 按照目标函数值进行排序---从小到大排序for i in range(n - 1):for j in range(n - 1):if x[j][2] > x[j + 1][2]:temp = x[j]x[j] = x[j + 1]x[j + 1] = tempprint("第{}次循环得到的最优值为:".format(m),x[0])# 第二步,计算除去最坏点的其他点的中心点c = [0, 0, 0] # 进行一个初始化c[0] = (x[0][0] + x[1][0]) / 2c[1] = (x[0][1] + x[1][1]) / 2c[2] = func(c[0], c[1])# 第三步进行反射操作,计算反射点xr = [0, 0, 0]xr[0] = 2 * c[0] - x[2][0]xr[1] = 2 * c[1] - x[2][1]xr[2] = func(xr[0], xr[1])if x[0][2] <= xr[2] < x[1][2]:x[2] = xrcontinueelif xr[2] < x[0][2]:xe = [0, 0, 0]xe[0] = 3 * c[0] - 2 * x[2][0]xe[1] = 3 * c[1] - 2 * x[2][1]xe[2] = func(xe[0], xe[1])if xe[2] < xr[2]:x[2] = xecontinueelse:x[2] = xrcontinueelif x[1][2] <= xr[2] < x[2][2]:c1 = [0, 0, 0]c1[0] = c[0] + (xr[0] - c[0]) / 2c1[1] = c[1] + (xr[1] - c[1]) / 2c1[2] = func(c1[0], c1[1])if c1[2] < xr[2]:x[2] = c1continueelse:passelif x[2][2] <= xr[2]:c2 = [0, 0, 0]c2[0] = c[0] + (x[2][0] - c[0])c2[1] = c[1] + (x[2][1] - c[1])c2[2]=func(c2[0],c2[1])if c2[2]<x[2][2]:x[2]=c2continueelse:passi=1for i in range(n):x[i][0]=x[0][0]+(x[i][0]-x[0][0])/2x[i][1] = x[0][1] + (x[i][1] - x[0][1]) / 2x[i][2]=func(x[i][0],x[i][1])continue运行结果如下图所示:
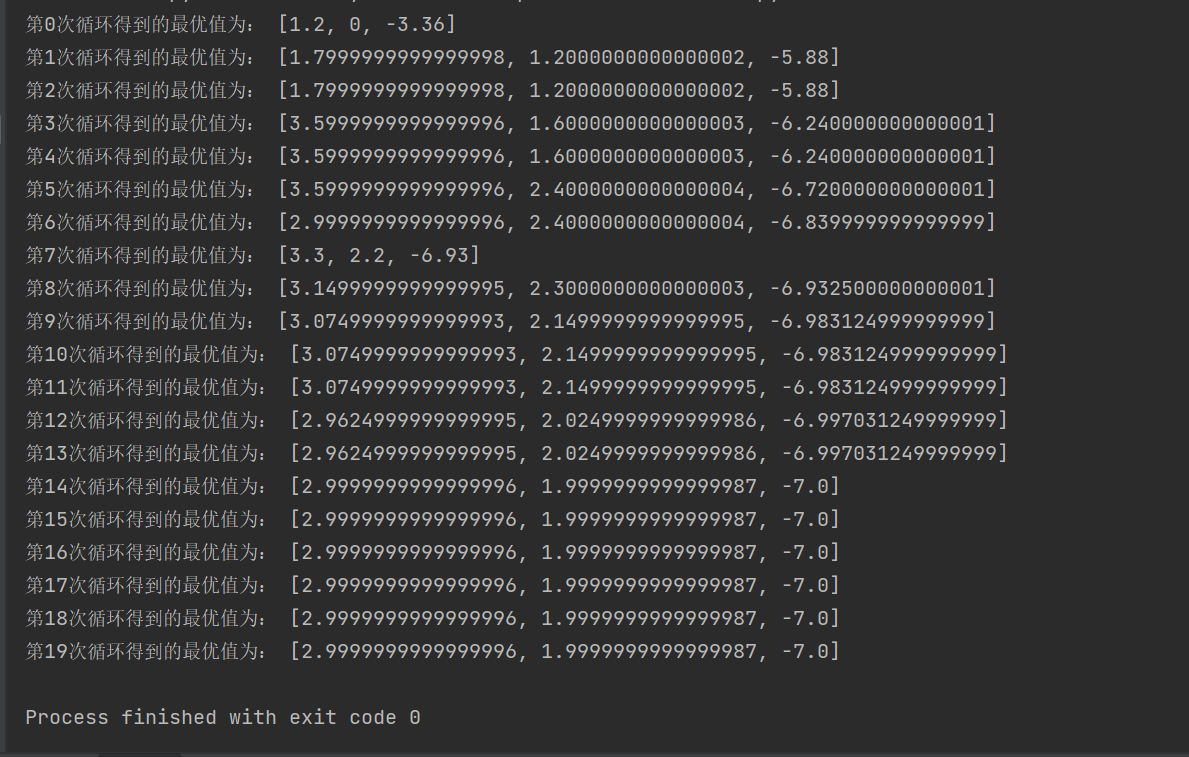
这篇关于Nelder-Mead算法(智能优化之下山单纯形法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



