彻底搞懂克鲁斯卡尔（Kruskal）算法（附C++代码实现）

本文主要是介绍彻底搞懂克鲁斯卡尔（Kruskal）算法（附C++代码实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一.问题

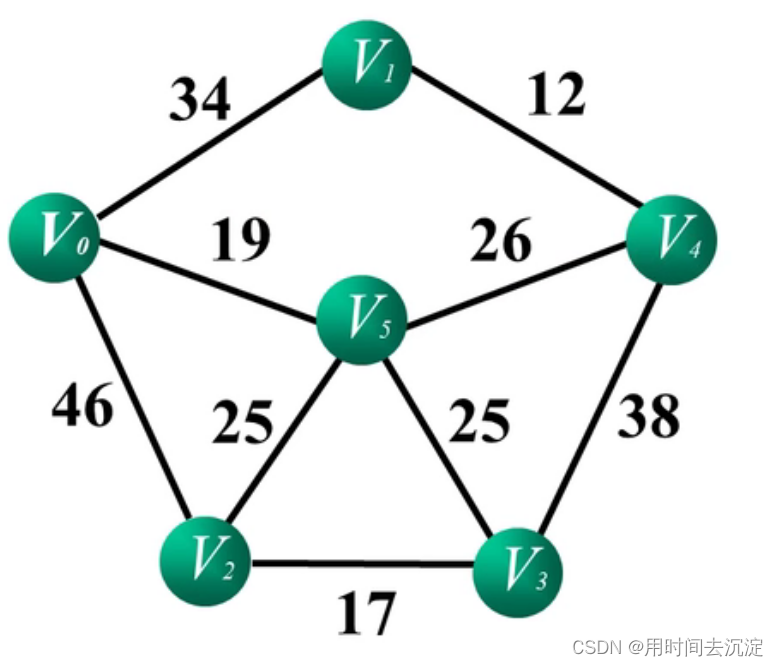
图中的6个顶点分别代表6个村庄，线段的权值代表村庄之间的距离。请问如何找到最短的路径来访问每一个村庄，且每个村庄只访问一次。

二.解决

1.提取图的边，并将边按权值大小从小到大排列，并放入edge数组。如下：

2.创建根数组（辅助数组），数组下标代表顶点节点本身，其元素代表顶点的根节点，如下：

提示：这里的“根”并不是树结构中真正的根，一棵树中只有一个根，而这里的“根”泛指长辈，可能是父节点，也可能是“爷”节点。初始化根数组为-1，代表初始状态下每个顶点都各自代表一个集合。

3.将edge数组中的边从小到大依次放回图中，如果后续加入的边与图中已放入的边形成了环，那么将此边丢弃，继续将下一条边放入，规则同前。

形成环，即说明加入的这条边的起点和终点已经属于一个集合，有共同的根。加入边的过程就是多个子集不断合并的过程，同一集合中的顶点不可相连。前面的辅助数组就是用来判断起点与终点是否属于一个集合。具体实现看代码注释。

4.放入（顶点数-1）条边后，最小生成树（Minimum Spanning Tree）构建完成，即可结束循环。

一棵树有n个节点，则有n-1条边

三.细节

上述算法主要有两点需要考虑：

树的储存
集合的表示

树的储存：常见的图储存结构有：邻接矩阵,邻接边表,十字链表,邻接多重表,边集数组显然，上述算法中频繁涉及到对边的操作，所以边集数组是最佳选择。

集合的表示：使用辅助数组，存放各顶点的根顶点，如果两个顶点的根相同，则属于同一集合，另则相反。初始化辅助数组元素为-1，代表每个顶点本身就是根节点。

四.实现

#include<iostream>
#define MAX_VEX  10
#define MAX_EDGE 100  //10个顶点组成的无向图最多有100条边
#define TYPE int
using namespace std;struct Edge  //边的属性结构体
{TYPE start;TYPE end;TYPE weight;
};void ini_gragh(int& vex, int& edge, Edge* gragh);//采用边集数组储存图void sort_edge(Edge* edges,int edge);//使用冒泡排序，根据权值大小将边从小到大排序int find_root(int parent[], int n);//寻找根节点以判断是否在一个集合中int main()
{int vex; //顶点个数int edge; //边个数Edge gragh[MAX_EDGE];ini_gragh(vex, edge, gragh);//边集数组初始化图sort_edge(gragh, edge);//依据权值大小给边从小到大排序int roots[MAX_VEX];  //根数组，存放各顶点的根节点，以区别是否属于同一个集合Edge MST[MAX_EDGE];   //存放最小生成树（minimum spanning tree）int count = 0;  for (int i = 0; i < vex; i++)roots[i] = -1;  //初始化root数组，-1代表自己就是根节点；初始状态下每个顶点都是独立的根for (int i = 0; i < MAX_EDGE; i++){int vex_m = find_root(roots, gragh[i].start);//寻找起点的根节点int vex_n = find_root(roots, gragh[i].end);//寻找终点的根节点if (vex_m != vex_n)//如果两者的根节点不同，说明他们属于不同的集合，可以相连{MST[count] = gragh[i];//将此边放入MST数组count++;roots[vex_m] = vex_n;//将两个树合并，即将顶点vex_n作为vex_m的根节点}if (count == vex-1)//当count达到顶点数-1，说明最小树已经生成，退出循环break;}for (int i = 0; i < vex - 1; i++){printf("(%d,%d)%d\n", MST[i].start, MST[i].end, MST[i].weight);   //打印最小生成树}return 0;
}void ini_gragh(int& vex, int& edge, Edge* gragh)
{cout << "输入连通网顶点数：";cin >> vex;cout << "输入连通网边数： ";cin >> edge;cout << "依次输入各边的起点，终点和权重(空格隔开)：" << endl;for (int i = 0; i < edge; i++){cin >> gragh[i].start >> gragh[i].end >> gragh[i].weight;}
}void sort_edge(Edge* edges_arr,int edge)
{Edge temp;	for (int i = 0; i < edge; i++){for (int k = 0; k < edge - i - 1; k++)//冒泡排序，注意这里要减1{if (edges_arr[k].weight > edges_arr[k + 1].weight){temp = edges_arr[k];edges_arr[k] = edges_arr[k + 1];edges_arr[k + 1] = temp;}}}
}int find_root(int roots[], int n)
{while (roots[n] > -1)  //迭代寻找根节点n = roots[n];return n;
}

运行结果：