自学SLAM（7）非线性优化实践：曲线拟合问题（使用ceres库和SLAM常用的g2o库）

2023-11-04 22:36
文章标签 自学 问题 使用 实践 优化 slam 常用 非线性 ceres g2o 曲线拟合

本文主要是介绍自学SLAM（7）非线性优化实践：曲线拟合问题（使用ceres库和SLAM常用的g2o库），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

在这里插入图片描述

本次文章针对的是第四个视屏中的实践问题

肯定会有部分方法没有说到，比如高斯牛顿法，后面我会把此次视屏对应的作业写好，然后补充到此次博客！！

文章目录

  • 前言
  • 1.曲线拟合题目：
  • 2.非线性最小二乘
    • 2.1 黄金分割法(0.618法)
    • 2.2 最速下降法
  • 3.ceres库实现曲线拟合题目
    • 3.1 安装ceres
    • 3.2 代码及运行
  • 4.g2o库实现曲线拟合题目
    • 4.1 安装g2o
    • 4.2 代码及运行

1.曲线拟合题目：

设有曲线满⾜以下⽅程：
y = exp(ax2 + bx + c) + w
其中 a; b; c 为曲线参数， w 为噪声。现有 N个数据点 (x, y)，希望通过此 N 个点来拟合 a; b; c。实验中取N = 100。那么，定义误差为 ei = yi −exp(ax2 i + bxi + c)，于是 (a，b， c)的最优解可通过解以下最⼩⼆乘获得：在这里插入图片描述

使用ceres库和g2o库完成该题目

2.非线性最小二乘

![在这里插入图片描述](https://img-blog.csdnimg.cn/42930a0b98ce46b1b2ab40eb3f0c0d1

这里涉及到很多非线性优化的知识，如果你对这些知识没有概念，一定要去中国最好的大学——哔哩哔哩大学先自学一下，什么是凸函数，凸规划，海塞矩阵，黄金分割法(0.618法)，最速下降法，牛顿法，高斯牛顿法等等，否则这一块的知识你将无法理解！！！！

我会对某些方法做一些简单的说明：

在这里插入图片描述

2.1 黄金分割法(0.618法)

在这里插入图片描述

2.2 最速下降法

在这里插入图片描述

3.ceres库实现曲线拟合题目

Ceres库来自谷歌。是一个广泛使用的最小二乘问题求解库。

最小二乘问题：最小化观测数据的高维高斯分布形式的误差的平方，就可以得到最优的位姿状态。对于不方便求解的最小二乘问题，可以用迭代的方式，从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。此时，只要找到迭代点的梯度方向即可，而无须寻找全局导函数为零的情况。（这个和神经网络里面的梯度下降方式一样欸！殊途同归的感觉）
在这里插入图片描述

3.1 安装ceres

//安装依赖项
sudo apt-get install liblapack-dev libsuitesparse-dev libgflags-dev 
sudo apt-get install libgoogle-glog-dev libgtest-dev
sudo apt-get install libcxsparse3wget ceres-solver.org/ceres-solver-1.14.0.tar.gz//下载后解压//安装
cd ceres-solver-1.14.0
sudo mkdir build
cd build
cmake ..
make
sudo make install

3.2 代码及运行

main.cpp:

#include <iostream>
#include <opencv2/core/core.hpp>
#include <ceres/ceres.h>
#include <chrono>using namespace std;// 代价函数的计算模型
struct CURVE_FITTING_COST
{CURVE_FITTING_COST ( double x, double y ) : _x ( x ), _y ( y ) {}// 残差的计算template <typename T>bool operator() (const T* const abc,     // 模型参数，有3维T* residual ) const     // 残差{residual[0] = T ( _y ) - ceres::exp ( abc[0]*T ( _x ) *T ( _x ) + abc[1]*T ( _x ) + abc[2] ); // y-exp(ax^2+bx+c)return true;}const double _x, _y;    // x,y数据
};int main ( int argc, char** argv )
{double a=1.0, b=2.0, c=1.0;         // 真实参数值int N=100;                          // 数据点double w_sigma=1.0;                 // 噪声Sigma值cv::RNG rng;                        // OpenCV随机数产生器double abc[3] = {0,0,0};            // abc参数的估计值vector<double> x_data, y_data;      // 数据cout<<"generating data: "<<endl;for ( int i=0; i<N; i++ ){double x = i/100.0;x_data.push_back ( x );y_data.push_back (exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma ));cout<<x_data[i]<<" "<<y_data[i]<<endl;}// 构建最小二乘问题ceres::Problem problem;for ( int i=0; i<N; i++ ){problem.AddResidualBlock (     // 向问题中添加误差项// 使用自动求导，模板参数：误差类型，输出维度，输入维度，维数要与前面struct中一致new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3> ( new CURVE_FITTING_COST ( x_data[i], y_data[i] )),nullptr,            // 核函数，这里不使用，为空abc                 // 待估计参数);}// 配置求解器ceres::Solver::Options options;     // 这里有很多配置项可以填options.linear_solver_type = ceres::DENSE_QR;  // 增量方程如何求解options.minimizer_progress_to_stdout = true;   // 输出到coutceres::Solver::Summary summary;                // 优化信息chrono::steady_clock::time_point t1 = chrono::steady_clock::now();ceres::Solve ( options, &problem, &summary );  // 开始优化chrono::steady_clock::time_point t2 = chrono::steady_clock::now();chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;// 输出结果cout<<summary.BriefReport() <<endl;cout<<"estimated a,b,c = ";for ( auto a:abc ) cout<<a<<" ";cout<<endl;return 0;
}

CMakeLists.txt:

cmake_minimum_required( VERSION 2.8 )
project( ceres_curve_fitting )set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )# 添加cmake模块以使用ceres库
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )# 寻找Ceres库并添加它的头文件
find_package( Ceres REQUIRED )
include_directories( ${CERES_INCLUDE_DIRS} )# OpenCV
find_package( OpenCV REQUIRED )
include_directories( ${OpenCV_DIRS} )add_executable( curve_fitting main.cpp )
# 与Ceres和OpenCV链接
target_link_libraries( curve_fitting ${CERES_LIBRARIES} ${OpenCV_LIBS} )

运行：

cd ceres_curve_fitting
mkdir build
cd build
cmake ..
make
./curve_fitting

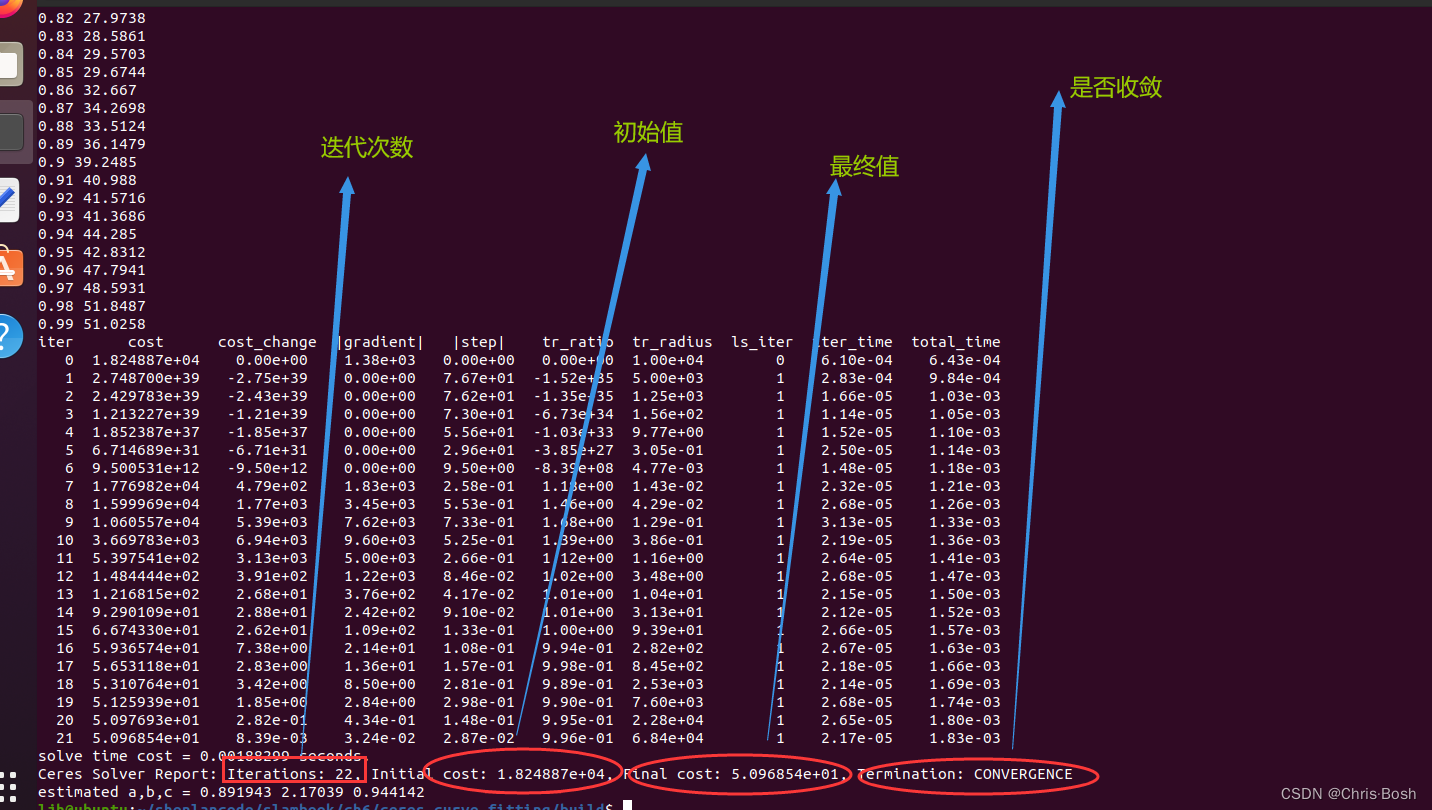
在这里插入图片描述

最后一行是估计值，估计值的准确度取决于噪音，也就是代码中(main.cpp)的 w_sigma,噪声越小越接近于实际值a=1，b=2，c=1

4.g2o库实现曲线拟合题目

4.1 安装g2o

这个必须用高博再3rdparty中给的，不然后面会一直出错!

//依赖项
sudo apt-get install libeigen3-dev
sudo apt-get install libsuitesparse-dev
sudo apt-get install qtdeclarative5-dev
sudo apt-get install qt5-qmake
sudo apt-get install libqglviewer-dev
//安装
cd g2o
mkdir build
cd build
sudo ldconfig
cmake ..
make
sudo make install

4.2 代码及运行

main.cpp:

#include <iostream>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <Eigen/Core>
#include <opencv2/core/core.hpp>
#include <cmath>
#include <chrono>
using namespace std; // 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWvirtual void setToOriginImpl() // 重置{_estimate << 0,0,0;}virtual void oplusImpl( const double* update ) // 更新{_estimate += Eigen::Vector3d(update);}// 存盘和读盘：留空virtual bool read( istream& in ) {}virtual bool write( ostream& out ) const {}
};// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWCurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}// 计算曲线模型误差void computeError(){const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);const Eigen::Vector3d abc = v->estimate();_error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;}virtual bool read( istream& in ) {}virtual bool write( ostream& out ) const {}
public:double _x;  // x 值， y 值为 _measurement
};int main( int argc, char** argv )
{double a=1.0, b=2.0, c=1.0;         // 真实参数值int N=100;                          // 数据点double w_sigma=1.0;                 // 噪声Sigma值cv::RNG rng;                        // OpenCV随机数产生器double abc[3] = {0,0,0};            // abc参数的估计值vector<double> x_data, y_data;      // 数据cout<<"generating data: "<<endl;for ( int i=0; i<N; i++ ){double x = i/100.0;x_data.push_back ( x );y_data.push_back (exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma ));cout<<x_data[i]<<" "<<y_data[i]<<endl;}// 构建图优化，先设定g2otypedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  // 每个误差项优化变量维度为3，误差值维度为1Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器// 梯度下降方法，从GN, LM, DogLeg 中选g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );g2o::SparseOptimizer optimizer;     // 图模型optimizer.setAlgorithm( solver );   // 设置求解器optimizer.setVerbose( true );       // 打开调试输出// 往图中增加顶点CurveFittingVertex* v = new CurveFittingVertex();v->setEstimate( Eigen::Vector3d(0,0,0) );v->setId(0);optimizer.addVertex( v );// 往图中增加边for ( int i=0; i<N; i++ ){CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );edge->setId(i);edge->setVertex( 0, v );                // 设置连接的顶点edge->setMeasurement( y_data[i] );      // 观测数值edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆optimizer.addEdge( edge );}// 执行优化cout<<"start optimization"<<endl;chrono::steady_clock::time_point t1 = chrono::steady_clock::now();optimizer.initializeOptimization();optimizer.optimize(100);chrono::steady_clock::time_point t2 = chrono::steady_clock::now();chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;// 输出优化值Eigen::Vector3d abc_estimate = v->estimate();cout<<"estimated model: "<<abc_estimate.transpose()<<endl;return 0;
}

CMakeLists.txt:

cmake_minimum_required( VERSION 2.8 )
project( g2o_curve_fitting )set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )# 添加cmake模块以使用ceres库
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )# 寻找G2O
find_package( G2O REQUIRED )
include_directories( ${G2O_INCLUDE_DIRS}"/usr/include/eigen3"
)# OpenCV
find_package( OpenCV REQUIRED )
include_directories( ${OpenCV_DIRS} )add_executable( curve_fitting main.cpp )
# 与G2O和OpenCV链接
target_link_libraries( curve_fitting ${OpenCV_LIBS}g2o_core g2o_stuff
)

运行：

cd g2o_curve_fitting
mkdir build
cd build
cmake ..
make
./curve_fitting

在这里插入图片描述
运行出的结果和ceres一样
在这里插入图片描述

这篇关于自学SLAM（7）非线性优化实践：曲线拟合问题（使用ceres库和SLAM常用的g2o库）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/345629。

相关文章

使用Python将JSON,XML和YAML数据写入Excel文件

使用Python将JSON,XML和YAML数据写入Excel文件

《使用Python将JSON,XML和YAML数据写入Excel文件》JSON、XML和YAML作为主流结构化数据格式,因其层次化表达能力和跨平台兼容性,已成为系统间数据交换的通用载体,本文将介绍如何... 目录如何使用python写入数据到Excel工作表用Python导入jsON数据到Excel工作表用
阅读更多...
Pyserial设置缓冲区大小失败的问题解决

Pyserial设置缓冲区大小失败的问题解决

《Pyserial设置缓冲区大小失败的问题解决》本文主要介绍了Pyserial设置缓冲区大小失败的问题解决,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面... 目录问题描述原因分析解决方案问题描述使用set_buffer_size()设置缓冲区大小后，buf
阅读更多...
resultMap如何处理复杂映射问题

resultMap如何处理复杂映射问题

《resultMap如何处理复杂映射问题》：本文主要介绍resultMap如何处理复杂映射问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录resultMap复杂映射问题Ⅰ 多对一查询：学生——老师Ⅱ 一对多查询：老师——学生总结resultMap复杂映射问题
阅读更多...
鸿蒙中@State的原理使用详解(HarmonyOS 5)

鸿蒙中@State的原理使用详解(HarmonyOS 5)

《鸿蒙中@State的原理使用详解(HarmonyOS5)》@State是HarmonyOSArkTS框架中用于管理组件状态的核心装饰器,其核心作用是实现数据驱动UI的响应式编程模式,本文给大家介绍... 目录一、@State在鸿蒙中是做什么的？二、@Spythontate的基本原理1. 依赖关系的收集2.
阅读更多...
Python基础语法中defaultdict的使用小结

Python基础语法中defaultdict的使用小结

《Python基础语法中defaultdict的使用小结》Python的defaultdict是collections模块中提供的一种特殊的字典类型,它与普通的字典（dict）有着相似的功能,本文主要... 目录示例1示例2python的defaultdict是collections模块中提供的一种特殊的字
阅读更多...
java实现延迟/超时/定时问题

java实现延迟/超时/定时问题

《java实现延迟/超时/定时问题》：本文主要介绍java实现延迟/超时/定时问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录Java实现延迟/超时/定时java 每间隔5秒执行一次,一共执行5次然后结束scheduleAtFixedRate 和 schedu
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
Java String字符串的常用使用方法

Java String字符串的常用使用方法

《JavaString字符串的常用使用方法》String是JDK提供的一个类,是引用类型,并不是基本的数据类型,String用于字符串操作,在之前学习c语言的时候,对于一些字符串,会初始化字符数组表... 目录一、什么是String二、如何定义一个String1. 用双引号定义2. 通过构造函数定义三、St
阅读更多...
如何解决mmcv无法安装或安装之后报错问题

如何解决mmcv无法安装或安装之后报错问题

《如何解决mmcv无法安装或安装之后报错问题》：本文主要介绍如何解决mmcv无法安装或安装之后报错问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录mmcv无法安装或安装之后报错问题1.当我们运行YOwww.chinasem.cnLO时遇到2.找到下图所示这里3.
阅读更多...
浅谈配置MMCV环境,解决报错,版本不匹配问题

浅谈配置MMCV环境,解决报错,版本不匹配问题

《浅谈配置MMCV环境,解决报错,版本不匹配问题》：本文主要介绍浅谈配置MMCV环境,解决报错,版本不匹配问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录配置MMCV环境,解决报错,版本不匹配错误示例正确示例总结配置MMCV环境,解决报错,版本不匹配在col
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2