粒子滤波器/卡尔曼滤波局限/状态空间模型/蒙特卡罗方法/重要性采样/重要密度函数/重采样/粒子退化 的核心思想+ Matlab代码

--》是递归贝叶斯滤波的一种实现

--》以高计算量为代价换取能表示任何一种分布形式

--》用随机样本表示，用一组加权样本表示后验

--》在局部化的背景下，粒子根据运动模型进行传播，然后根据观察结果的可能性对它们进行加权，在重新采样的步骤中，新粒子的绘制概率与观察到的可能性成正比

--》从存储成本和对不断变化的信号特性的快速适应的角度来看，可以实现数据到达时进行实时处理

--》用于对非线性（ nonlinear ）非高斯（non-Gaussian）模型的估计

粒子滤波器思想：用测量更新权重，根据权重来重采样，用模型来在空间转移粒子。

目标跟踪问题/状态空间模型

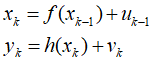
h表示对真实值x的一种有规律的扭曲，所以观测是扭曲过的真实加上噪声。

关于系统模型：为什么只用系统模型不能完全表征目标的方位？--》因为由噪声：在GPS中可以理解为汽车的飘移或者因为违停而被脱走的汽车（绑架机器人）。

说到噪声，这里提一下最小二乘的思想：对于线性模型: y=h*x+v , 很自然的想到，我们要想获得最准确的估计值，我们可以求Σ(y-h*x)^2，当它达到最小时，我们的估计值最接近真实值，这里可以理解为一种对（向量）x的遍历，然后让真实值和我们的观测相匹配。

卡尔曼滤波器的局限

卡尔曼滤波器利用了高斯分布是共轭分布的性质，或者说高斯分布是一个能被参数化的分布，粒子滤波器是对非参数化分布的一种表示形式。当模型和数据是非线性时，用卡尔曼滤波器会得到一些奇怪的非高斯分布。一些算法可以将非线性系统投影成线性系统。

蒙特卡洛方法(Monte Carlo method)：

蒙特卡洛方法是一种对随机变量数字特征的估计方法，可以简单理解为他是在样点和参数之间的一种转换：

从概率分布产生样点《——》从样点建立参数分布

概率质量函数(Probability mass function)：正因为这样才能代表非高斯分布——那些不能用公式准确描述形容的分布，通过散点避免了线性的问题。

重要性采样( Importance Sampling )：

核心思想：形容如何给点赋予权值。

Q是已知的分布，也叫重要性概率密度函数。

权重的积分为1(归一化)，粒子点数越多，对概率的拟合程度越好，当点数无限多时，概率质量分布PMF就是概率分布PDF了。

我们知道粒子滤波器用加权粒子来表示概率分布，那么我们如何获得这些粒子呢？

如果是某分布高斯分布，由于它是参数化的方法，会有其专门的生成算法，比如想生成10个符合标准正态分布N~(0,1)的粒子，可以用matlab函数： 1*randn(1,10);

那其他分布呢？我们这时就用到了importance sampling

通过产生一个已知的参数化分布，然后考虑这个已知的参数分布和未知非参数化分布（目标）的差异——即是权重，具体做法是：

权重w(i)=非参数化分布在某处的值p(i)/参数化已知分布对应的值q(i)

这样用参数化已知分布*权重即是非参数化目标分布对应的概率密度（或者说是分布），所以以这种方法可以生成对应分布的点。

权重相当于对已知概率分布进行变形。

对于目标运动模型，我们可以基于运动和观察，通过预测步骤从这个容易发生样本参数化分布q中抽取样本，我可以很。

通过系统运动模型和观测模型，预测（prediction）通过系统运动模型，从容易建立样点、已知的参数分布产生点；然后用观测方程来作更正（correction）

W（tj）=target（tj）/proposal（tj）,这里tj=ki，k次i个，重采样就是要利用大权重（概率）的点来生成下一次的点，而舍弃那些权重小的点。

简单来说，就是通过已知参数分布（高斯）来生成点，然后根据非参数分布的对应点的PMF和高斯对应位置的PDF之间的差异（权重w）来给生成的这些点来赋值，此时要注意对应关系。

重要密度函数q的选择(Good Choice of Importance Density)

重要密度函数的作用：概率转移、后验搬移，可以理解为一种对概率密度（点的权重）刷新的方法。

选择重要性概率密度函数的一个标准是使得粒子权值{w(k)(i)}(i=1:N)的方差最小，这表示的是“不确定中的确定性”的含义。

通常可以选择状态变量的转移概率密度函数p(x(k) | x(k-1))作为重要性概率密度函数q，此时粒子的权值是：

w(k)(i) = w(k-1)(i) * p(y(k) | x(k)(i))

这个式子中的w是权值，p可以理解为贝叶斯公式中的似然函数，这里是用围绕观测y产生的“似然函数”将对应粒子的权值进行刷新。

因此通过q围绕着观测y生成的，而w衡量了q与通过系统运动模型生成的p的关系，可以近似理解为他俩越接近的点的权值越大.

重采样方法(Resampling)

核心思想：让我们的概率密度分布更加紧凑地分布于可能性更大地点上.

需要重采样是因为本质上是因为我们的点数是有限的（由于计算机的计算能力有限，我们只能表示有限个点），当有些粒子去了概率为0（权值低）的区域时，我们就认为它们不好（Bad），所以我们应该将Bad点舍弃，而保留那些在概率高的（权值高的）区域的点，并且新生成的点被赋予相同权值，然后开始下一次递归。这就是所谓的适者生存——“survival of the fittest principle”.

如果点数无穷、计算能力无穷的话就不存在resample，因为假设只有1%的点是有效点的话，有效点的数量为（0.01*∞）=∞，依旧能保持点数的丰富性，而点数有限。而如果计算能力有限、点数有限还不重采样的话，那么就无法长时间分析系统（跟踪目标），因为这种情况下粒子滤波器会发散，发散的原因是误差积累，每一次进行计算生成点时都会产生误差，这些误差会积累并且不可逆（无法恢复），除非有无限个点。

举个例子：考虑函数y=x^100，若x是连续的话，则点数也连续，即不存在误差（可以认为连续情况属于一种遍历，把有噪声作用的情况也遍历了），而若x是离散的话，本来x=2处的点对应y=2^100，这时有了0.1的误差，y=（2.1)^100，这种误差是非常大的，而且你下一次计算时还会有新误差，这两次误差一积累，就会造成更大的误差。

粒子退化（sample impoverishment）

粒子退化与权值退化的区别：权值退化是说计算量的问题，减少无效计算，而粒子退化是形容多样性。

粒子滤波器Matlab仿真效果和代码

%% 
clear all
close all
clc

%% 初始化变量
set(0,'DefaultFigureWindowStyle','docked') 
x = 0.1;
x_N = 1; 
x_R = 1; 
T = 75; 
N = 100;

V = 2; 
x_P = [];

for i = 1:N%围绕x=0.1生成先验粒子
    x_P(i) = x + sqrt(V) * randn;
end

figure(1)
clf
subplot(121)
plot(1,x_P,'.k','markersize',5)
xlabel('time step')
ylabel('flight position')
subplot(122)
hist(x_P,100)
xlabel('flight position')
ylabel('count')
pause

z_out = [x^2 / 20 + sqrt(x_R) * randn];  
x_out = [x];  
x_est = [x]; 
x_est_out = [x_est]; 
%把均值当作估计值

for t = 1:T
    
    x = 0.5*x + 25*x/(1 + x^2) + 8*cos(1.2*(t-1)) +  sqrt(x_N)*randn;%真实非线性运动方程
    z = x^2/20 + sqrt(x_R)*randn;%我们通过观测方程观测
    %Here, we do the particle filter，生成点
    for i = 1:N
        % 根据上一次的N个粒子（prior）x_P，和非线性控制，生成下一次的粒子
        x_P_update(i) = 0.5*x_P(i) + 25*x_P(i)/(1 + x_P(i)^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
        %根据x_P_update和观测方程生成对应观测z_update
        z_update(i) = x_P_update(i)^2/20;
        %虽然观测到了z，但是不能认为z就是真实值，用观测真值z计算每个z_update中粒子的权重，权值赋予依据是似然函数q，算是一种对产生点的考核
        P_w(i) = (1/sqrt(2*pi*x_R)) * exp(-(z - z_update(i))^2/(2*x_R));
    end
    
    P_w = P_w./sum(P_w);
    
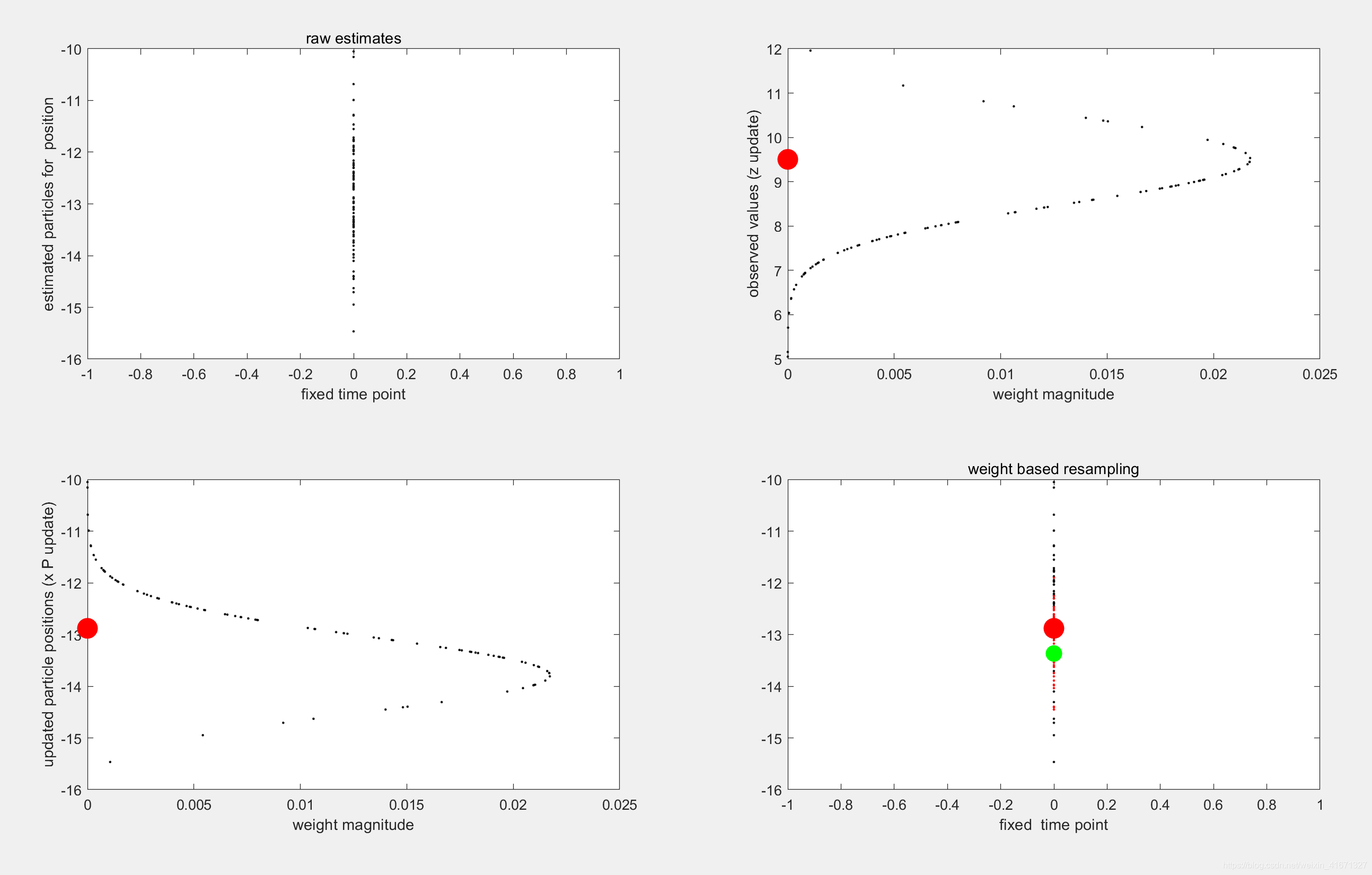
    %画出由上一次的粒子生成的点和由观测方程生成的每个点的观测
    figure(1)
    clf
    subplot(221)
    plot(0,x_P_update,'.k','markersize',5)
    title('raw estimates')
    xlabel('fixed time point')
    ylabel('estimated particles for  position')
    subplot(222)%对应粒子的权重
    plot(P_w,z_update,'.k','markersize',5)
    hold on
    plot(0,z,'.r','markersize',50)
    xlabel('weight magnitude')
    ylabel('observed values (z update)')    
    subplot(223)%粒子的权重
    plot(P_w,x_P_update,'.k','markersize',5)
    hold on
    plot(0,x,'.r','markersize',50)
    xlabel('weight magnitude')
    ylabel('updated particle positions (x P update)')
    
    %% 重采样
    
    for i = 1 : N
        x_P(i) = x_P_update(find(rand <= cumsum(P_w),1))%这是一种方法：计算累加权重值，令其大于随机数，在平均意义上剔除小的权值所所对应的x_P_update
        
    end
    
    x_est = mean(x_P);%对重采样后的点均值作为估计
     
    subplot(224)%
    plot(0,x_P_update,'.k','markersize',5)%重采样前的点用黑色小点画出
    hold on
    plot(0,x_P,'.r','markersize',5)%重采样后的点用红色小点点画出
    plot(0,x,'.r','markersize',50)%仿真的真实值值用绿色大点画出
    plot(0,x_est,'.g','markersize',40)%我们的估计值用绿色大点画出
    xlabel('fixed  time point')
    title('weight based resampling')

    x_out = [x_out x];
    z_out = [z_out z];
    x_est_out = [x_est_out x_est];
    drawnow;
end

t = 0:T;
figure(1);
clf
plot(t, x_out, '.-b', t, x_est_out, '-.r','linewidth',3);%真实轨迹和我们的估计轨迹
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('  position');
legend('True  position', 'Particle filter estimate');