课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记

本文主要是介绍课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、 引言

   该论文针对三轴加速度计、磁通门和速率陀螺随钻测量系统，建立了基于四元数井眼轨迹参数测量模型，并依据状态方程和量测方程，应用2个扩卡尔曼滤波器、1个无迹卡尔曼滤波器和磁干扰校正系统对加速度计、磁通门信号进行滤波、校正，形成了基于数据融合的近钻头井眼轨迹参数动态测量方法。
   基于数据融合算法的近钻头井眼轨迹参数动态测量方法的测量流程如下图所示：

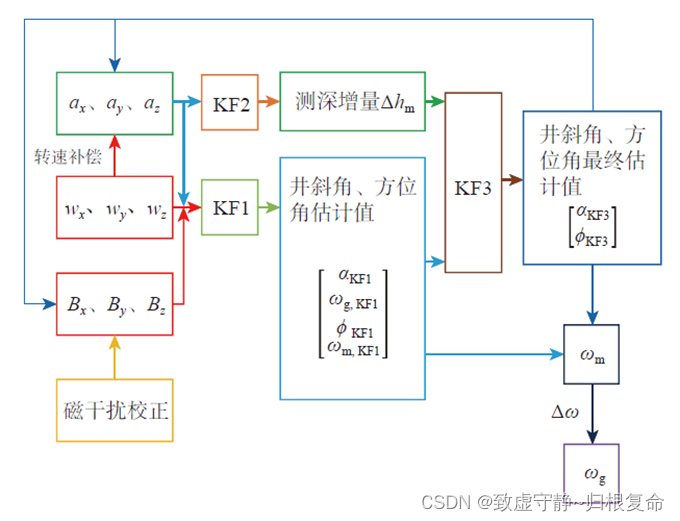
   测量步骤：
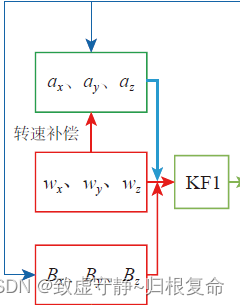
   1. 将加速度计、磁通门、转动角速度四元数带入KF1滤波器，进行扩展卡尔曼滤波，得出井斜角、方位角估计值：

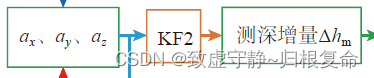
   2. 将加速度计四元数带入KF2 滤波器，进行扩展卡尔曼滤波，得出测深增量$\Delta h_m$

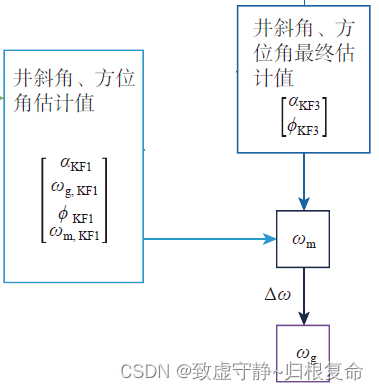
   3. 将测深增量$\Delta h_m$、井斜角、方位角估计值带入KF3 滤波器，进行无迹卡尔曼滤波，得出井斜角、方位角最终估计值:

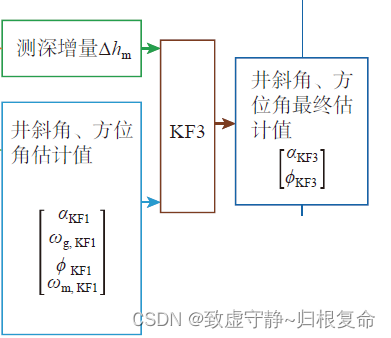
   4.利用井斜角、方位角最终估计值计算磁性工具面角${\omega }_m$与重力工具面角的差$\Delta \omega$

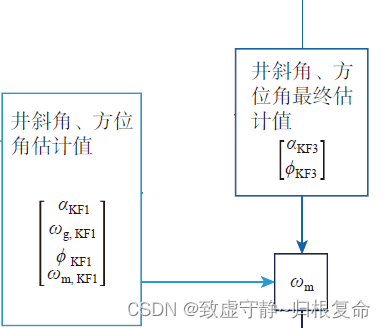
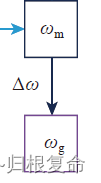
   5.利用磁性工具面角和角差$\Delta \omega$求出重力工具面角${\omega }_g$

   后面的部分会对上述五个步骤进行详细的介绍，下面将进行近钻头动态井眼轨迹测量模型的探讨。

1.1 近钻头动态井眼轨迹测量模型

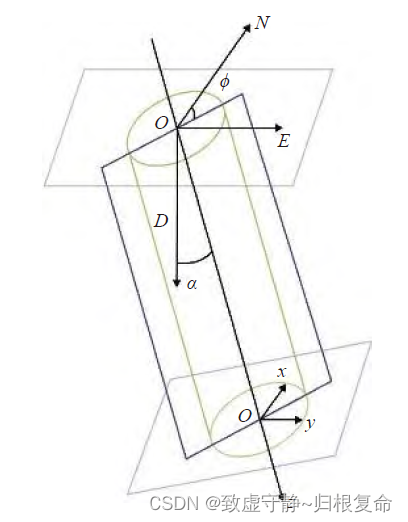
   近钻头动态测量系统由三轴加速度计、三轴磁通门和角速率陀螺仪组成，根据地理坐标系$O-NED$ 和钻具坐标系$O-xyz$ 的对应关系，建立欧拉角转换矩阵，并转换为四元数,k 时刻姿态转换矩阵T表示为：

   $$T(k)=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& q_0^2-q_1^2+q_2^2-q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_1{q}_0)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]$$
   OK,模型、四元数建立完成，下面仔细品味五个步骤：

二、 数据融合近钻头井眼轨迹参数动态测量方法

2.1 估计近钻头井斜角、方位角的扩展卡尔曼滤波算法KF-1

   基于四元数的KF1 的状态方程和量测方程：
$$Q(k+1)=(I+t_{s}A(k))Q(k)+w(k)$$
$$Z(k+1)=F(Q(k))+v(k)$$
   Q(k) 为k 时刻的状态值；I 为单位矩阵；ts 为采样周期；w(k) 为k 时刻系统高斯白噪声；v(k) 为k 时刻传感器观测噪声；A(k) 为k 时刻状态转移矩阵；F(x) 为非线性函数；Z(k+1) 为k+1 时刻的观测值。
   $$Z(k+1)=\left[\begin{array}{c}{B}_x\\ B_y\\ B_z\\ a_x\\ a_y\\ a_z\end{array}\right]=\left[\begin{array}{c}T(k)\left[\begin{array}{c}Bcos\theta \\ 0\\ Bsin\theta \end{array}\right]\\ T(k)\left[\begin{array}{c}0\\ 0\\ g\end{array}\right]\end{array}\right]+v(k)$$
   $$Q(k+1)=\left(\begin{array}{c}I+t_s\left[\begin{array}{cccc}0& -w_x(k)& -w_y(k)& -w_z(k)\\ w_x(k)& 0& w_z(k)& -w_y(k)\\ w_y(k)& -w_z(k)& 0& w_x(k)\\ w_z(k)& w_y(k)& -w_x(k)& 0\end{array}\right]\end{array}\right)$$
  

三轴加速度信号、三轴磁通门信号、角速率陀螺信号进行数据融合后，采用扩展卡尔曼滤波算法，得到最优姿态估计，动态解算出钻井工具的实时姿态参数，确保钻具姿态测量计算的精度，减少计算量，对四元数Q 进行更新

   上述是论文中的引用，这句话我在思考了好几分钟，精简了一下：三轴加速度信号、三轴磁通门信号、角速率陀螺信号进行数据融合后，采用扩展卡尔曼滤波算法，得到最优姿态估计；并使用上式，通过陀螺仪测得的三轴角速度对四元数Q 进行更新,计算经过KF1滤波后的下面各值：$$井斜角{\alpha }_{KF1}=arctan\frac{2(q_0{q}_1+q_2{q}_3)}{1-2(q_1^2+q_2^2)}$$
$$方位角{\varphi }_{KF1}=arctan\frac{2(q_0{q}_3+q_1{q}_2)}{1-2(q_0^2+q_3^2)}$$
$$高边工具面角{\omega }_{g,KF1}=arctan\frac{(q_0{q}_2+q_1{q}_3)}{(q_0{q}_1-q_2{q}_3)}$$
$$磁性工具面角{\omega }_{m,KF1}=arctan\frac{(q_0{q}_2+q_0{q}_3)cos\theta +(q_1{q}_2+q_0{q}_3)sin\theta }{(q_0^2-q_1^2-q_2^2+q_3^2)cos\theta +(q_1{q}_3-q_0{q}_2)sin\theta }$$

2.2 估计近钻头测深增量的扩展卡尔曼滤波算法

   根据$a_z=T(k)g+v(k)$，运用扩展卡尔曼滤波器计算系统经过ts 后测深增量$\Delta h_m$。

z 轴加速度计主要受到重力加速度和振动的干扰，由于采样时间$t_s$为毫秒级，在单位采样周期内，重力加速度和振动的干扰可以视为近似相同，可以忽略振动对加速度计测量结果的影响。

   k 为当前采样点，z 轴加速度增量$\Delta a_z$：$$\Delta a_z=a_z(k+1)-gcos({\alpha }_{KF1}(k))$$$$\Delta a_z=\Delta h_m^{\prime \prime }$$
   为了提高对测深增量的估计，对Δhm 进行二阶泰勒展开：$$\Delta h_m(k+1)=\Delta h_m(k)+\Delta h_m(k{)}^{\prime }{t}_s+0.5\Delta h_m(k{)}^{\prime \prime }{t}_s^2$$
   通过对上式对$t_s$分别求一次导、二次导，可得到下面的矩阵表达式：
   KF2 的状态方程和量测方程为：$$\left[\begin{array}{c}\Delta h_m(k+1)\\ \Delta h_m(k+1{)}^{\prime }\\ \Delta h_m(k+1{)}^{\prime \prime }\end{array}\right]=\left[\begin{array}{ccc}1& t_s& t_s^2\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\Delta h_m(k+1)\\ \Delta h_m(k+1{)}^{\prime }\\ \Delta h_m(k+1{)}^{\prime \prime }\end{array}\right]+w(k)$$
$$\Delta a_z=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\left[\begin{array}{c}\Delta h_m(k+1)\\ \Delta h_m(k+1{)}^{\prime }\\ \Delta h_m(k+1{)}^{\prime \prime }\end{array}\right]+v(k)$$

2.3 估计近钻头井眼轨迹参数的无迹卡尔曼滤波算法

   如下图所示，在单位采样时间内，井眼轨迹趋于平滑曲线，可以根据前面2 个测点的狗腿度和KF2输出测深增量对井眼轨迹进行递归式预测：

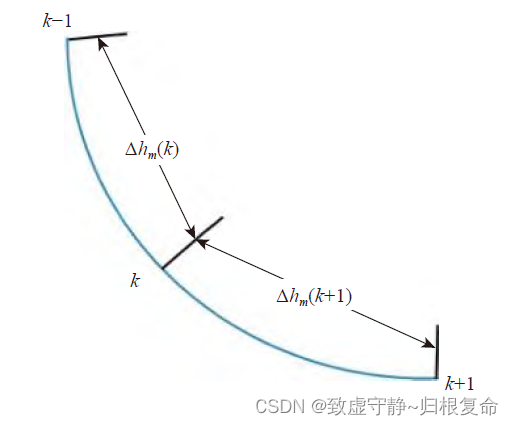
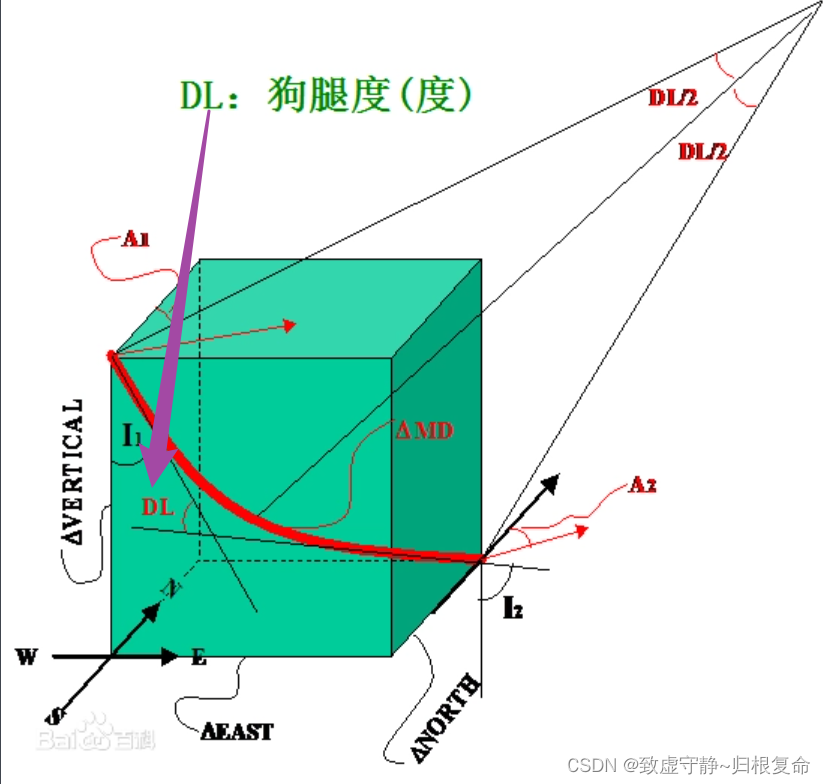
   补充一点关于狗腿度的定义（文字、图片均来源于百度百科！！！）：

狗腿度：从井眼内的一点到另一个点，井眼前进方向变化的角度。该角度既反映了井斜角度的变化，又反映了方位角度的变化，通常又叫全角变化率或井眼曲率。

   下面又是一堆公式袭来，狗腿度的公式是真看不明白，直接截图了：

   KF3 滤波后的井斜角和方位角：$${\alpha }_{KF3}=\alpha (k+1)+v_{\alpha }(k)$$
$${\varphi }_{KF3}=\varphi (k+1)+v_{\varphi }(k)$$
   $v_{\alpha }、v_{\varphi }$分别为井斜角和方位角的系统观测噪声。

2.4 近钻头重力工具面角的估计

   根据旋转测量原理(这个我没找到相关定义，在本篇论文的参考文献12~13中应该有介绍)：同一时刻的重力工具面角与磁工具面角的差与测量时刻的井斜角、方位角、地磁倾角呈现一定函数关系。根据KF3 求出的井眼井斜角和方位角计算磁性工具面角与重力工具面角的差Δω：$$\Delta \omega =-90+arctan\frac{sin{\varphi }_{KF3}}{cos{\alpha }_{KF3}cos{\varphi }_{KF3}-tan\theta sin{\alpha }_{KF3}}$$
   根据Δω，计算旋近钻头动态重力工具面角估计值${\omega }_{dg,e}$：$${\omega }_{dg,e}={\omega }_{m,KF3}+\Delta \omega$$
   我觉得在此处，${\omega }_{m,KF3}$应该是${\omega }_{m,KF1}$，当然，从算法的框架图看出也没啥问题，但是${\omega }_{m,KF1}$是在KF1中给出明确的公式的。

2.5 磁干扰情况下的磁性工具面角

   该部分主要降低磁干扰。磁场的干扰导致磁通门测量的磁场强度发生偏移和变形。磁干扰下的测量结果如下图 所示：

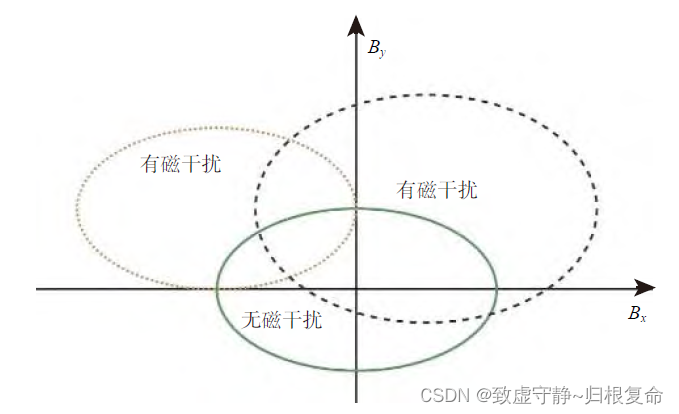
   在实际钻井过程中，井下仪器旋转一圈时，钻深可以忽略不计，可以看作仪器在原地旋转了一圈。z 轴磁通门的测量结果可以认为没有发生变化，而x 轴和y 轴磁通门的测量值不断发生变化，如上图所示。三轴磁通门传感器的测量数据记为（Bx，By，Bx），地球磁场可以看成一个固定值，即：$$B_x^2+B_y^2+B_z^2=C^2$$
   C 为常数.
   根据椭圆校正原理， 对短时间内采集的Bx,By 进行磁干扰校正，得出排除磁干扰的Bxm 和Bym：

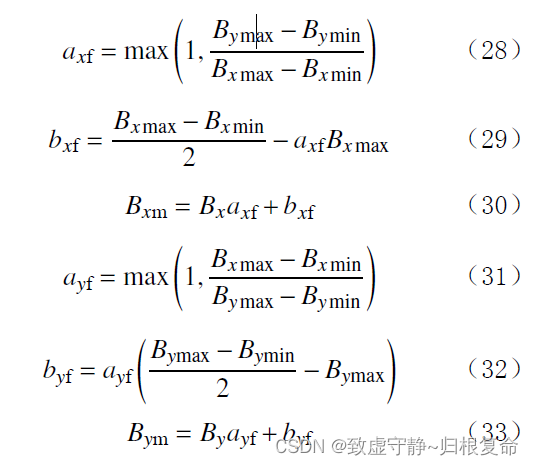
   Bxm 和Bym 为x 轴和y 轴排除磁干扰后的磁场强度。

三、结束

   论文的主要算法部分就是这些，也比较好理解，作者也给出了计算的步骤以及详细的公式，在复现上应该是比较容易的。论文后面部分就是算法效果的验证了，这部分就不再赘述了。

四、往期回顾

课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法（基于磁场的测量系统）
课题学习(三)----倾角和方位角的动态测量方法（基于陀螺仪的测量系统）
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记

这篇关于课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---