完全二叉树、完美二叉树、完满二叉树、计算完全二叉树的结点

完美二叉树、完全二叉树、完满二叉树

一、完美二叉树（Perfect Binary Tree）

对于完美二叉树，我们常用的是另一个名称：满二叉树

完美二叉树的定义：

完美二叉树是一种特殊的完全二叉树，每层都是满的，像一个稳定的三角形

二、完全二叉树**(Complete Binary Tree)**

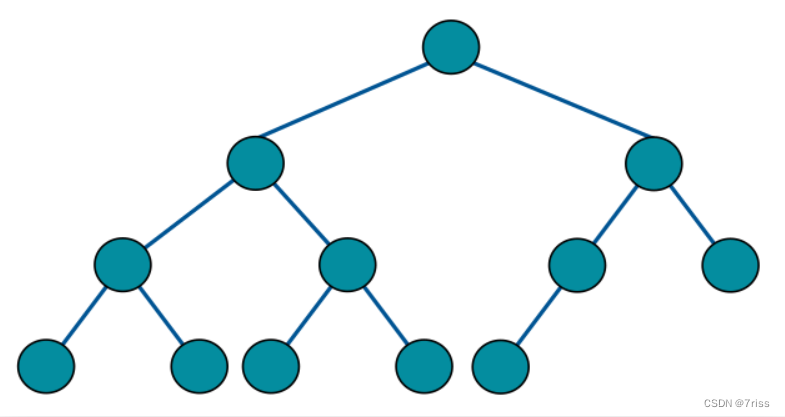
完全二叉树的定义：

全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

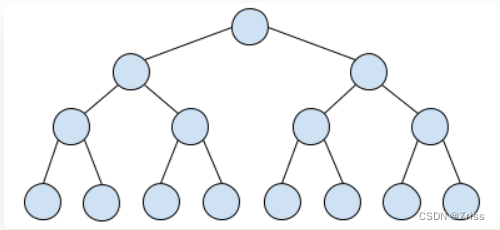
其实理解完全二叉树可以借助于**栈(stack)**的思想。

具体就是我们可以将一棵完美二叉树的所有节点按照编号1…15的顺序依次入栈。然后对栈每一次出栈，栈里保存的结点集构造一棵二叉树都是一棵完全二叉树

完美二叉树和完全二叉树：

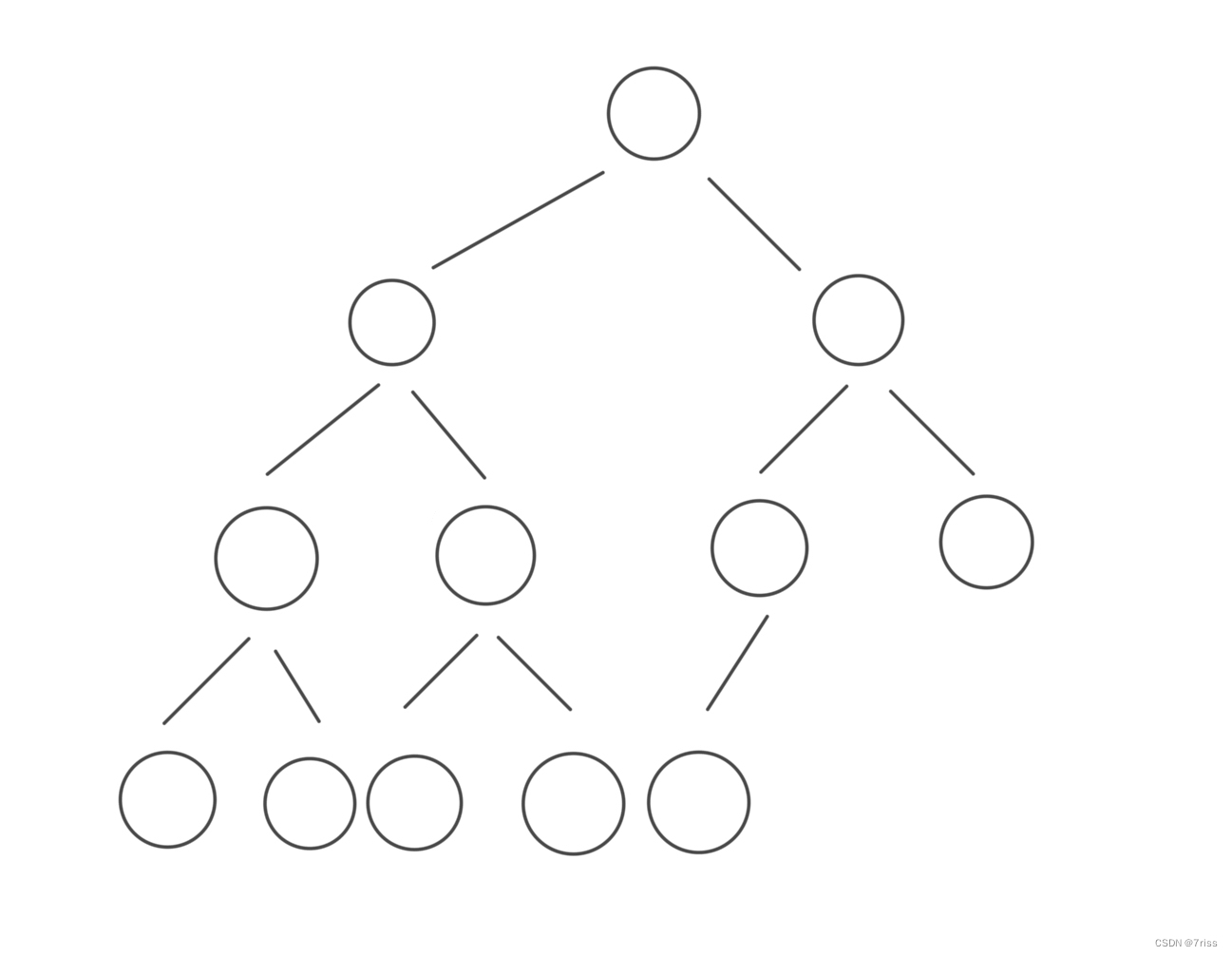
下图是一棵完美二叉树:

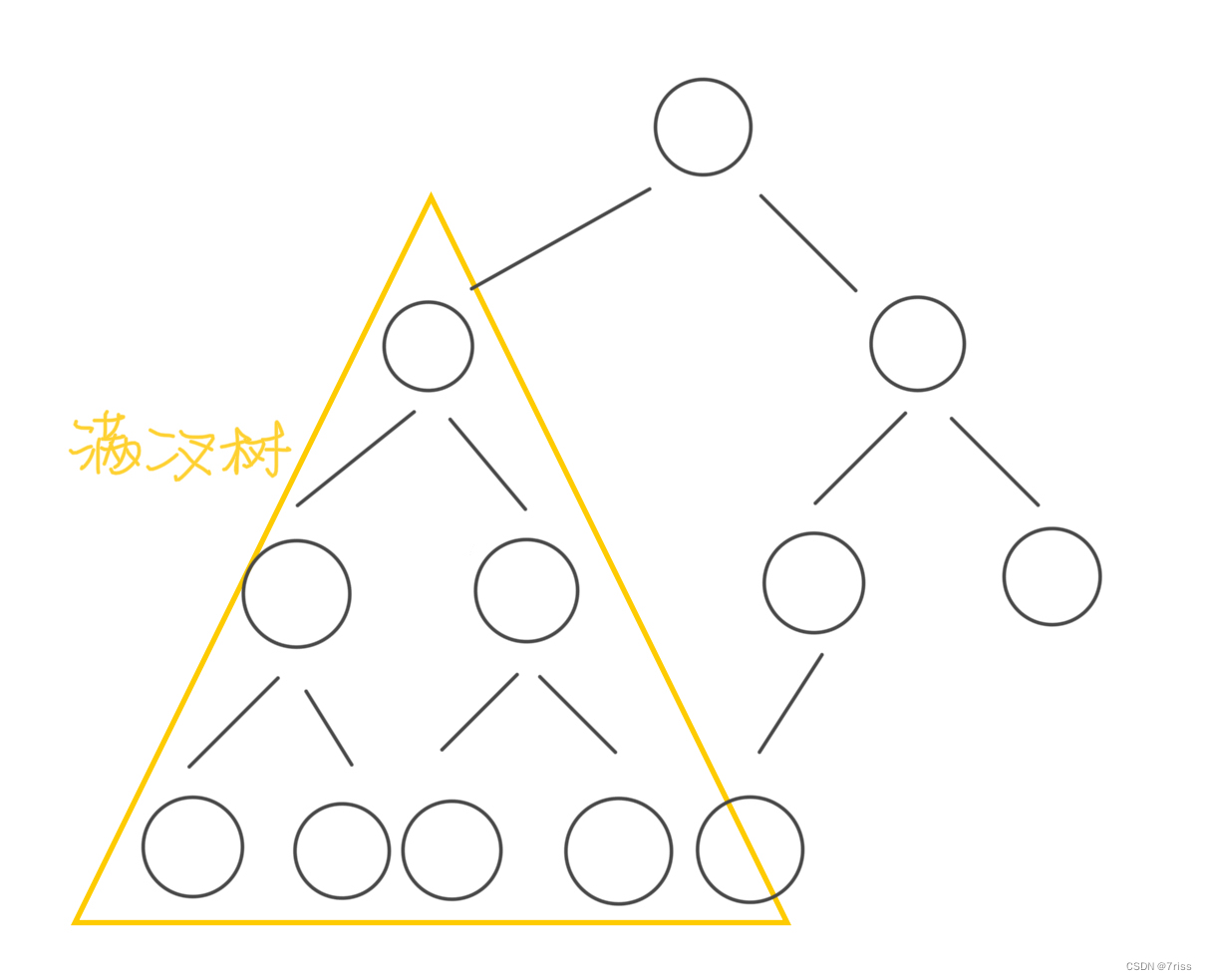
现在将编号为15, 14, …, 9的叶子结点从右到左依次拿掉或者拿掉部分，则是一棵完全(Complete)二叉树

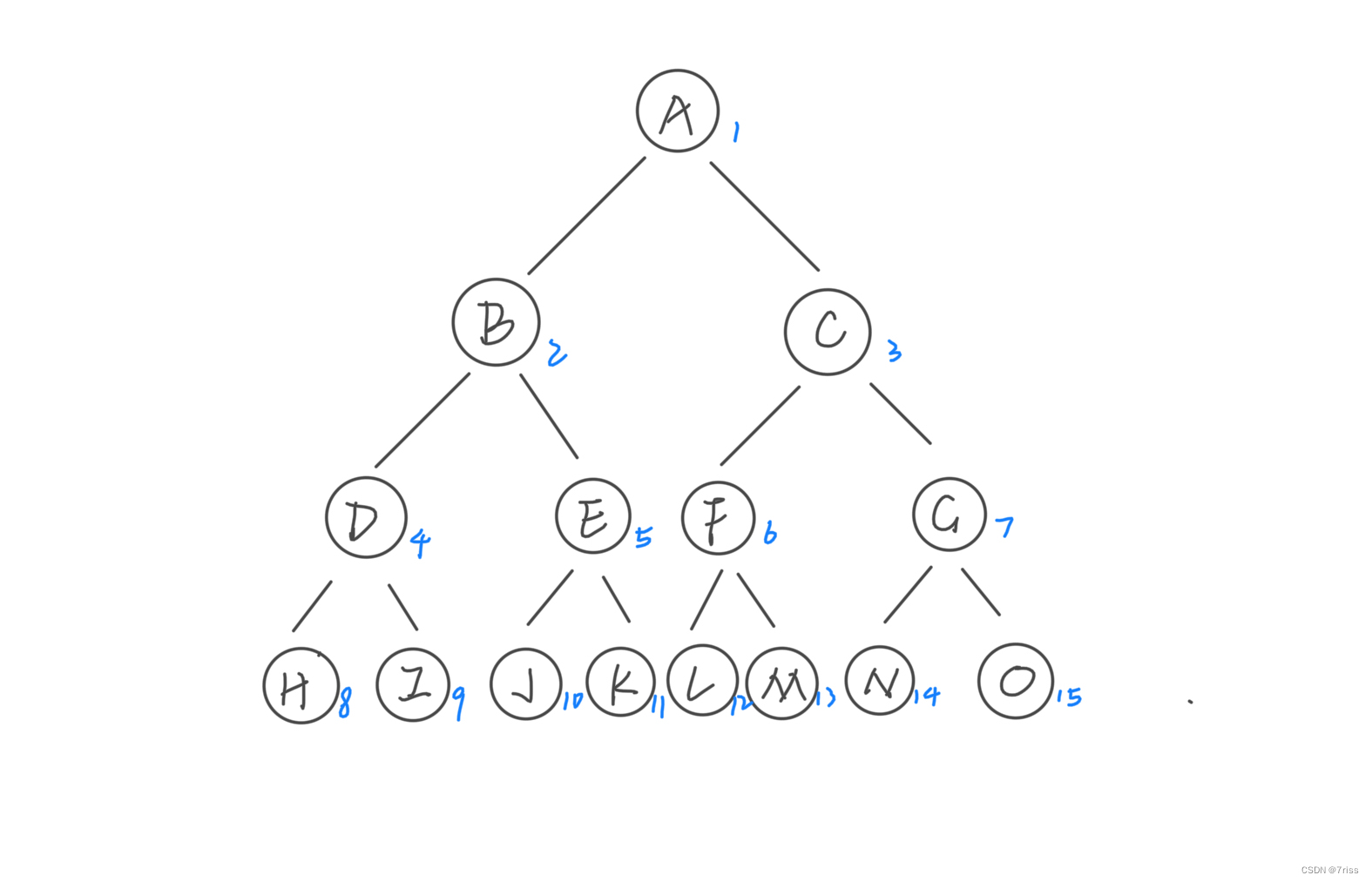
例如将上图中的编号为15, 14, 13, 12, 11叶子结点都拿掉(从右到左的顺序)：

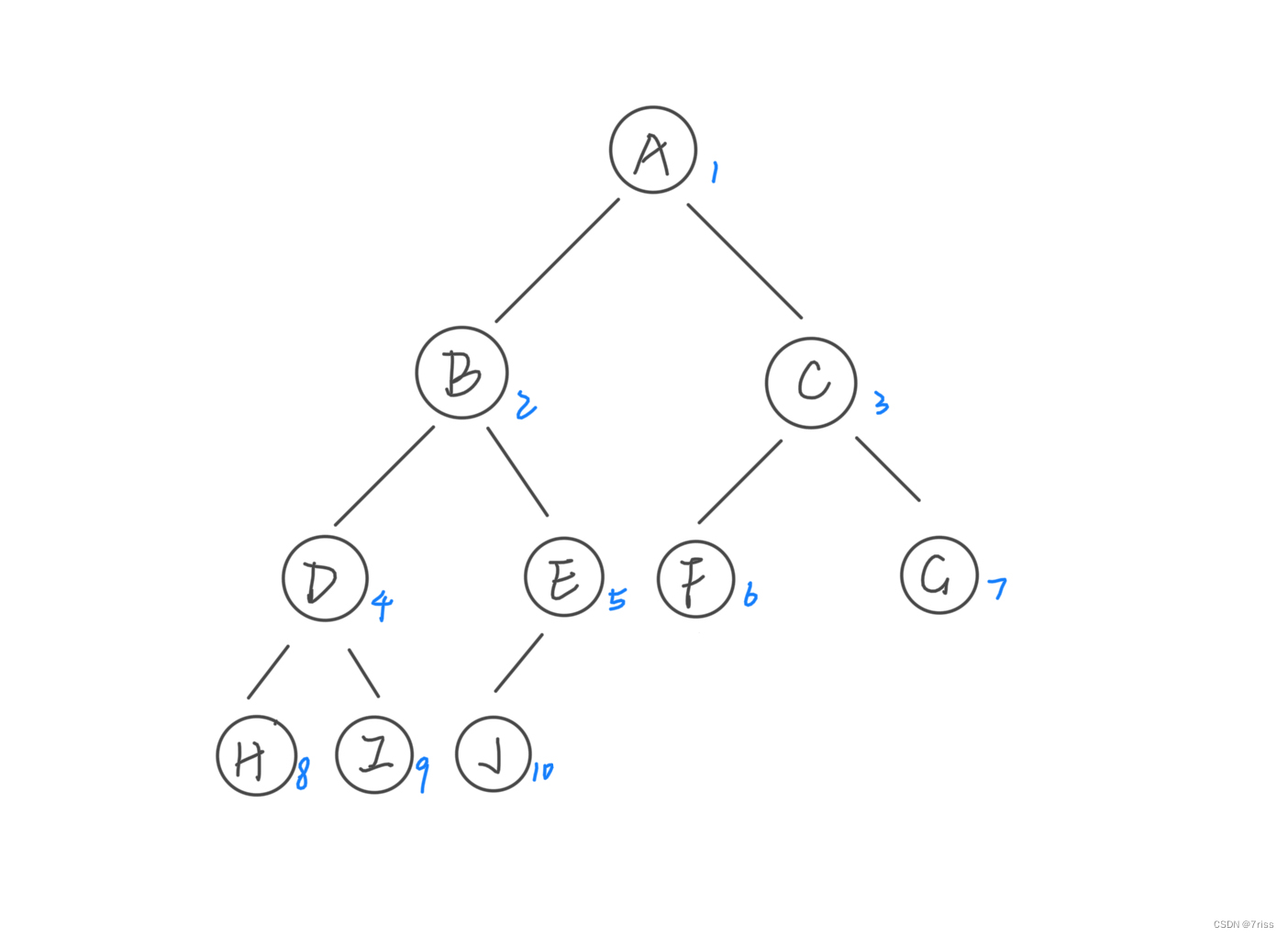
但是如果不是依次拿掉就不满足完全二叉树

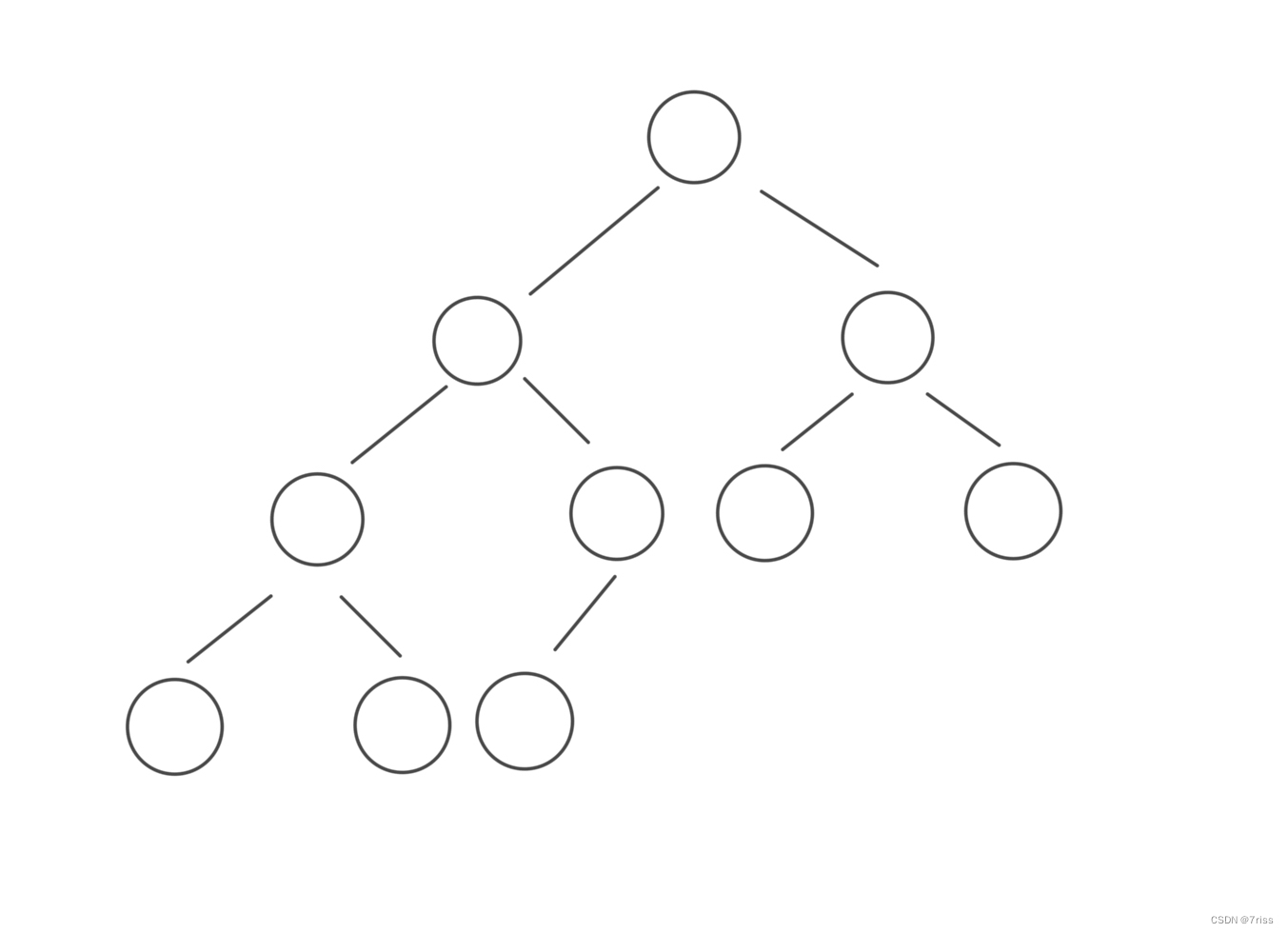
例如将上图编号15，14，13，11叶子结点都拿掉(从右到左的顺序)：

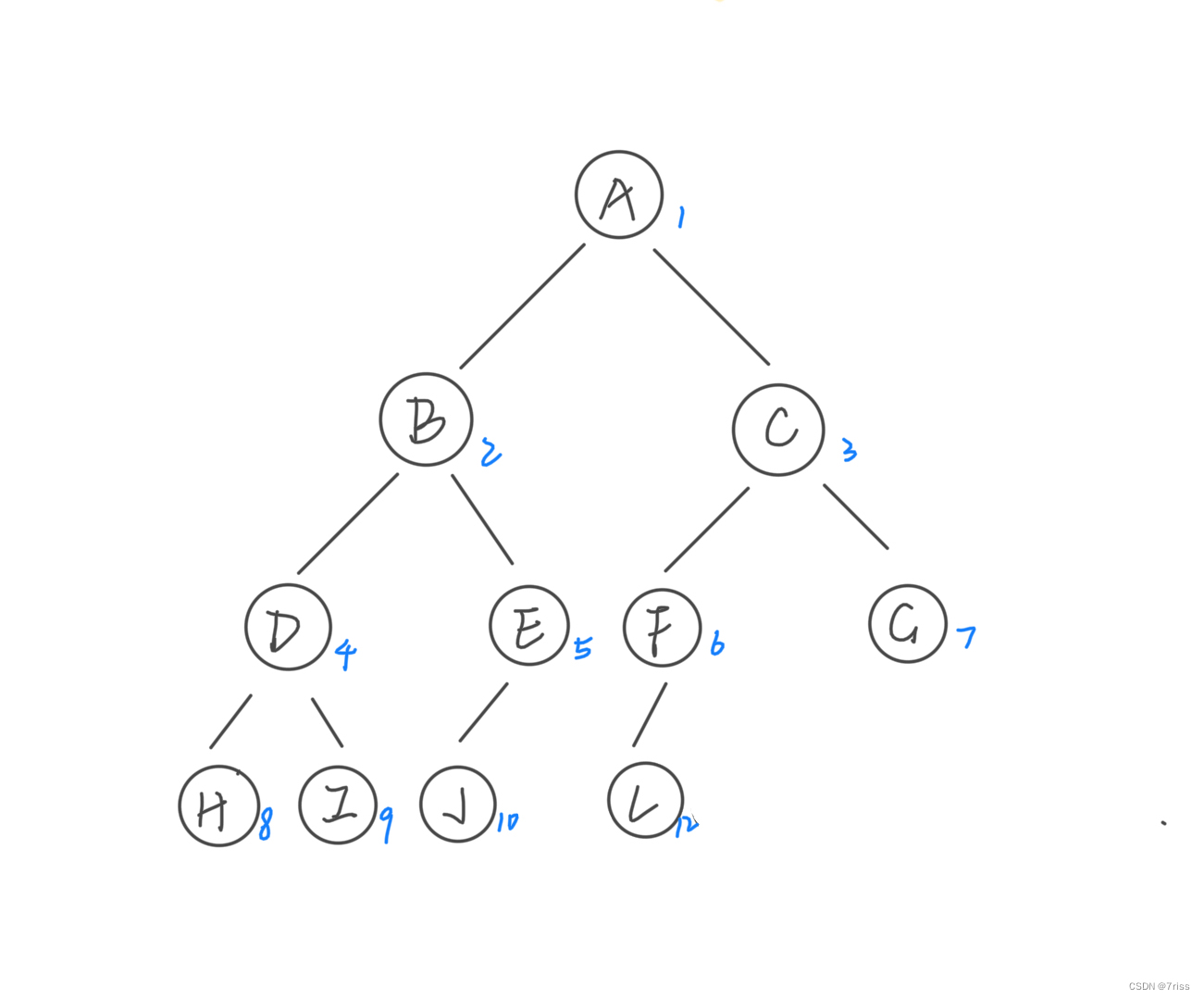
那可以把它变成完全二叉树吗？

要不就是在拿掉编号11的时候也拿掉编号12，要不就是让编号11座位编号5的右孩子，则变成一棵完全二叉树

三、完满二叉树**(Full Binary Tree)**

所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）

四、如何计算完全二叉树的结点数？

222. 完全二叉树的节点个数

public int countNodes(TreeNode root) {if (root == null) return 0;return 1 + countNodes(root.left) + countNodes(root.right);
}

public int countNodes(TreeNode root) {int h = 0;// 计算树的高度while (root != null) {root = root.left;h++;}// 节点总数就是 2^h - 1return (int)Math.pow(2, h) - 1;
}

public int countNodes(TreeNode root) {TreeNode l = root, r = root;// 沿最左侧和最右侧分别计算高度int hl = 0, hr = 0;while (l != null) {l = l.left;hl++;}while (r != null) {r = r.right;hr++;}// 如果左右侧计算的高度相同，则是一棵满二叉树if (hl == hr) {return (int)Math.pow(2, hl) - 1;}// 如果左右侧的高度不同，则按照普通二叉树的逻辑计算return 1 + countNodes(root.left) + countNodes(root.right);
}

复杂度分析：

这个算法的时间复杂度是 O(logN*logN)，这是怎么得到的呢？

直觉感觉好像最坏情况下是 O(N*logN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：

return 1 + countNodes(root.left) + countNodes(root.right);

但是关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发 hl == hr 而立即返回，不会递归下去。

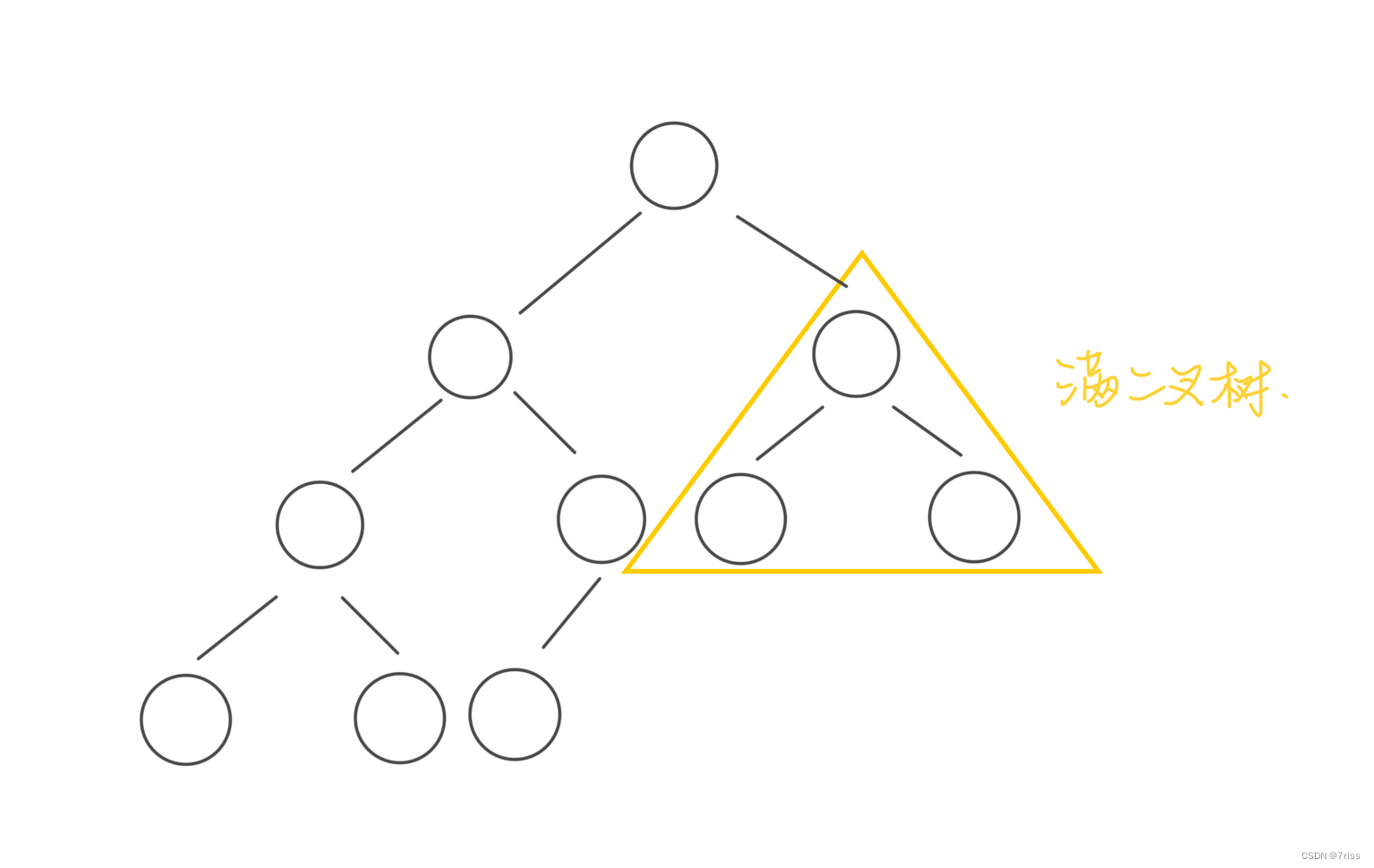
因为一棵完全二叉树的两棵子树，至少有一棵是满二叉树，如图所示：

很明显，由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发 hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。

所以说，「完全二叉树」这个概念还是有它存在的原因的，不仅适用于数组实现二叉堆，而且连计算节点总数这种看起来简单的操作都有高效的算法实现。