试一文讲清“万向节死锁”

目录

引入欧拉角

万向节死锁

从图形上理解万向节死锁

从数学上理解万向节死锁

引入欧拉角

        这里先讲欧拉角。什么是欧拉角？

百度百科：用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角φ组成，为欧拉首先提出而得名。

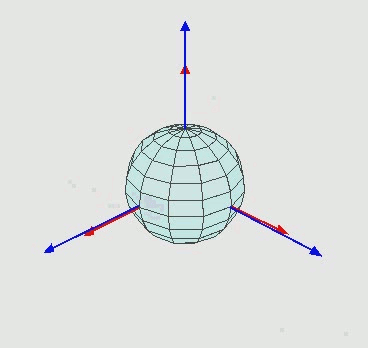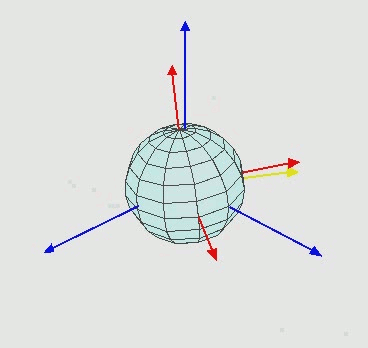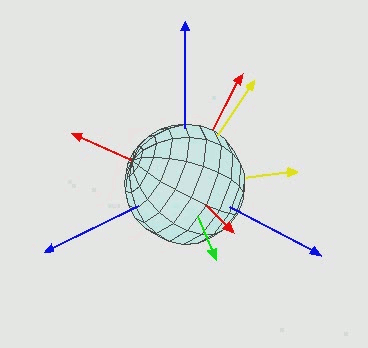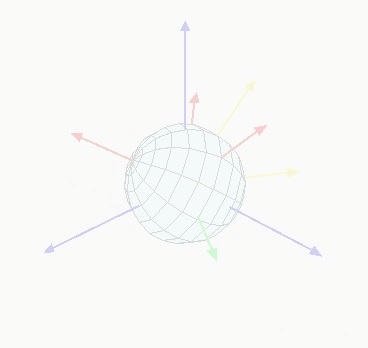
        说的简单些：欧拉角的目的就是描述物体或者物体自身坐标系相对于当前世界的绝对坐标系的一种位姿方向的方法。物体坐标系的变化一般都能分解成三个欧拉角， 也就是三次连续的旋转运动，而且每次旋转的轴线要保证与前后旋转运动的轴线正交。下面的图描述了欧拉角的三次旋转过程：

万向节死锁

        “万向节”一词，我看到的第一印象就是机械设计里的一个典型的传动件，叫做万向连轴器。万向连轴器由两个不共线的轴组成，能多实现转动自由度的传导，如果去查一下这个零件原理动画就能发现与本文所讲的万向节结构有很大相似度。下面开始切入万向节死锁的分析。

        先摆出结论：万向节死锁产生的根本原因，简单说就是欧拉角的3次旋转过程中产生了1次旋转轴的重合，这就导致原来的3个旋转自由度实际退化成为2个有效的自由度，也就是说绕3个轴的旋转等效成了在绝对坐标系中2个轴的旋转。随着我们一步步的分析再回头看该结论对这句话的理解会更加透彻。

从图形上理解万向节死锁

        这里我们把问题尽量简单化，先不必须计较旋转方向，即随意方向旋转随意方向，也先不讲内旋、外旋等多余的知识。如下图所示，黑色坐标系为基于右手坐标系建立的最初的坐标系。

        第一次旋转：绕坐标系x-y-z的x轴旋转θx角度，形成新的坐标系x'-y'-z'；

        第二次旋转：绕坐标系x'-y'-z'的y'轴旋转θy角度，形成新的坐标系x''-y''-z''；

        第三次旋转：绕坐标系x''-y''-z''的z''轴旋转θz角度，形成新的坐标系x'''-y'''-z'''；

        但是，当绕y'轴的旋转角度θy=90度时，会出现一种特殊的情况，如下图所示：

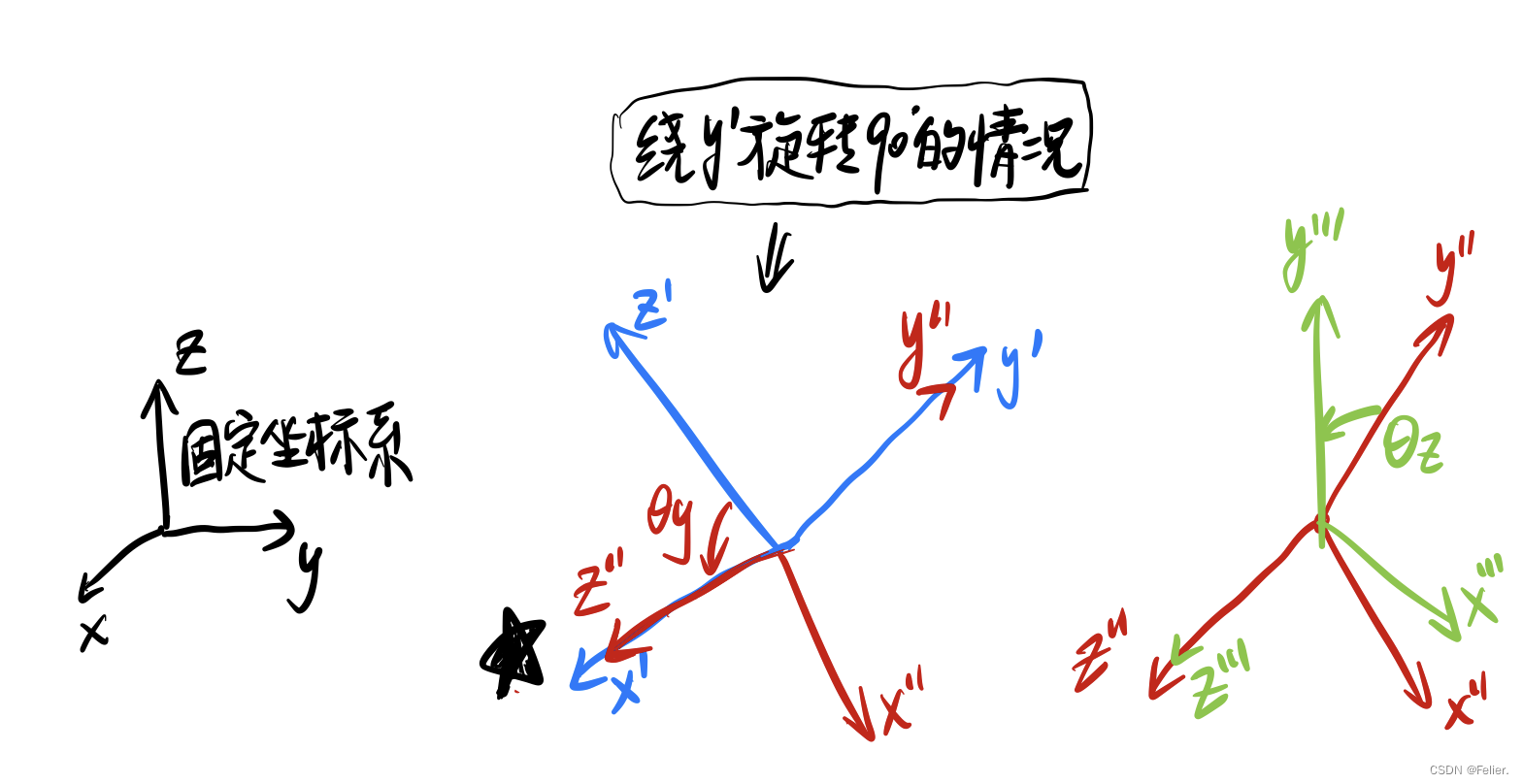
        首先我们假设在我们进行旋转变换的空间内存在某个一成不变的“固定坐标系”，且理解成绝对坐标。默认第一次旋转完全一致，请看第二次旋转过程：如果绕y'轴的旋转角度90度恰好导致旋转后（图中红色）的z''轴与旋转前（图中蓝色）的x'（或者最初的x）轴重合。这样就会导致一个问题出现：就是接下来的第三次旋转因为势必要绕z''轴进行旋转，但是第三次绕z''轴进行的旋转在绝对坐标系下的表现出的效果完全可以靠第一次绕x轴进行的旋转代替。这也就解释为什么在前文讲的“3个旋转自由度实际退化成为2个有效的自由度”，就是因为1、3次的旋转运动相当于重合的。当y'轴的旋转角度-90度时，情况可以类比。

从数学上理解万向节死锁

        数形结合，我们可以从数学上证实上述情况。我直接引用了本科的机器人基础这门课里的几个旋转矩阵，道理相通的，如下图所示是绕不同轴的旋转矩阵。坐标系在空间中的旋转动作，在矩阵计算的表达就是初始坐标系乘旋转矩阵。

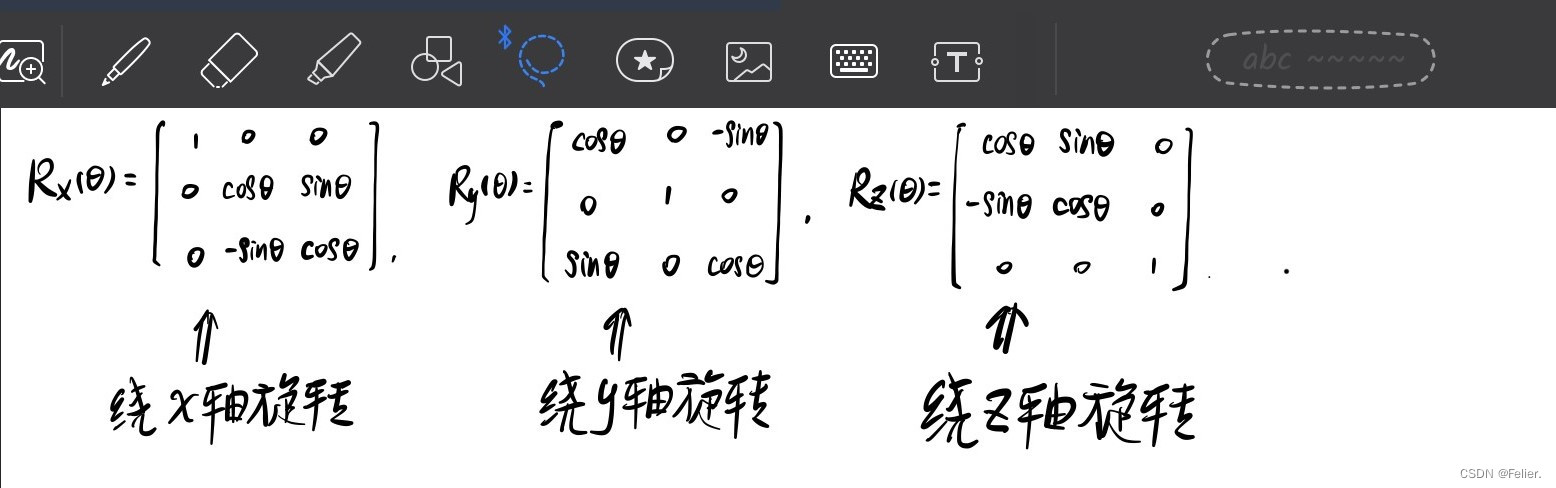
        对于在图形篇里所说的绕y'轴旋转角度为90度的情况下，那旋转矩阵Ry的值自然变成： 

        前文所述的三次旋转变换可以表达为：

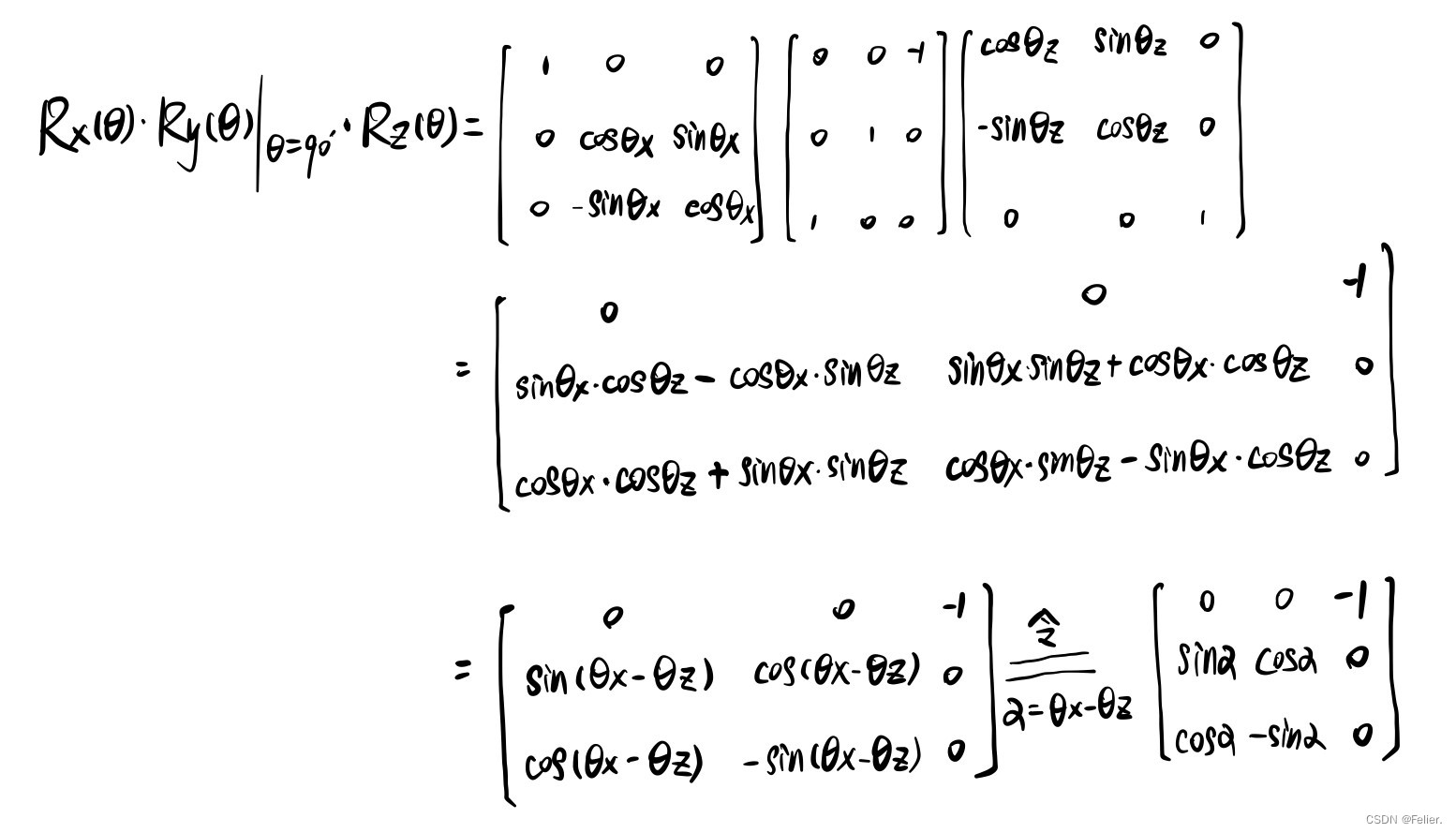
        我们看结果：在锁定y轴旋转自由度的运动为y轴旋转90度的情况下，最终的姿态只是θx-θz的函数。如果令α=θx-θz，就是说本来Rx旋转矩阵中我们把旋转角度在θx的基础上再减少θz，那么根本不需要再乘旋转矩阵Rz，Rx*Ry就OK了，导致的结果就是少了一个自由度的运动，形成了“万向节死锁”。