ZSTU3192 仲夏之夜 (Summer) -- 最小生成树问题解析

放在前面

        还是那句话，因为找不到此题相关的题解，所以凉皮写了这篇文章。作为OI初学者，这道题卡了凉皮很久，现在凉皮AC了这道题，所以兴奋的地和大家分享这篇文章。本文如果有些术语使用不当或者其他错误欢迎在评论区回复。

题目描述

        “一闪一闪亮晶晶，满天都是小星星”，夏天的夜晚，满天繁星。Pty和xx躺在软绵绵的草坪上，仰望这美丽的星空，让人引起无限的遐想！（富有意境的废话）

        Pty开始展开他的想象力：在这片绚丽的星空图上，有n颗星星，从1到n进行编号。现在有n-1条双向星际航道把这n颗星星给连接了起来。每条星际航道都有一个为过路费（正整数），设这n-1条航道的过路费之和是V。Pty给每两个星星之间都连一条星际航道，并且赋予了它们相应的过路费，要求在连完之后：

        对于任意一种能把n颗星星连接起来的m条航道（这m条航道与原始航道不完全相同），满足这m条航道的过路费之和>V。

        请你告诉Pty：能满足他条件的方案里：图中所有的星际航道过路费之和最小是多少？

        Pty将告诉你：这n-1条航道所连接的点，和每条航道的过路费。

题目解释

        1. 原图具有 n 个节点，n-1 条边，显然是一棵树。

        2. 连结所有的节点使得 n 个节点，两两互相连通，应当共有 (n-1)n/2 条边。

        对于任意一种能把 n 颗星星连接起来的 m 条航道（这 m 条航道与原始航道不完全相同），满足这m条航道的过路费之和 >V。

        3. 最令人费解的就应该是上面这句话，注意这里 m 是一个变量，要能连通 n 个节点，m 应当属于 [n-1, (n-1)n/2]，显然要使任意条件成立，只有使这个最小费用 >V，m 取 n-1 时存在最小费用。事实上我们使用最小的费用连通整张图的路径就叫做最小生成树，而使用最少边连通整张图的路径就叫做生成树。最小生成树不一定是唯一的，根据题意，任意非最小生成树的生成树费用严格大于最小生成树。题意即 n 个节点的边饱和图存在唯一的最小生成树。

        4. 求该图的所有边的和的最小值。

输入格式

        第一行，一个数 n，表示星星的个数。

        以后 n-1 行，每行三个数 u, v, w，表示原始航道。u, v 被连接的两个星星，w 航道的过路费

输出格式

        一个数，表示所求的所有航道过路费和。

测试样例

        原题的测试样例过于简单，这里改为我自己的测试样例。

输入：

7

1 2 1

2 4 2

4 3 3

2 5 10

5 6 1

5 7 1

输出：

 152 

样例解释：

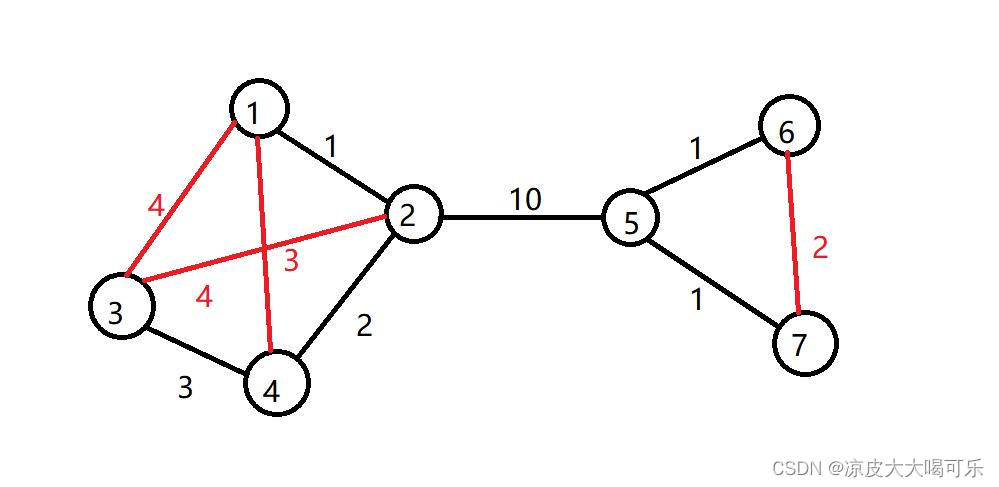
 （因为边比较多，此图删去了一些边没有表现出来，缺失的边全部按边权11表示）

由图我们可以计算出 费用为 18(原始费用) + 2 + 3 + 4 * 2 + 11 * 11 = 152

思路还原

        这道题的新奇之处在于它给定了最小生成树，然后求出图，并且保证这棵树是图的最小生成树，因此我们要保证任意边尽可能的小。

        最小生成树有两个典型算法，Prim 和 Kruskal。我们不妨从这两个典型算法入手。

        我们需要找的是最小边，而与点关联不大，因此可能从 Kruskal 入手比较合适，至少笔者凉皮没有找到基于 Prim 的解法。

        我们不妨假设原始的图是边饱和的，然后使用 Kruskal 算法模拟一遍，好的，那么我们开始。

        找到最小边：1-2 5-6 5-7，我们需要保证这若干条边是全图严格最小的边。
        逐一将三条边列入并查集：1-2 5-6-7
        注意我们将 7 并入 5-6 这个并查集时发现：6-7 之间有一条可以连的边，因为这条边的两个顶点已经被囊括在生成树之中，所以这条边不会出现在之后树生成的考虑范围之中，我们可以确定所连的边的费用的最小值是它所在的集合中最小生成树的边的 最大值+1。
        ...   
        但是在合并两个集合时，我们有多少条可连的边呢？假设合并的两个集合分别有 a 和 b 个元素，那么可连的边应该是 a*b-1。注意这里集合内部的边一定是不可连的，因为我们在之前的操作中已经保证了集合内部的边是饱和的，然后还需要减去一条已有的连接两个集合的边。 

        ...

        例如：我们现在进入了连接最后一条边 2-5 的环节。它将合并两个并查集：2-1-4-3 和 5-6-7，产生 4*3-1 条可连的边，每条边的权为 11。

AC代码 

ahhh~ 终于到了最爱的贴代码环节，这里我就不多废话了（废话真多）。 

// Summer
// Kruskal
// Powered by GreatLiangpi
#include <bits/stdc++.h>
#define int int64_t
#define endl '\n'
#define tomax(x, y) x = max((x), (y))  // Pay attention to the define.
#define pii pair<int, int>
using namespace std;
const int MAX = 100005;struct EDGE {int u;int v;int w;
} edge[MAX];
int father[MAX];  // The father node of the node in the union-find set.
int weight[MAX];  // The weight is the max weight of the edges in the union-find set, not the sum. The attribution is valid for the root of a set only.
int member[MAX];  // The number of the members of the union-find set.bool cmp(EDGE x, EDGE y) {return x.w < y.w;
}int root(int x) {if (father[x] == x) return x;tomax(weight[father[x]], weight[x]);weight[x] = 0;  // remove it is ok.member[father[x]] += member[x];member[x] = 0;return father[x] = root(father[x]);
}void merge(int x, int y) {x = root(x);y = root(y);if (x != y) {tomax(weight[y], weight[x]);weight[x] = 0;  // remove it is ok.member[y] += member[x];member[x] = 0;father[x] = y;}
}int32_t main() {
#ifdef ONLINE_JUDGEcin.tie(0);cout.tie(0);ios::sync_with_stdio(false);
#elsefreopen("in.txt", "r", stdin);
#endifint n;cin >> n;for (int i = 1; i <= n; i++) {father[i] = i;weight[i] = 0;member[i] = 1;}int res = 0;for (int i = 0; i < n-1; i++) {cin >> edge[i].u >> edge[i].v >> edge[i].w;res += edge[i].w;}sort(edge, edge+n-1, cmp);for (int i = 0; i < n-1; i++) {int u = root(edge[i].u);int v = root(edge[i].v);tomax(weight[u], edge[i].w);tomax(weight[v], edge[i].w);int mul = member[u] * member[v] - 1;merge(u, v);res += (weight[v] + 1) * mul;}cout << res;return 0;
}