【续——Python三体问题】

1. 周期稳态三体问题

三体问题（Three-body problem）是天体力学中的基本力学模型。它是指三个质量、初始位置和初始速度都是任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律问题。例如太阳系中，考虑太阳、地球和月球的运动，它们彼此以万有引力相吸引，若假设三个星球都可设为质点，并且忽略其他星球的引力，太阳、地球和月球的运动即可以视为三体问题。

现在已知，三体问题不能使用解析方法精确求解，即无法预测所有三体问题的数学情景，只有几种特殊情况已研究。对三体问题的数值解，会面临混沌系统的初值敏感问题。

2. 作业题目

修改下方示例代码的初始条件和求解器参数，计算一个平面三体运动的周期性稳定解，并作图展示。

参考资料

方法二采用数值解见https://numericaltank.sjtu.edu.cn/three-body/three-body.htm
论文：https://arxiv.org/pdf/1705.00527v2.pdf

3. 方法一（解析法）

小球受到的引力合力等于它所需要的向心力

3.1 原理分析

牛顿平面三体系统的运动由牛顿第二定律和引力定律控制

1. 牛顿第二定律：
   $$F=ma$$
2. 引力定律控制：
   $$F=G\frac{m_1{m}_2}{r^2}$$
   当三个球体相等，并且围成平面等边三角形(边长为 $l$ )的三个顶点，因此一个小球受到另外两个小球的引力，假设小球有一定的初始速度，提出了一种简单的平衡思路，如果小球受到的引力合力等于它所需要的向心力，则三个小球可保持平衡，围着等边三角形的外接圆做匀速圆周运动，永不停息（没有其他干扰）。

a. 初始状态
$$m_1=m_2=m_3=m$$

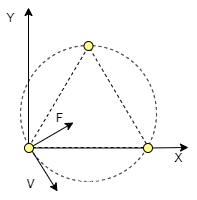
由平衡条件小球受到的引力合力等于它所需要的向心力，合力的加速度恰好等于向心加速度，对小球1分析：
$$G\frac{m}{l^2}\ast \sqrt{3}=\frac{v^2}{r}$$
$r$是小球到圆心的距离($r=\frac{l}{\sqrt{3}}$)
化简：
$$v=\sqrt{G\frac{m}{l}}$$
此公式也是第一宇宙速度（逃离地球）

b. 最终效果

3.2 示例代码

3.2.1 导入numpy、scipy、库

import numpy as np
from scipy import integrate#导入积分求解函数

3.2.2 计算天体的速度和加速度

这里我们考虑天体运行中的三体问题。每一个天体在其他两个天体的万有引力作用下的运动方程都可以表示成3个二阶的ODE。一个天体有三个方向的速度和加速度，因此，一般三体问题的运动方程为18个一阶ODE方程组。'f’函数是随时间t计算合力和距离，并且三个天体的速度和加速度

#计算三个天体的速度和加速度
def f(t, y, args):G, m_A, m_B, m_C = argspos_A, pos_B, pos_C, vel_A, vel_B, vel_C = y[:3], y[3:6], y[6:9], y[9:12], y[12:15], y[15:]r_AB = np.sqrt(np.sum((pos_A-pos_B)**2))r_BC = np.sqrt(np.sum((pos_B-pos_C)**2))r_CA = np.sqrt(np.sum((pos_C-pos_A)**2))F_A = m_A * m_B * G*(pos_B-pos_A)/r_AB**3 + m_C * m_A * G*(pos_C-pos_A)/r_CA**3F_B = m_A * m_B * G*(pos_A-pos_B)/r_AB**3 + m_C * m_B * G*(pos_C-pos_B)/r_BC**3F_C = m_A * m_C * G*(pos_A-pos_C)/r_CA**3 + m_C * m_B * G*(pos_B-pos_C)/r_BC**3return np.hstack((vel_A, vel_B, vel_C, F_A/m_A, F_B/m_B, F_C/m_C))

3.2.3 定义天体的基本参数

#定义天体的初引力常量、质量参数
G = 10.
m_A = 1.
m_B = 1.
m_C = 1.
#此处k为速度的旋转角度（理论上不能取np.pi/6和-5*np.pi/6附近，-np.pi/3是一种平衡位置），v为初始速度大小
k = -np.pi/3
v = np.sqrt(5)
args = (G, m_A, m_B, m_C)
#定义天体的初始速度和位置
pos_A = np.array([0., 0., 0.])
vel_A = np.array([np.cos(k)*v, np.sin(k)*v, 0.])
pos_B = np.array([2., 0., 0.])
vel_B = np.array([np.cos(k+2*np.pi/3)*v, np.sin(k+2*np.pi/3)*v, 0.])
pos_C = np.array([1., np.sqrt(3), 0.])
vel_C = np.array([np.cos(k+4*np.pi/3)*v, np.sin(k+4*np.pi/3)*v, 0.])'''Initial condition y0 must be one-dimensional'''
y0 = np.hstack((pos_A, pos_B, pos_C, vel_A, vel_B, vel_C))t = np.linspace(0, 10, 1000)

3.2.4 选择integrate.ode求解器

我们需要创建一个integrate.ode类的实例，将ODE函数$f$作为参数传给它。

求解器实例保存在变量r中。在使用它之前，需要使用方法set_initial_value设置初始条件。

还可以使用方法set_integrator来选择求解器，可用的求解器名称为：vode、zvode、lsoda、dopri5和dop853。

r = integrate.ode(f)
r.set_integrator('vode', method = 'adams')
r.set_initial_value(y0, t[0])
r.set_f_params(args)

3.2.4 求解ODE

配置完求解器之后，可以调用integrate方法来一步一步求解ODE。不同于使用integrate.odeint函数，我们可以追踪已经积分到哪个点。这种方法提供了更好的灵活性。

dt = t[1] - t[0]
y_t = np.zeros((len(t), len(y0)))idx = 0
while r.successful() and r.t < t[-1]+1e-5:y_t[idx, :] = r.yr.integrate(r.t + dt)idx += 1

3.3 matplotlib画图

3.3.1 导入动画库并定义方程

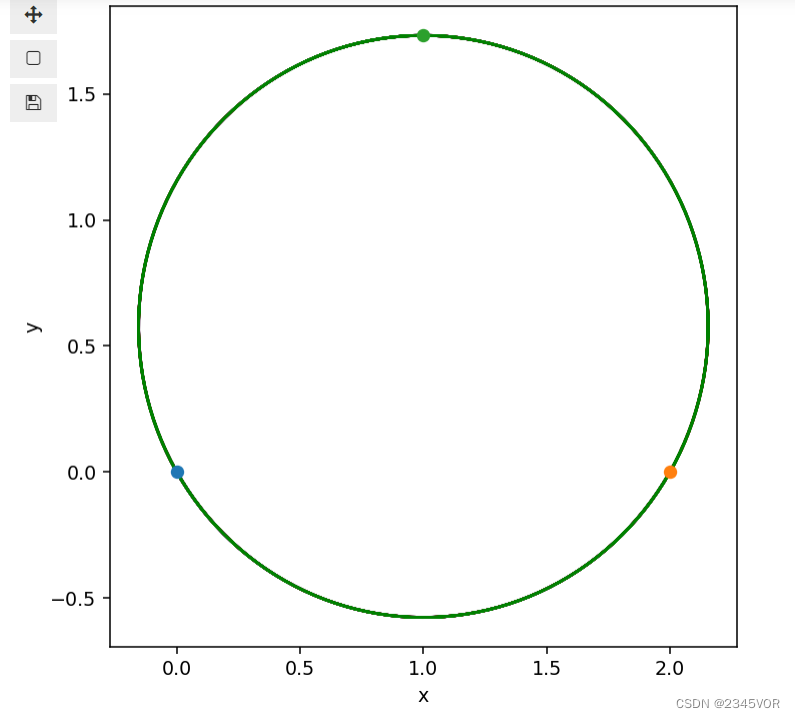
导入matplotlib相关方法，依据前面的数据画轨迹和天体：

%matplotlib widgetimport matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import animationfig, ax = plt.subplots()
ax.plot(y_t[:, 0],y_t[:, 1], lw=1.5, color="blue", label=r"A")
ax.plot(y_t[:, 3],y_t[:, 4], lw=1.5, color="red", label=r"B")
ax.plot(y_t[:, 6],y_t[:, 7], lw=1.5, color="green", label=r"C")
ax.set_xlabel("x")
ax.set_ylabel("y")
point1, = ax.plot(y_t[0, 0], y_t[0, 1], 'o')  
point2, = ax.plot(y_t[0, 3], y_t[0, 4], 'o')  
point3, = ax.plot(y_t[0, 6], y_t[0, 7], 'o')  
#显示所画的图  
plt.show()  

效果

3.3.2 构造动画函数与帧函数：

接着，构造自定义动画函数animate，用来更新每一帧上各个x对应的y坐标值，参数表示第i帧；然后，构造开始帧函数init：

def animate(idx):x1 = np.array(y_t[idx:idx+2, 0])y1 = np.array(y_t[idx:idx+2, 1])x2 = np.array(y_t[idx:idx+2, 3])y2 = np.array(y_t[idx:idx+2, 4])x3 = np.array(y_t[idx:idx+2, 6])y3 = np.array(y_t[idx:idx+2, 7])point1.set_data([x1[0]], [y1[0]])point2.set_data([x2[0]], [y2[0]])point3.set_data([x3[0]], [y3[0]])return point1,point2,point3,
def init():point1.set_data(y_t[0, 0], y_t[0, 1])point2.set_data(y_t[0, 3], y_t[0, 4])point3.set_data(y_t[0, 6], y_t[0, 7])return point1,point2,point3,

3.3.3 参数设置：

接下来，我们调用FuncAnimation函数生成动画。参数说明

1. fig 进行动画绘制的figure
2. func 自定义动画函数，即传入刚定义的函数animate
3. frames 动画长度，一次循环包含的帧数
4. init_func 自定义开始帧，即传入刚定义的函数init
5. interval 更新频率，以ms计
6. lit 选择更新所有点，还是仅更新产生变化的点

fig, ax = plt.subplots()
ax.plot(y_t[:, 0],y_t[:, 1], lw=1.5, color="blue", label=r"A")
ax.plot(y_t[:, 3],y_t[:, 4], lw=1.5, color="red", label=r"B")
ax.plot(y_t[:, 6],y_t[:, 7], lw=1.5, color="green", label=r"C")
ax.set_xlabel("x")
ax.set_ylabel("y")
point1, = ax.plot(y_t[0, 0], y_t[0, 1], 'o')  
point2, = ax.plot(y_t[0, 3], y_t[0, 4], 'o')  
point3, = ax.plot(y_t[0, 6], y_t[0, 7], 'o')  ani = animation.FuncAnimation(fig=fig,func=animate,frames=1000,init_func=init,interval=1,blit=True)
#plt.show()
ani.save('movie.gif', writer='imagemagick', fps=30)

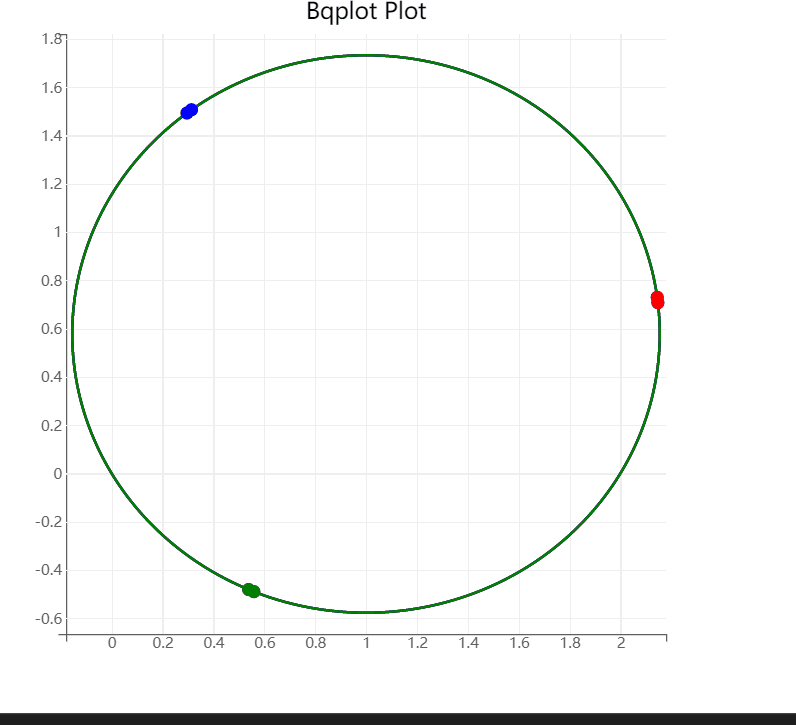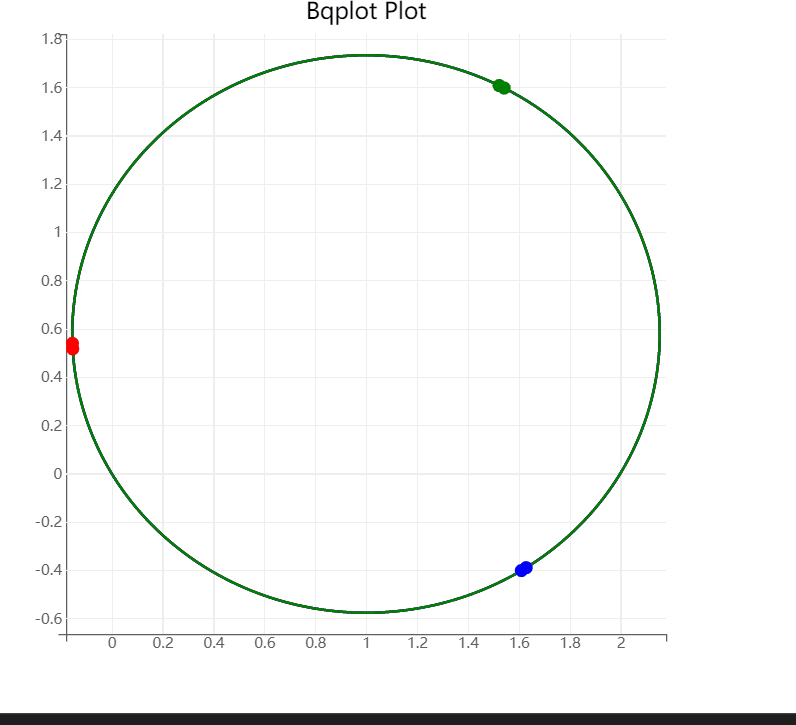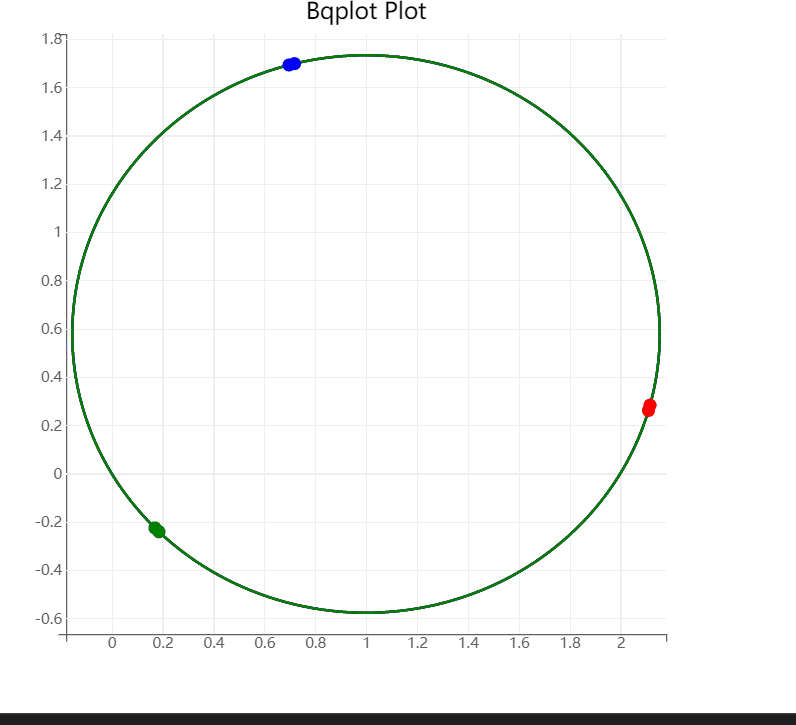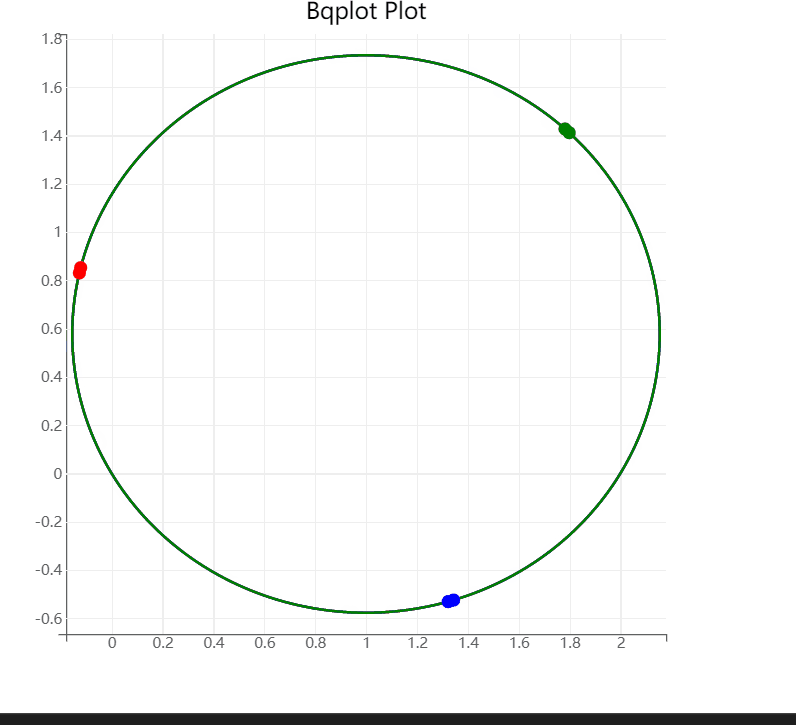
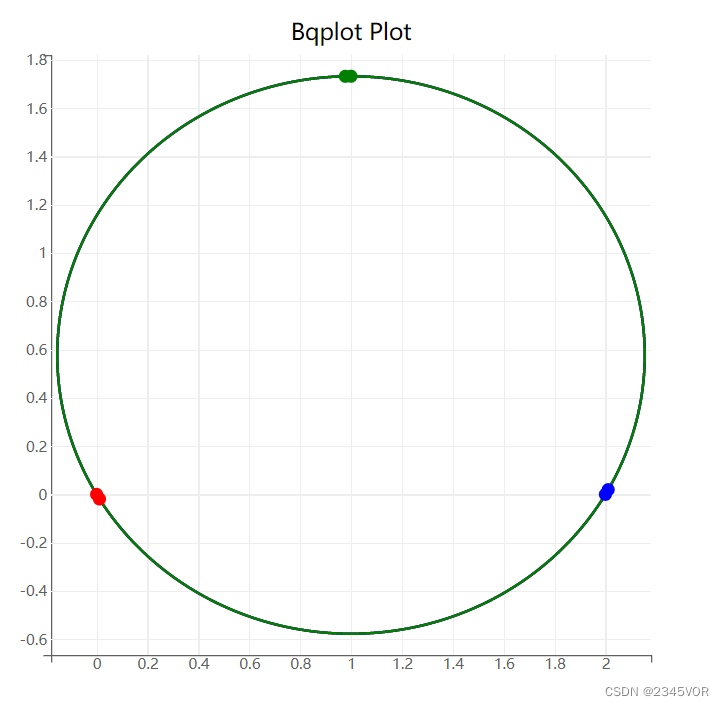
3.4 bqplot画图

计算周期T，画图方式采用bqplot

%matplotlib inline
import bqplot as bq
from bqplot import pyplot as pltfigure = plt.figure(title='Bqplot Plot')
figure.layout.height = '600px'
figure.layout.width = '600px'plot_A = plt.plot(y_t[:, 0],y_t[:, 1], 'r')  # A
plot_B = plt.plot(y_t[:, 3],y_t[:, 4], 'b')  # B
plot_C = plt.plot(y_t[:, 6],y_t[:, 7], 'g')  # C
scatter_A = plt.scatter(y_t[:2, 0],y_t[:2, 1], colors=["red"])
scatter_B = plt.scatter(y_t[:2, 3],y_t[:2, 4], colors=["blue"])
scatter_C = plt.scatter(y_t[:2, 6],y_t[:2, 7], colors=["green"])plt.show()

'''Animation'''
import timeidx = 0
speed = 1#实际周期的speed倍
T1 = time.time()
i = 1
for idx in range(1, len(t)-1, speed):  # Update Chartscatter_A.x = y_t[idx:idx+2, 0]x = np.array(y_t[idx:idx+2, 0])scatter_A.y = y_t[idx:idx+2, 1]y = np.array(y_t[idx:idx+2, 1])if ((abs(x[0])<0.01)& (abs(y[0])<0.01)):T2 = time.time()print(str(i)+'T周期:%s秒'% (T2 - T1))i +=1scatter_B.x = y_t[idx:idx+2, 3]scatter_B.y = y_t[idx:idx+2, 4]scatter_C.x = y_t[idx:idx+2, 6]scatter_C.y = y_t[idx:idx+2, 7]time.sleep(0.01)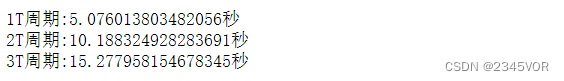

4. 方法2（查表法）

参考论文;https://arxiv.org/pdf/1705.00527v2.pdf

import numpy as np
from scipy import integrate
def f(t, y, args):G, m_A, m_B, m_C = argspos_A, pos_B, pos_C, vel_A, vel_B, vel_C = y[:3], y[3:6], y[6:9], y[9:12], y[12:15], y[15:]r_AB = np.sqrt(np.sum((pos_A-pos_B)**2))r_BC = np.sqrt(np.sum((pos_B-pos_C)**2))r_CA = np.sqrt(np.sum((pos_C-pos_A)**2))F_A = m_A * m_B * G*(pos_B-pos_A)/r_AB**3 + m_C * m_A * G*(pos_C-pos_A)/r_CA**3F_B = m_A * m_B * G*(pos_A-pos_B)/r_AB**3 + m_C * m_B * G*(pos_C-pos_B)/r_BC**3F_C = m_A * m_C * G*(pos_A-pos_C)/r_CA**3 + m_C * m_B * G*(pos_B-pos_C)/r_BC**3return np.hstack((vel_A, vel_B, vel_C, F_A/m_A, F_B/m_B, F_C/m_C))

根据论文选择合适参数，修改天体的基本参数，下面采用I.B-1

G = 1.
m_A = 1.
m_B = 1.
m_C = 1.
x1 = -0.9989071137
x2 = -0.0001484864
v1 =  0.4646402601
v2 =  0.3963456869 
#I.B-1 论文：One hundred and fifty-two new families of Newtonian periodic planar three-body orbits（P8)
args = (G, m_A, m_B, m_C)pos_A = np.array([x1, x2, 0.])
vel_A = np.array([v1, v2, 0.])
pos_B = np.array([-x1, -x2, 0.])
vel_B = np.array([v1, v2, 0.])
pos_C = np.array([0., 0, 0.])
vel_C = np.array([-2*v1, -2*v2, 0.])'''Initial condition y0 must be one-dimensional'''
y0 = np.hstack((pos_A, pos_B, pos_C, vel_A, vel_B, vel_C))t = np.linspace(0, 20, 5000)

r = integrate.ode(f)
r.set_integrator('vode', method = 'adams')
r.set_initial_value(y0, t[0])
r.set_f_params(args)
dt = t[1] - t[0]
y_t = np.zeros((len(t), len(y0)))idx = 0
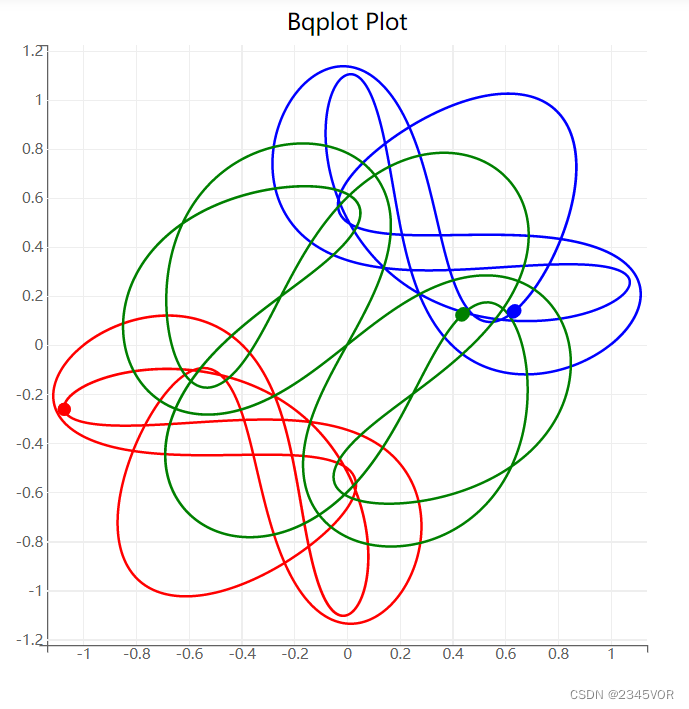
while r.successful() and r.t < t[-1]+1e-5:y_t[idx, :] = r.yr.integrate(r.t + dt)idx += 1import bqplot as bq
from bqplot import pyplot as pltfigure = plt.figure(title='Bqplot Plot')
figure.layout.height = '600px'
figure.layout.width = '600px'plot_A = plt.plot(y_t[:, 0],y_t[:, 1], 'r')  # A
plot_B = plt.plot(y_t[:, 3],y_t[:, 4], 'b')  # B
plot_C = plt.plot(y_t[:, 6],y_t[:, 7], 'g')  # C
scatter_A = plt.scatter(y_t[:2, 0],y_t[:2, 1], colors=["red"])
scatter_B = plt.scatter(y_t[:2, 3],y_t[:2, 4], colors=["blue"])
scatter_C = plt.scatter(y_t[:2, 6],y_t[:2, 7], colors=["green"])plt.show()
'''Animation'''
import timeidx = 0
speed = 2
T1 = time.time()
i = 0
for idx in range(1, len(t)-1, speed):  # Update Chartscatter_A.x = y_t[idx:idx+2, 0]x = np.array(y_t[idx:idx+2, 0])scatter_A.y = y_t[idx:idx+2, 1]y = np.array(y_t[idx:idx+2, 1])if ((abs(x[0]+1)<0.003)& (abs(y[0])<0.003)):T2 = time.time()print(str(i)+'T周期:%s秒'% (T2 - T1))i +=1scatter_B.x = y_t[idx:idx+2, 3]scatter_B.y = y_t[idx:idx+2, 4]scatter_C.x = y_t[idx:idx+2, 6]scatter_C.y = y_t[idx:idx+2, 7]time.sleep(0.01)

参考文献来自桑鸿乾老师的课件：科学计算和人工智能