本文主要是介绍利用离散序列的差分运算寻找序列的下降沿、上升沿、极大值(波峰)、极小值(波谷)的原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们先来看一看对于连续函数,我们通常是怎么求其极值的。
通常我们用函数极值的第一充分条件和第二充分条件来求函数的极值。
函数极值的第一充分条件和第二充分条件的内容如下:
(懒得自己写了,直接把高等数学书上的内容截图发上来吧,大家将就看吧!)


在实际工程中,我们用得最多的是第二充分条件。
说完了连续函数求极值点,自然该说离散序列怎么找极值点了,即我们常说的寻找离散序列的波峰、波谷。
为了说明这个问题,首先我们要知道“离散序列差分运算”的概念。
设有序列 . . . , f ( k − 2 ) , f ( k − 1 ) , f ( k ) , f ( k + 1 ) , f ( k + 2 ) , . . . ...,f(k-2),f(k-1),f(k),f(k+1),f(k+2),... ...,f(k−2),f(k−1),f(k),f(k+1),f(k+2),...
则这个序列第k点的:
一阶前向差分定义为: △ f ( k ) = f ( k + 1 ) − f ( k ) \bigtriangleup f(k)=f(k+1)-f(k) △f(k)=f(k+1)−f(k)
一阶后向差分定义为: ▽ f ( k ) = f ( k ) − f ( k − 1 ) \bigtriangledown f(k)=f(k)-f(k-1) ▽f(k)=f(k)−f(k−1)
从上面的定义来看,前向差分和后向差分其实没有本质上的区别,所以它们的性质也相同。
序列f(k)的二阶差分是对其一阶差分的差分,即:
△ 2 f ( k ) = △ [ △ f ( k ) ] = △ [ f ( k + 1 ) − f ( k ) ] = △ f ( k + 1 ) − △ f ( k ) \bigtriangleup ^{2} f(k)=\bigtriangleup [\bigtriangleup f(k)]=\bigtriangleup [f(k+1)-f(k)]=\bigtriangleup f(k+1)-\bigtriangleup f(k) △2f(k)=△[△f(k)]=△[f(k+1)−f(k)]=△f(k+1)−△f(k)
= f ( k + 2 ) − 2 f ( k + 1 ) + f ( k ) =f(k+2)-2f(k+1)+f(k) =f(k+2)−2f(k+1)+f(k)
用通俗的话来讲:差分,其实就是下一个数值 ,减去上一个数值 。用下一个数值,减去上一个数值 ,就叫“一阶差分”,对一阶差分的结果再做一次差分,就叫“二阶差分"。
从上面的定义式我们可以看出:
对于序列的前向差分,其最后一个点是没有一阶差分的,其最后两个点是没有二阶差分的。
对于序列的后向差分,其第一个点是没有一阶差分的,其第一个点和第二个点是没有二阶差分的。
那么怎么利用序列的差分运算寻找序列的下降沿、上升沿、极值点(波峰、波谷)呢?
离散序列的差分运算类似于连续函数中的求导运算,所以对比上面连续函数对极值点判定的充分条件,我们可以探索出对离散序列下降沿、上升沿、极值点(波峰、波谷)的找寻方法。具体方法如下:
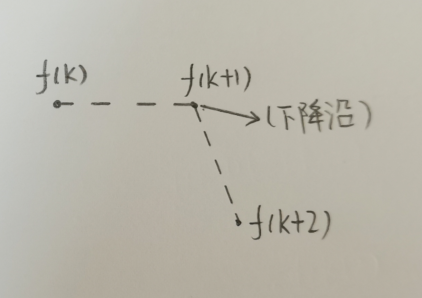
情况一:寻找下降沿
设离散序列中序号为k的点满足以下条件:
① △ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0
② △ f ( k + 1 ) < 0 \bigtriangleup f(k+1)<0 △f(k+1)<0
则序号为k+1的点是一个下降沿。
证明:
因为 △ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0,所以有 f ( k + 1 ) − f ( k ) = 0 f(k+1)-f(k)=0 f(k+1)−f(k)=0,所以 f ( k + 1 ) = f ( k ) f(k+1)=f(k) f(k+1)=f(k)
又由于 △ f ( k + 1 ) < 0 \bigtriangleup f(k+1)<0 △f(k+1)<0
所以 △ f ( k + 1 ) = f ( k + 2 ) − f ( k + 1 ) < 0 \bigtriangleup f(k+1)=f(k+2)-f(k+1)<0 △f(k+1)=f(k+2)−f(k+1)<0
综上,有 f ( k ) = f ( k + 1 ) > f ( k + 2 ) f(k)=f(k+1)>f(k+2) f(k)=f(k+1)>f(k+2)
所以第k+1个点是一个下降沿的边缘。
此时相关点的位置关系如下图所示:
情况二:寻找上升沿
设离散序列中序号为k的点满足以下条件:
① △ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0
② △ f ( k + 1 ) > 0 \bigtriangleup f(k+1)>0 △f(k+1)>0
则序号为k+1的点是一个上升沿。
证明:
因为 △ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0,所以有 f ( k + 1 ) − f ( k ) = 0 f(k+1)-f(k)=0 f(k+1)−f(k)=0,所以 f ( k + 1 ) = f ( k ) f(k+1)=f(k) f(k+1)=f(k)
又由于 △ f ( k + 1 ) > 0 \bigtriangleup f(k+1)>0 △f(k+1)>0
所以 △ f ( k + 1 ) = f ( k + 2 ) − f ( k + 1 ) > 0 \bigtriangleup f(k+1)=f(k+2)-f(k+1)>0 △f(k+1)=f(k+2)−f(k+1)>0
综上,有 f ( k ) = f ( k + 1 ) < f ( k + 2 ) f(k)=f(k+1)<f(k+2) f(k)=f(k+1)<f(k+2)
所以第k+1个点是一个上升沿的边缘。
此时相关点的位置关系如下图所示:
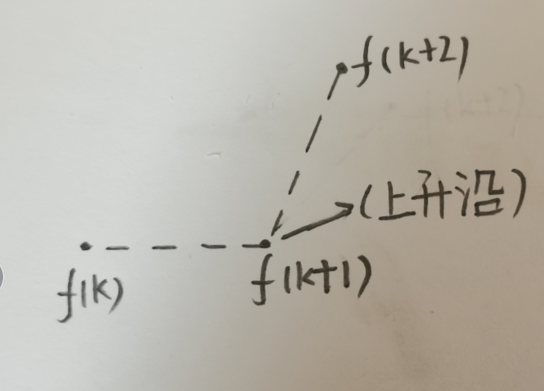
情况三:寻找极大值点
设离散序列中序号为k的点满足以下条件:
△ f ( k − 2 ) > 0 \bigtriangleup f(k-2)>0 △f(k−2)>0
△ f ( k − 1 ) = 0 \bigtriangleup f(k-1)=0 △f(k−1)=0
△ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0
△ f ( k + 1 ) < 0 \bigtriangleup f(k+1)<0 △f(k+1)<0
则序号为k的点是一个极大值点。
证明:略,参考情况一、情况二的证明。
此时相关点的位置关系如下图所示:
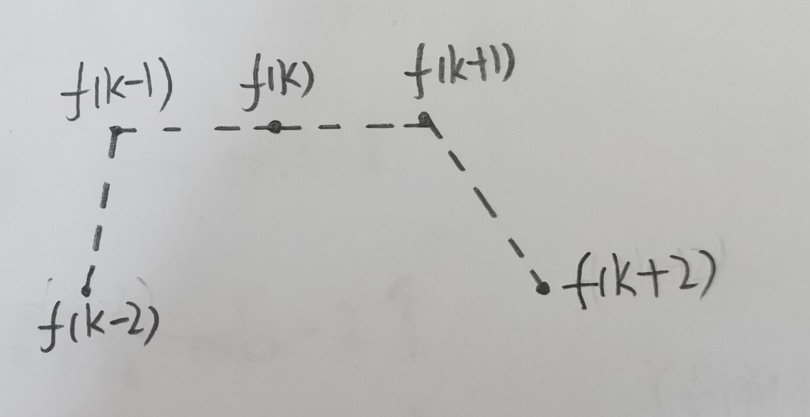
情况四:找寻极小值点
设离散序列中序号为k的点满足以下条件:
△ f ( k − 2 ) < 0 \bigtriangleup f(k-2)<0 △f(k−2)<0
△ f ( k − 1 ) = 0 \bigtriangleup f(k-1)=0 △f(k−1)=0
△ f ( k ) = 0 \bigtriangleup f(k)=0 △f(k)=0
△ f ( k + 1 ) > 0 \bigtriangleup f(k+1)>0 △f(k+1)>0
则序号为k的点是一个极小值点。
证明:略,参考情况一、情况二的证明。
此时相关点的位置关系如下图所示:
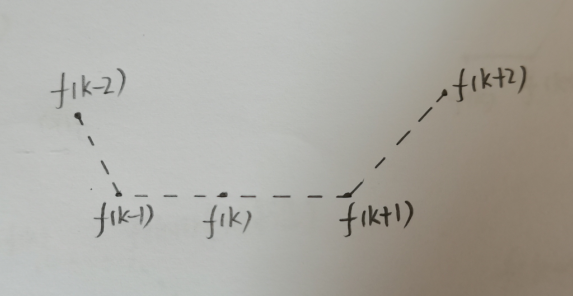
需要说明的两点:
①上面情况三、情况四的条件是充分条件,也就是说不满足上面情况的点也有可能是极大值点,极小值点。比如下面图中的k点,它是一个波峰,但它并不满足上面的判定条件。
②上面的判断条件中并没有用到前面介绍的二阶差分,那为什么要说二阶差分运算呢?因为刚好说到这个知识点,所以就多说了几句嘛。
下面这个链接是运用序列的差分运算找寻离散序列下降沿的例子:
https://www.hhai.cc/thread-232-1-1.html
这篇关于利用离散序列的差分运算寻找序列的下降沿、上升沿、极大值(波峰)、极小值(波谷)的原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








