【从零开始数学建模（2）】简单优化-存贮模型

前言

简单的优化模型，归结为微积分中的函数极值问题，可以直接用微分法求解。

用数学建模方法处理一个优化问题

• 确定优化目标是什么，寻求决策是什么，决策受到哪些条件限制
• 对实际问题作若干合理的简化假设、用数学工具（变量、常数、函数等）表示他们
• 在用微分法求出最优决策后，要对结果作出一些定性、定量分析和必要检验

---

不允许缺货 存储模型

问题情境：配件厂为装配线生产若干种部件，轮换生产不同的部件时因更换设备要付生产准备费（与生产数量无关），同一部件的产量大于需求时因积压资金、占用仓库要付贮存费用，现在已知某一部件的日需求量100键，生产准备费5000元，贮存费每日每件1元，如果生产能力远大于需求，并且不允许出现缺货，试安排该产品的生产计划，即多少天生产一次（称为生产周期），每次产量多少，可以使总费用最小。

---

问题分析

• 若每天生产1次，每次100件，无贮存费，生产准备费5000元，每天费用5000元；
• 若10天生产1次，每次1000件，贮存费  元，生产准备费5000元，总计9500元，平均每天费用950元；
• 若50天生产1次，每次5000件，贮存费  元，生产准备费5000元，总计127500元，平均每天费用2550元；

        从上面的计算来看，生产周期端、产量少，会使贮存费小，准备费大；而周期长、产量多，会使贮存费大，准备费小。所以必然存在一个最佳的周期，使总费用最小。

        一般地，考察这样的不允许缺货的存贮模型：产品的需求稳定不变，生产准备费和产品贮存费为常数、生产能力无限、不允许缺货，确定生产周期和产量，使得总费用最小。

---

模型假设

        时间和产量为离散量，为了处理方便我们考虑连续模型，即设生产周期T与产量Q均为连续量。根据问题性质作出以下假设：

1. 产品每天的需求量为常数 .
2. 每次生产准备费  ，每天每件产品的贮存费  .
3. 生产能力为无限大（相对于需求量），当贮存量降为零时， 件产品立即生产出来供给需求，即不允许出现断货。

---

模型建立

将贮存量表示为时间t的函数  ， 生产  件，贮存量 ， 以需求速率  递减，直到  ，如图1，显然有

（1）

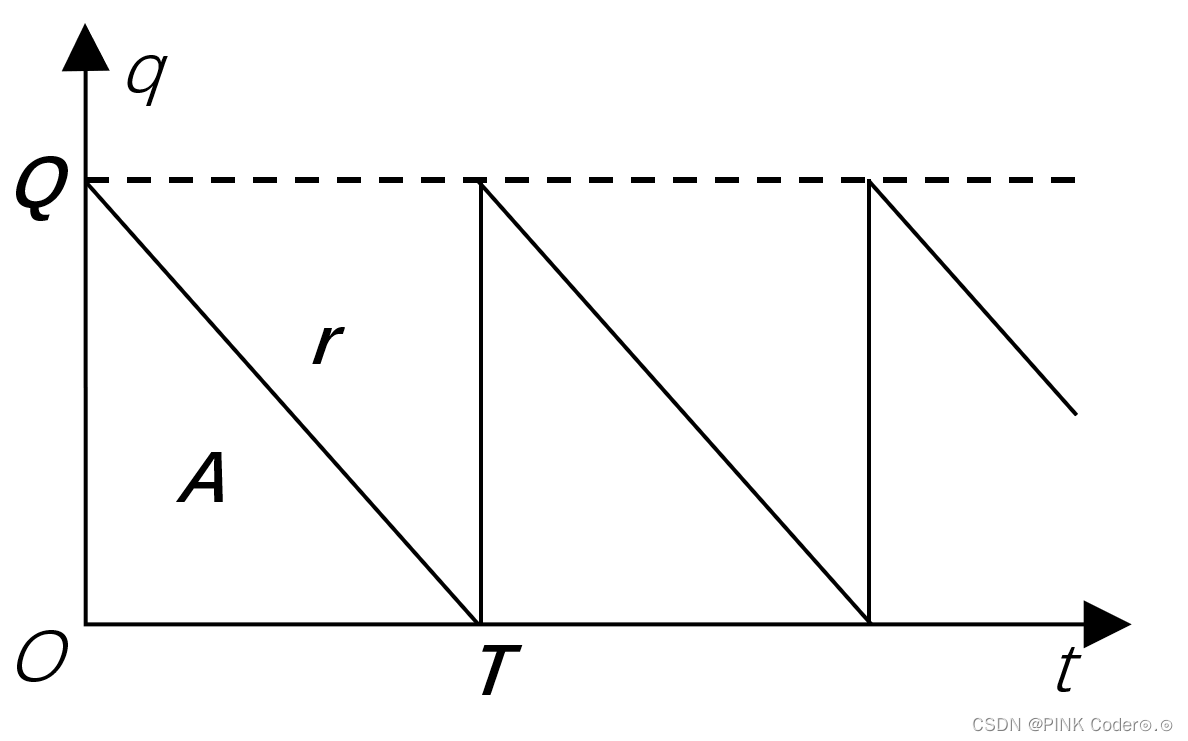
一个周期内的贮存费是  ，其中的积分恰等于图1中三角形A的面积  ，因为一个周期的准备费是  ，再注意到（1）式，等到一个周期的总费用为

 

                                 （2）

于是每天的费用为：

                    （3）

（3）式为这个优化模型的目标函数。

---

模型求解

求  使得（3）式的  最小，容易得到

                                          （4）

代入（1）式可得

              （5）

由（3）式算出最小的总费用为

                                                          （6）

（4）、（5）式是经济学中著名的经济订货批量公式（EOQ公式）

---

结果解释

        由（4）、（5）式可以看到，当准备费  增加时，生产周期和产量都变得大；当贮存费  增加时，生产周期和产量都变得小；当需求量  增加时，生产周期变小而产量变大。这些定性结果都是符合常识的。

        用得到的模型计算开始的问题：以  代入（4）（6）式可得到 天， 元，这里得到的  与之前计算的  有微小的误差的原因来自于将离散模型简化成连续模型，当各变量取较大数值时，误差会越来越小。

---

敏感性分析

讨论参数  有微小变化时对生产周期  的影响。

用相对该变量衡量结果对参数的敏感程度， 对  的敏感度记作 ，定义为

（7）

由（4）式容易得到  . 类似的可得到 ，.

即  增加1%， 增加0.5%，而  或  增加1%， 减少0.5%。 参数  有微小变化时对生产周期  的影响是很小的。

---

允许缺货 存储模型

        在某些情况下用户允许短时间的缺货，虽然这会造成一定的损失，但是如果损失费不超过不允许缺货导致的准备费和贮存费的话，允许缺货模型就应该是可以采取的策略。

---

模型假设

下面讨论一种简单的允许缺货模型：不允许缺货模型的假设1，2不变，假设3改为：

1. 产品每天的需求量为常数 .
2. 每次生产准备费  ，每天每件产品的贮存费  .
3. 生产能力为无限大（相对于需求量），允许缺货，每天每件产品缺货损失费为，但缺货数量在需在下次生产（或订货）时补足。

---

模型建立

因贮存量不足时造成缺货时，可认为贮存量函数  为负值，如图2.周期仍记作  ，  是每周期初的贮存量，当  时  ,于是有

（8）

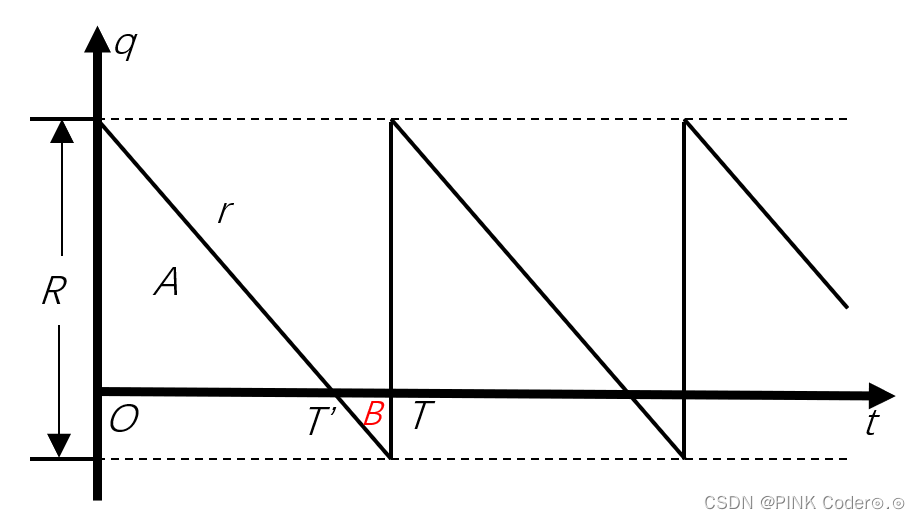
在  到  这段缺货时段内需求率  不变， 按原斜率继续下降。由于规定缺货量需补足，所以在  时数量为  的产品立即到达，使下周初的贮存量恢复到 。

与建立不允许缺货模型时类似，一个周期内的贮存费是  乘以图二三角形A的面积，缺货损失费则是  乘以图2中三角形B的面积。计算这两块面积，并加上准备费  ，得到一个周期内的总费用为

（9）

利用（8）式将模型的目标函数——每天的平均费用——记作  和  的二元函数 

（10）

---

模型求解

利用微分法求  和  使  最小，令   可得（区分不允许缺货，最优解记作 ，）

，

（11）

注意到每个周期的供货量 ，有

 

（12）

记

（13）

与不允许缺货模型（3）（4）比较不难得到

（14）

---

结果解释

由（13）式，，故（14）式给出  ，即允许缺货时周期及供货量的增加，周期初的贮存量减少，缺货损失费  越大（相对于贮存费 ）， 越小，越接近 ，， 越接近  。

特别的当  时 ，于是 ，，，缺货损失费  为无限大即是缺货的代价无限大，即可认为是第一种情况——不允许缺货存储模型。

由此可知不允许缺货模型可视作允许缺货模型的特例。

---

模型拓展

1）若在存贮模型中增加购买货物本身的费用，重新确定的最优订货周期和订货批量与原来保持一致，不论可否允许缺货，在（3）（10）两式只多了成本这个常数，不影响最值。
2）模型可拓展为生产销售模型，即开始的一段时间一边生产一边销售，后一段时间只销售不生产，（设第两阶段从T0开始，销售速率为r，生产速率为k）

---

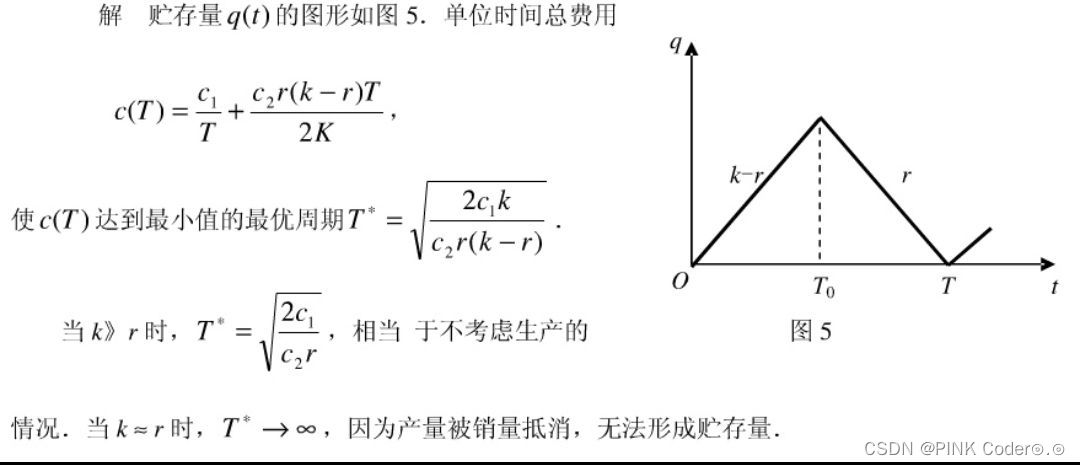
参考文献：姜启源 《数学模型》（第四版）