饼图，为何是数据界最被诟病的图表？

饼图（Pie Chart) 的每个切片代表整体的一部分，通常切片大小用于显示百分比，扇区的总和为100%。

但在数据可视化不断发展中，饼图被广为诟病为是最糟糕的展现形式之一。

当然还存在其他更冗杂和麻烦的数据展现形式，但饼图是广为公众熟悉的图表之一。文章接下来将分析饼图在数据可视化中的劣势以及可替代的图表。

饼图的缺点

缺点一：饼图不能详细展现每部分的细节情况

饼图的意义在于展现各部分相对于总体的关系。以下是三张饼图表示五个候选人在A，B，C三个时间段内的获票情况。

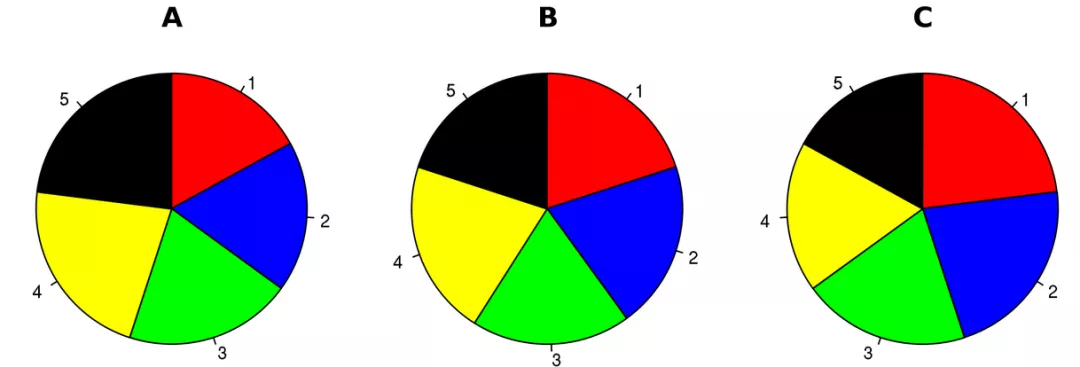
图表应该让读者明确看出每个候选人在不同时间段的得票比重，以及候选人之间的得票角逐。然而上述饼图展现出来的效果并非如此。无法通过上述饼图回答以下几点问题：

• 五号候选人和三号候选人相比，哪个表现更好？

• 在A和B时间段内，候选人二号和候选人四号，哪个表现更好？

• 哪位候选人在选票上领先？

如果图表的意义在于更容易解读信息，如果直接给投票数据表格，是否相比上述饼图更容易让读者获取信息呢？

同样的数据换一种展现方式——条形图——则清晰很多：

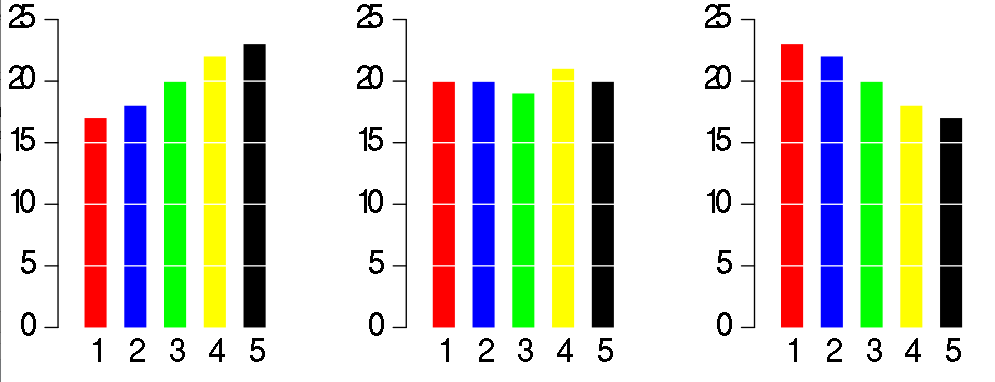
通过上述条形图，读者能直观到每个候选人在每个时间段的具体获票情况。即使饼图的意义就在于展现部分和整体关系，但上述条形图比饼图更加清晰展现出部分相对于整体的情况。

缺点二：违反视觉感知规律：人们并不能真正理解圆形和角度的大小

是否能从以下的饼图找出最大的一组，并按照值大小排序切片？答案可能是否定的。

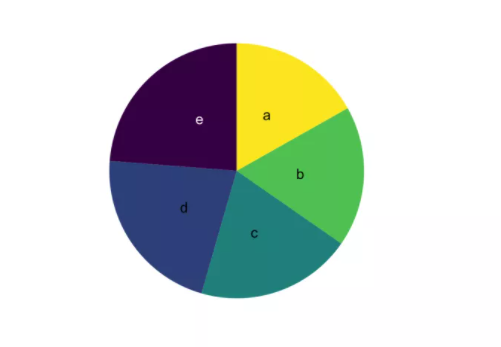
如果你仍然不信？那尝试通过以下饼图中辨别出哪个组的值最高，并且尝试弄清楚各组的数值变化过程。或许仍非常困难找出差异。

如果使用条形图表示完全相同的数据呢？

结果一目了然！正如条形图展现，三个饼图之间存在着巨大的差异。

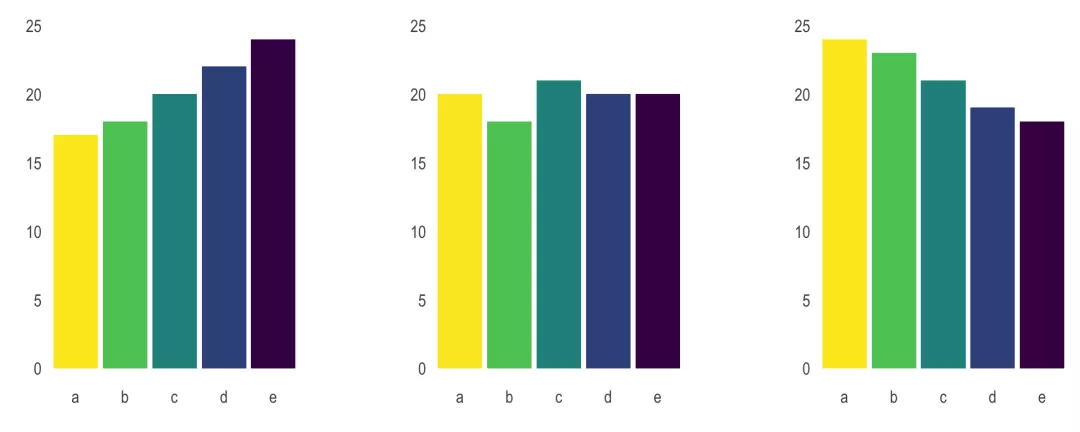
同理，以下这张饼图展现欧洲议会的党派的划分:

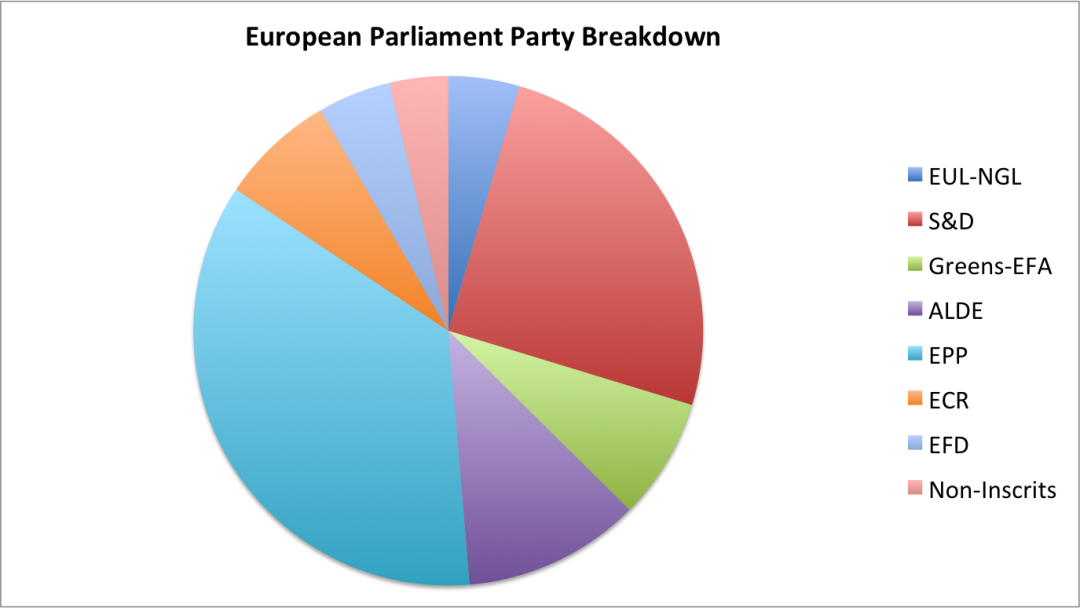
你是否可以通过比较切片找出每个切片之间的大小差异么？

如果仅针对这一个问题，那么确实可以。从以上饼图可知EPP党的份额大于S&D党。那么该饼图的重点又是什么？图表只有在我们能够比较其中每个元素的时候才有用。

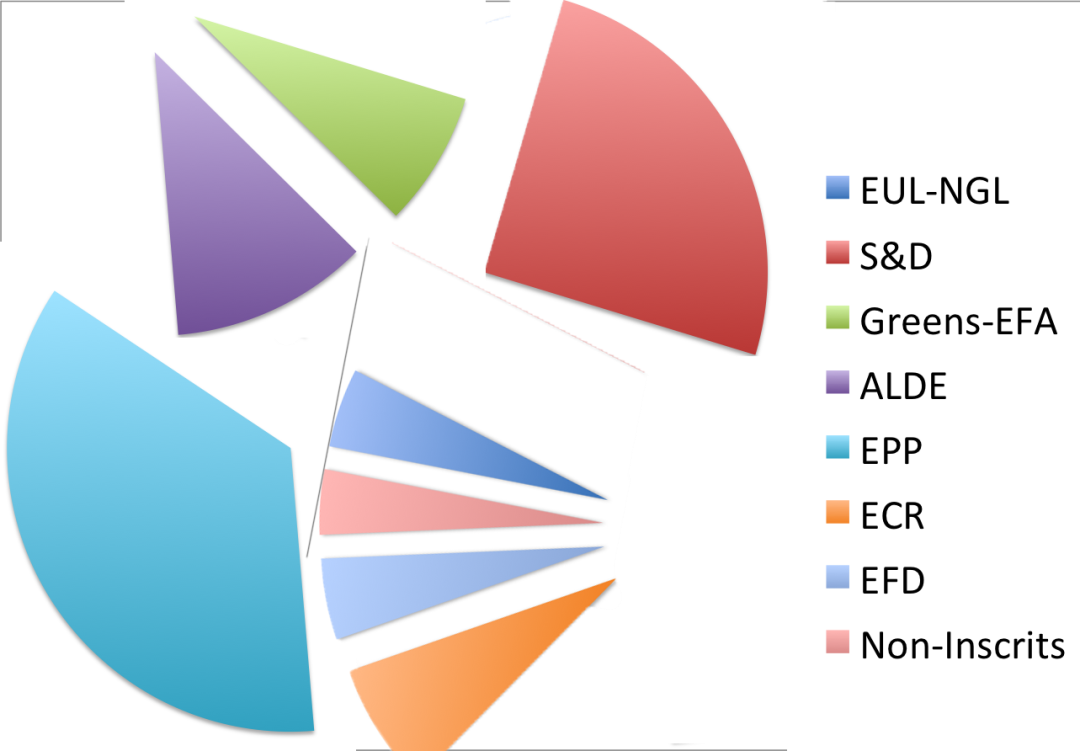
那么出于比较目的，我们单独脱离整体和文本对比单个切片。

事实证明，人们并不擅长通过比较饼图切片来衡量大小。这就是为什么人们会认为三角形学和弧度比矩形几何更难。

以下条形图同样展现党派细分信息：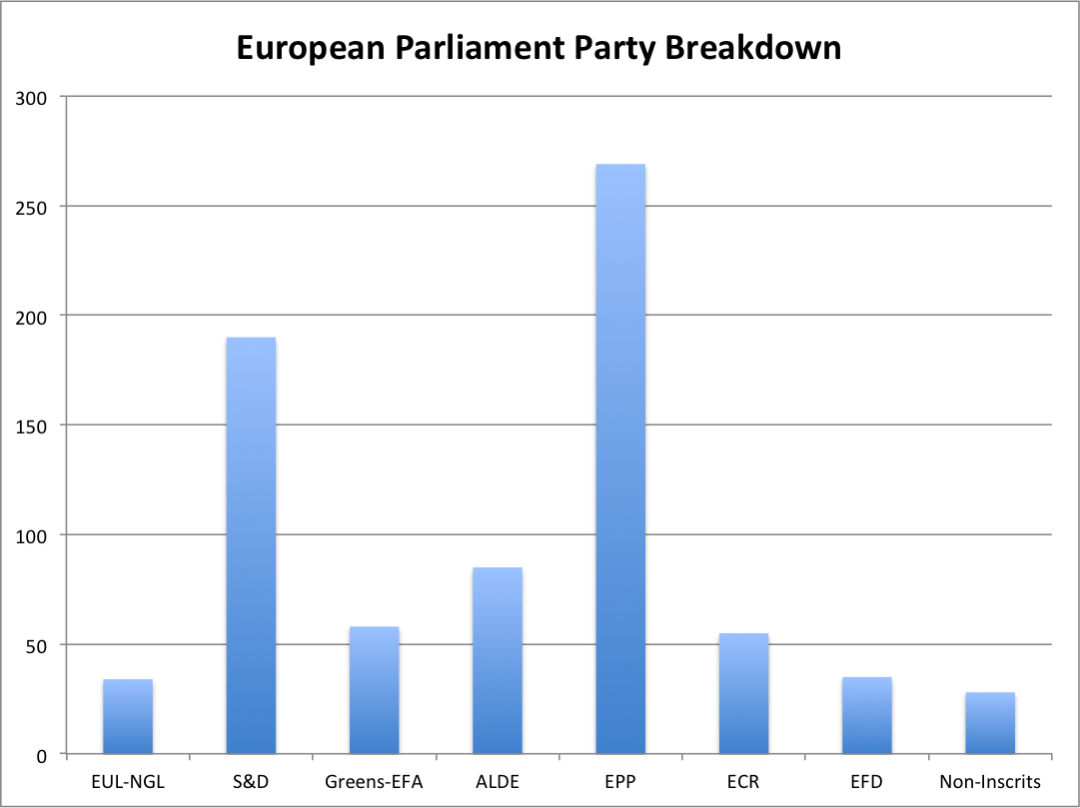
通常人们只会比较矩形的长度来了解数据的变化。若将左纵坐标轴改成百分比，读者可以得知议会内不同的党派分配。对比可见，条形图可以看到每个党派拥有多少席位，但此信息无法从饼图得知。

以下是同样的党派细分信息，但以3D饼图的效果呈现：

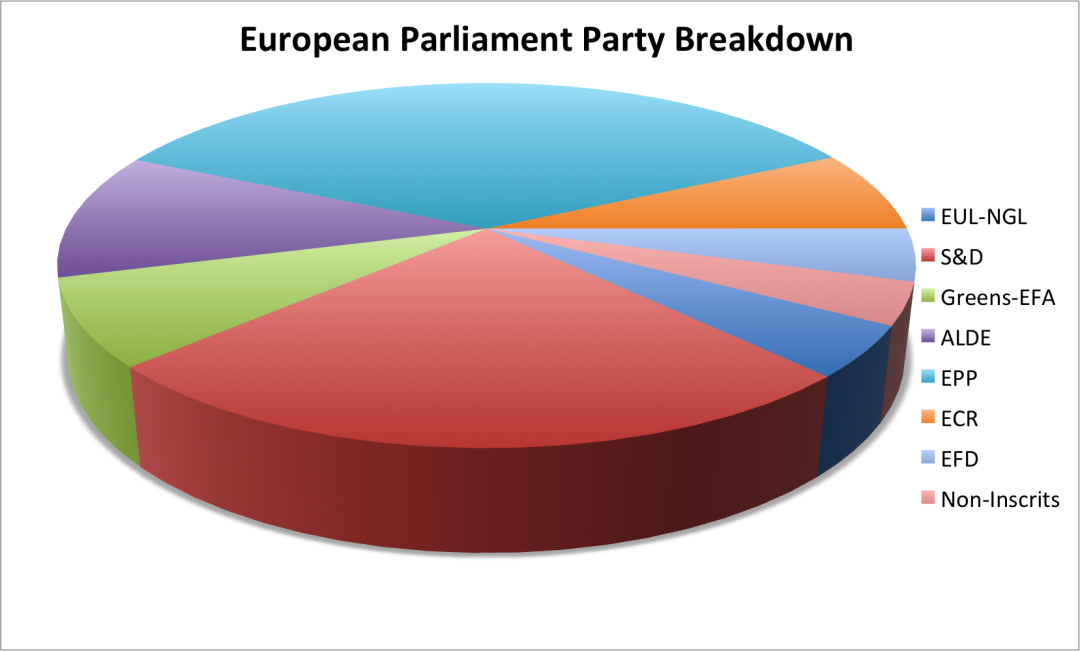
有角度的3D饼图非常能给出迷惑读者的信息！上述3D饼图中红方的S&D党似乎与深青色方的EPP党大致持平。然而这样的扭曲视觉的效果完全可以人为操作。

缺点三：依赖数据标签说明信息

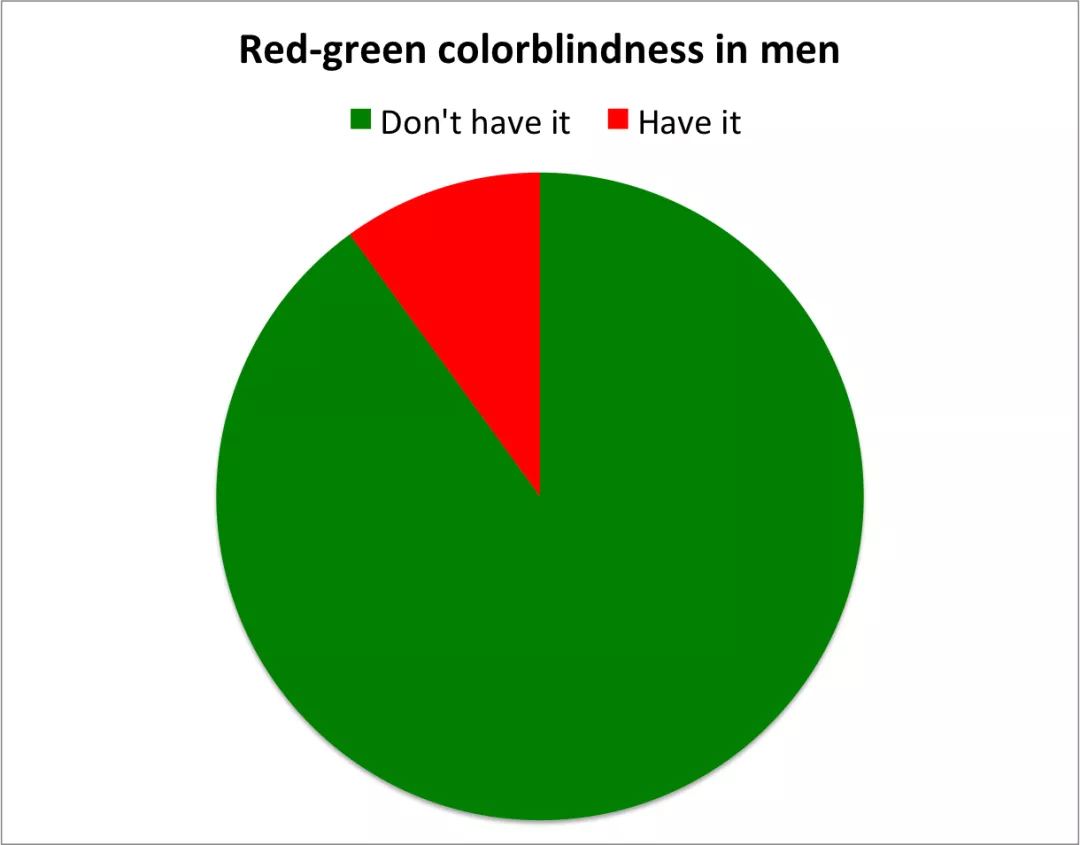
上述饼图旨在展现男性中红绿色盲的比例。但我们并不能由上述饼图直接得知男性色盲的占比约为10%。一般来说，越高级的图表越不需要数据标签。如果必须得依靠数据标签才能表达信息，大概率你则使用了错误的图表。

饼图的优势：

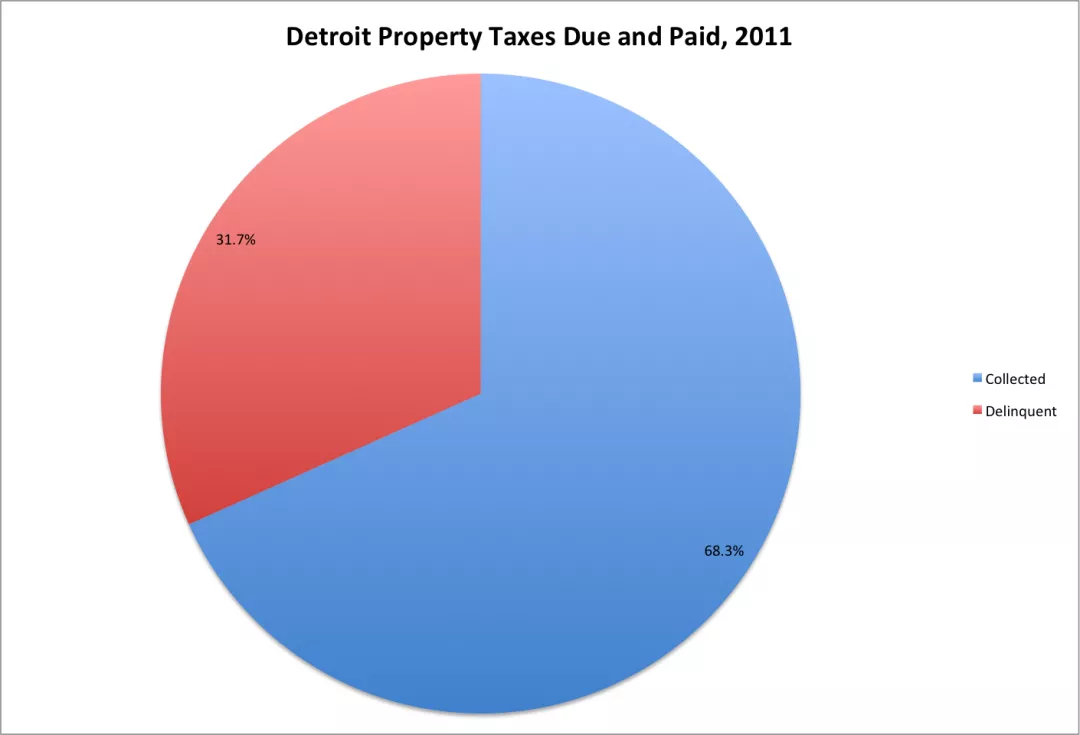
在对比2-3个具备较大差异的数据点时，饼图还是具备优势的。上述饼图表示的是底特律房产拖欠情况。上述图表能清晰告诉读者，100人中有32人是什么情况。

综上：
以下情况饼图不适合使用：

• 每当可用信息存在相似性时；

• 每当由多个（三个或者更多）不同数据点时；

• 如果必须标记每个数值的百分比才能读取信息时。

以下情况会让饼图更糟糕：

• 3D效果；

• 保留图例；

• 扇区各部分总和不足100的百分比；

• 过多数据点比较；

• 切割所有切片脱离整体单独对比（ExplodedPie Charts)。

那在我们得知饼图的优劣势，是否有其他替代饼图的图表呢？

条形图

如果有多个值需要展示，可以采用比柱状图更加优雅简洁的“棒棒糖图”（Lolipop Plot)。以下图展现几个代表国家出售武器的数量情况：

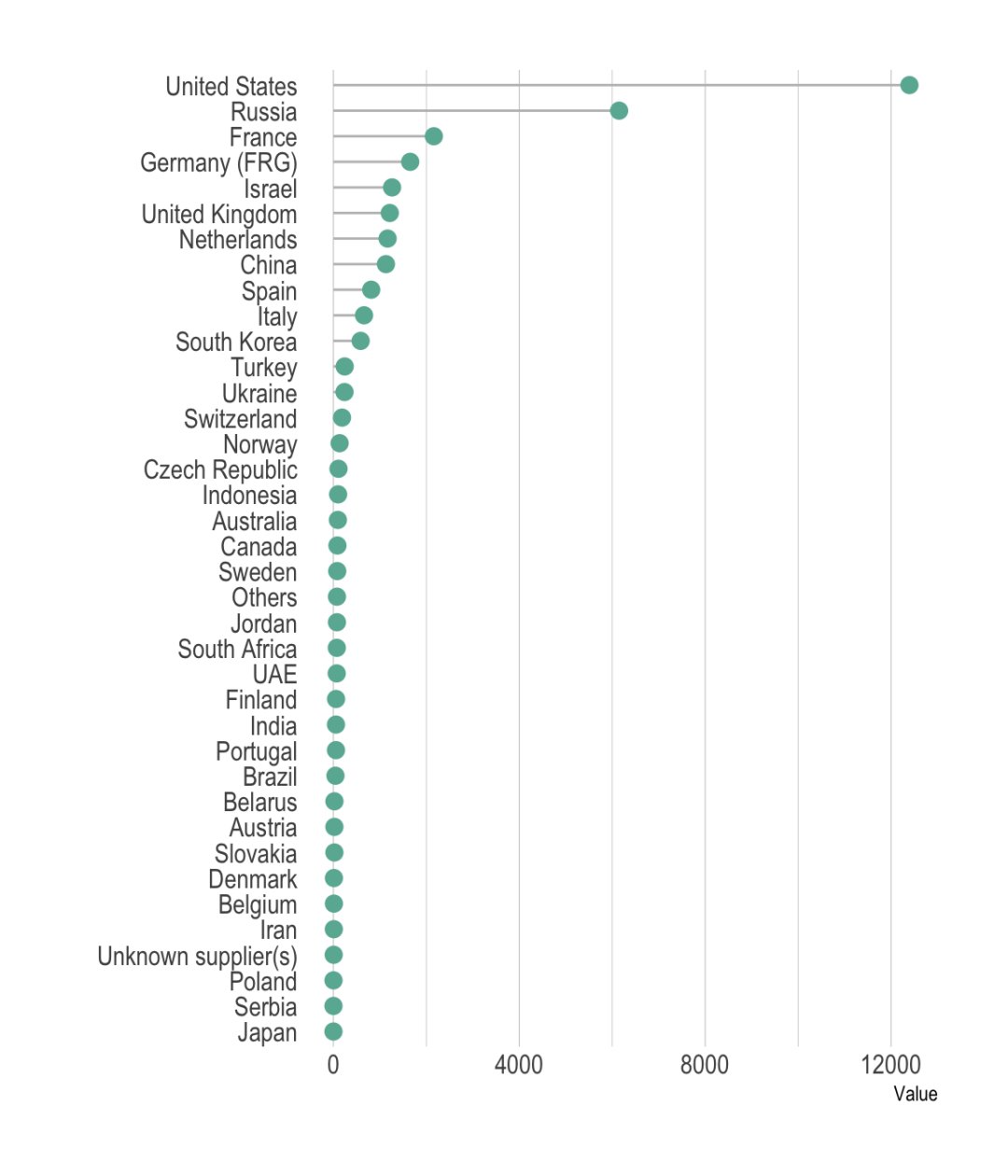
树状图

如果你想描述整体的组成情况，那么树状图是个不错的选择

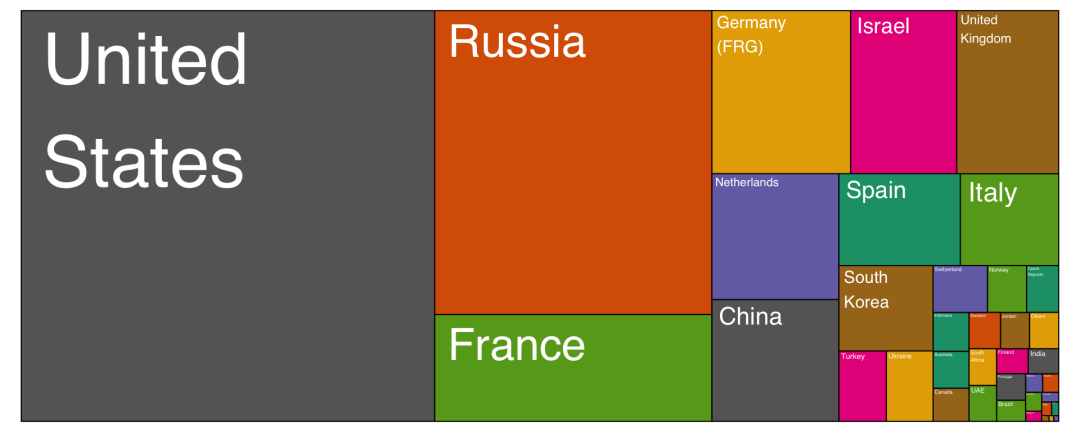
简而言之，在对比多个不同数据点或者必须依赖数据标记才能得知数据间相似性时，应该尽量避免使用饼图。饼图大多时不能达到理想的数据可视化的效果，而且视觉效果太容易被搞砸。因此，在使用饼图时，请多考虑是否能有可替代的图表呈现出更理想的效果。