omni rpc python生成地址_用 Python 讲解偏度和峰度

之前笔者在做一个金融数据项目时，有朋友问我，衡量股票收益率有没有什么好的方法。这个问题让笔者也思索了好久，其实股票的收益率如果我们从本质来看不就是数据吗，无非就是收益率我们就想让其越高越好，也就是让这个数据增加得越多越好。而衡量数据我们经常用到的方法有均值、方差、偏度和峰度。均值和方差是我们见到和用到最多的方法，甚至在中学课本里都有提及，那么笔者今天就讲一下偏度和峰度这两个大家不太常用的方法，并结合python代码讲一下偏度和峰度在数据分析中的简单应用。
首先还是介绍一下偏度和峰度的概念。

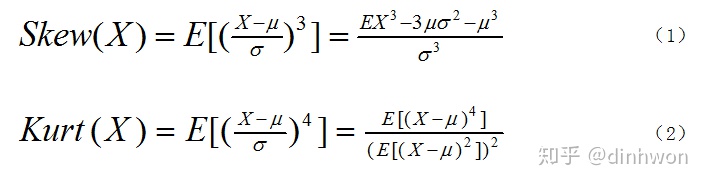
图1. 偏度和峰度公式
偏度（skewness）又称偏态、偏态系数，是描述数据分布偏斜方向和程度的度量，其是衡量数据分布非对称程度的数字特征。对于随机变量X，其偏度是样本的三阶标准化矩，计算公式如图1中的式（1）所示。
偏度的衡量是相对于正态分布来说，正态分布的偏度为0。因此我们说，若数据分布是对称的，偏度为0；若偏度>0，则可认为分布为右偏，也叫正偏，即分布有一条长尾在右；若偏度<0，则可认为分布为左偏，也叫负偏，即分布有一条长尾在左。正偏和负偏如图2所示，在图2中，左边的就是正偏，右边的是负偏。

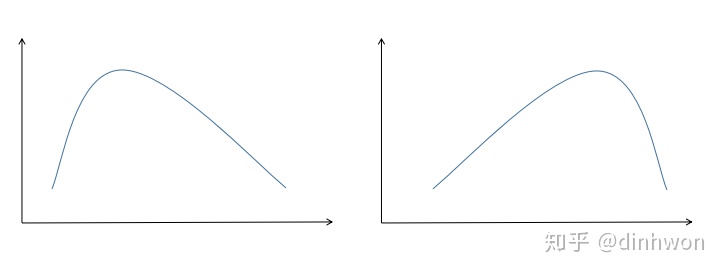
图2. 偏度的示意图
而峰度（Kurtosis）则是描述数据分布陡峭或平滑的统计量，通过对峰度的计算，我们能够判定数据分布相对于正态分布而言是更陡峭还是平缓。对于随机变量X，其峰度为样本的四阶标准中心矩，计算公式如图1中的式2所示。
当峰度系数>0，从形态上看，它相比于正态分布要更陡峭或尾部更厚；而峰度系数<0，从形态上看，则它相比于正态分布更平缓或尾部更薄。在实际环境当中，如果一个分部是厚尾的，这个分布往往比正态分布的尾部具有更大的“质量”，即含又更多的极端值。我们常用的几个分布中，正态分布的峰度为0，均匀分布的峰度为-1.2，指数分布的峰度为6。
峰度的示意图如图3所示，其中第一个子图就是峰度为0的情况，第二个子图是峰度大于0的情况，第三个则是峰度小于0。

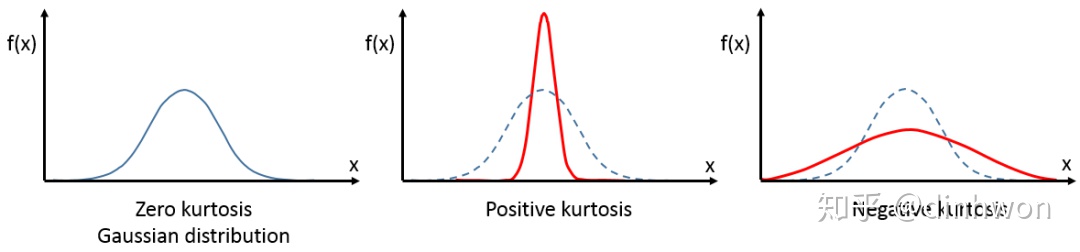
图3. 峰度的示意图
在说完基本概念之后，我们就再讲一下怎么基于偏度和峰度进行正态性检验。这里主要有两种方法，一是Omnibus检验，二是Jarque - Bera检验。

图4. Omnibus和JB检验的公式
Omnibus检验的公式如图4中公式（3）所示，式中Z1和Z2是两个正态化函数，g1和g2则分别是偏度和峰度，在Z1和Z2的作用下，K的结果就接近于卡方分布，我们就能用卡方分布来检验了。这个公式的原理比较复杂，大家如想了解可自行查找相关资料。
Jarque - Bera检验的公式如图4中公式（4）所示，式中n是样本量，这个结果也是接近于卡方分布，其原理也不在这里赘述。这两个检验都是基于所用数据是正态分布的，即有如下假设。
原假设H0：数据是正态分布的。
备择假设H1：数据不是正态分布。
下面我们用代码来说明一下偏度和峰度。
首先看一下数据，这个数据很简单，只有15行2列。数据描述的是火灾事故的损失以及火灾发生地与最近消防站的距离，前者单位是千元，后者单位是千米，数据如图5所示。其中distance指火灾发生地与最近消防站的距离，loss指火灾事故的损失。

图5. 数据示例
下面是代码，首先导入需要的库。import pandas as pdimport matplotlib.pyplot as pltimport statsmodels.stats.api as smsimport statsmodels.formula.api as smffrom statsmodels.compat import lzipfrom statsmodels.graphics.tsaplots import plot_acf
接下来是读取数据并作图，这些代码都非常简单，笔者不做过多的解释。
file = r'C:Usersdata.xlsx'
df = pd.read_excel(file)
fig, ax = plt.subplots(figsize=(8,6))
plt.ylabel('Loss')
plt.xlabel('Distance')
plt.plot(df['distance'], df['loss'], 'bo-', label='loss')
plt.legend()
plt.show()
结果如图6所示，从结果中我们可以看到这些点大致在一条直线上，那么我们就用一元线性回归来拟合这些数据。

图6. 数据连线图
下面是生成模型，并输出模型的结果。
expr = 'loss ~ distance'
results = smf.ols(expr, df).fit() #生成回归模型
print(results.summary())
结果如图7所示。从图中我们可以看到，Prob (F-statistic)的值为1.25e-08，这个值非常小，说明我们的一元线性回归模型是正确的，也就是loss和distance的线性关系是显著的。而图中还可以看到Skew=-0.003，说明这部分数据非常接近正态分布，而Kurtosis=1.706，说明我们的数据比正态分布更陡峭，是一个尖峰。此外，从图中还可以看到Omnibus=2.551，Prob(Omnibus)=0.279，Jarque-Bera (JB)=1.047，Prob(JB)=0.592，这里我们很难直接从Omnibus和Jarque-Bera的数值来判断是否支持前面的备择假设，但我们可以从Prob(Omnibus)和Prob(JB)这两个数值来判断，因为这两个数值都比较大，那么我们就无法拒绝前面的原假设，即H0是正确的，说明我们的数据是服从正态分布的。

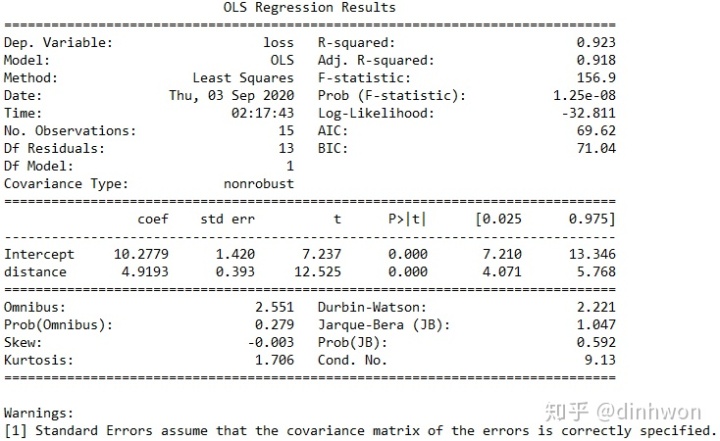
图7. 模型结果说明
接下来我们再验证一下Skew、Kurtosis、Omnibus和Jarque-Bera (JB)这些数值，用的是statsmodels自带的方法。代码如下。
omnibus_label = ['Omnibus K-squared test', 'Chi-squared(2) p-value']
omnibus_test = sms.omni_normtest(results.resid) #omnibus检验
omnibus_results = lzip(omnibus_label, omnibus_test)
jb_label = ['Jarque-Bera test', 'Chi-squared(2) p-value', 'Skewness', 'Kurtosis']
jb_test = sms.jarque_bera(results.resid) #jarque_bera检验
jb_results = lzip(jb_label, jb_test)
print(omnibus_results)
print(jb_results)
这里omnibus_label和jb_label是两个list，里面包含了我们所要检验的项目名称，sms.omni_normtest就是statsmodels自带的omnibus检验方法，sms.jarque_bera就是statsmodels自带的jarque_bera检验方法。results.resid是残差值，一共有15个值，我们的数据本身就只有15个点，这里的每个残差值就对应前面的每个数据点，sms.omni_normtest和sms.jarque_bera就是通过残差值来进行检验的。而lzip这个方法很少见，其用法和python中原生函数zip差不多，笔者在这里更多地是想让大家了解statsmodels，所以用了lzip，这里直接用zip也是可以的，至于lzip和zip的区别，留给大家自行去学习。而上面得到的结果如图8所示。从图8中可以看到，我们得到的结果和前面图7中的结果一模一样。这里用sms.omni_normtest和sms.jarque_bera来进行验证，主要是对前面图7中的结果的一个解释，帮助大家更好地学习statsmodels。

图8. omnibus和jb检验的结果
本文主要通过statsmodels来解释一下偏度和峰度在数据分析中的一些基本应用，想要更深入了解偏度、峰度以及statsmodels的读者，可以自行查阅相关资料。