五一快乐加餐（动态规划）4题综合版（每日更新5.3已更）

 1.五（背包)

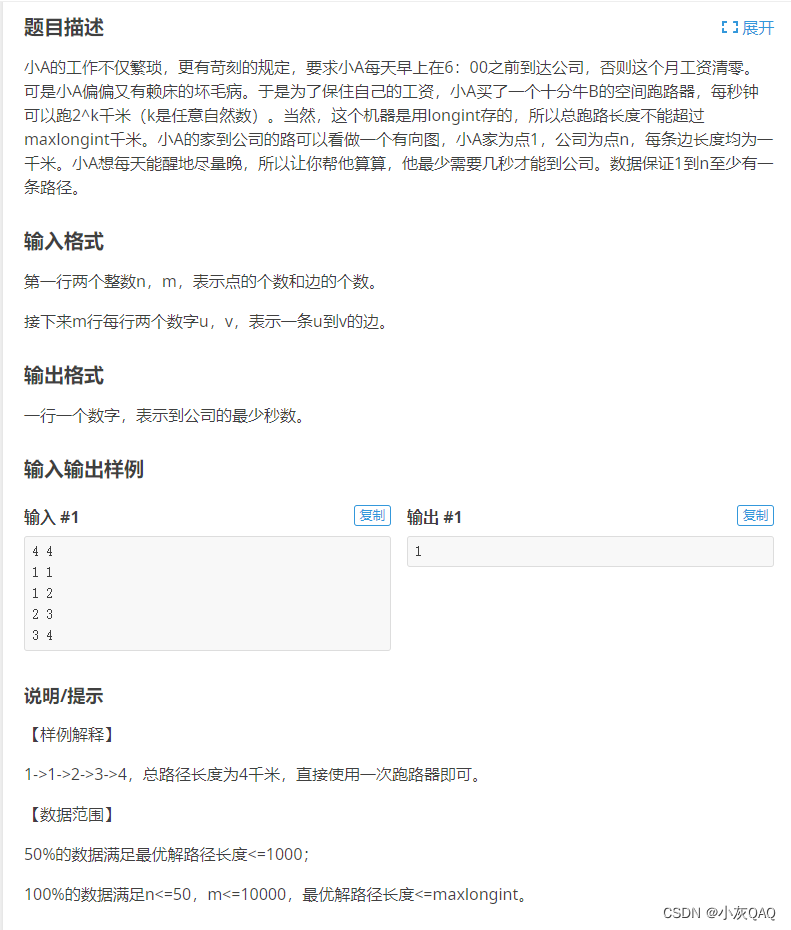
 解题思路：背包问题，通过每一步的局部最优解，来找到最优解。

#include<iostream>
#include<algorithm>
using namespace std;
int w[30],v[30],f[50000];//w数组为重要度，v数组为money，f是用来dp的数组
int n,m;//n是总物品个数，m是总钱数
int main()
{cin>>m>>n;//输入for(int i=1;i<=n;i++){cin>>v[i]>>w[i];w[i]*=v[i];//w数组在这里意义变为总收获（重要度*money）}//01背包（参照第二类模板“一维数组优化”）for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--)//注意从m开始{if(j>=v[i]){f[j]=max(f[j],f[j-v[i]]+w[i]);//dp}}}cout<<f[m]<<endl;//背包大小为m时最大值return 0;
} 

2.一（背包

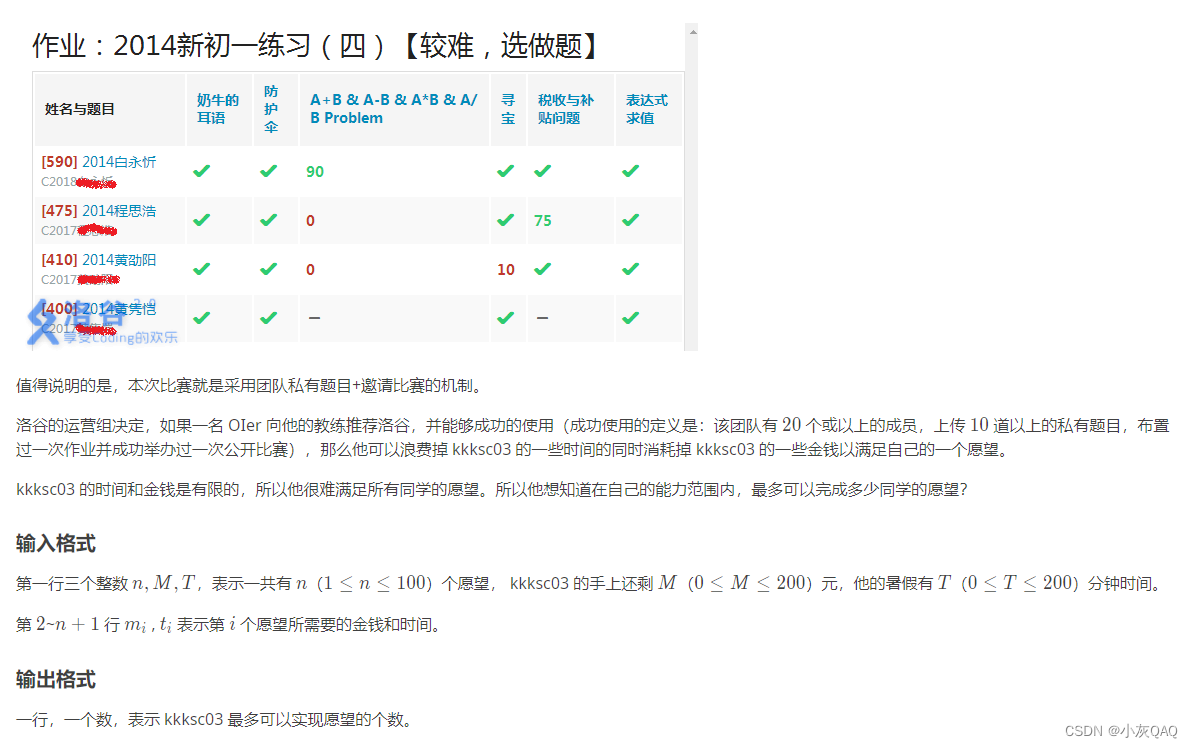
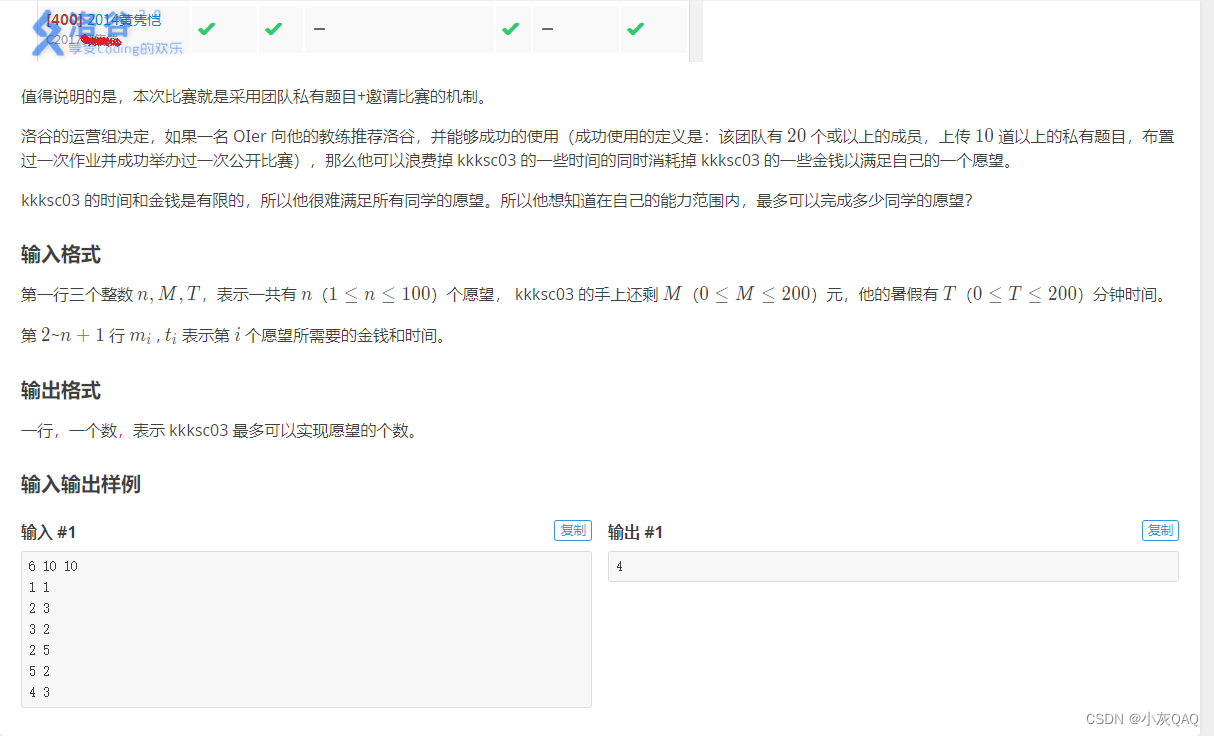
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,M,T,dp[1010][1010];
int m[1010],t[1010];
int main()
{scanf("%d%d%d",&n,&M,&T);for(int i=1;i<=n;i++){//仅仅只是多了一维而已 scanf("%d%d",&m[i],&t[i]);for(int j=M;j>=m[i];j--)for(int k=T;k>=t[i];k--){dp[j][k]=max(dp[j][k],dp[j-m[i]][k-t[i]]+1);}}printf("%d\n",dp[M][T]);
}

3.乐（线性

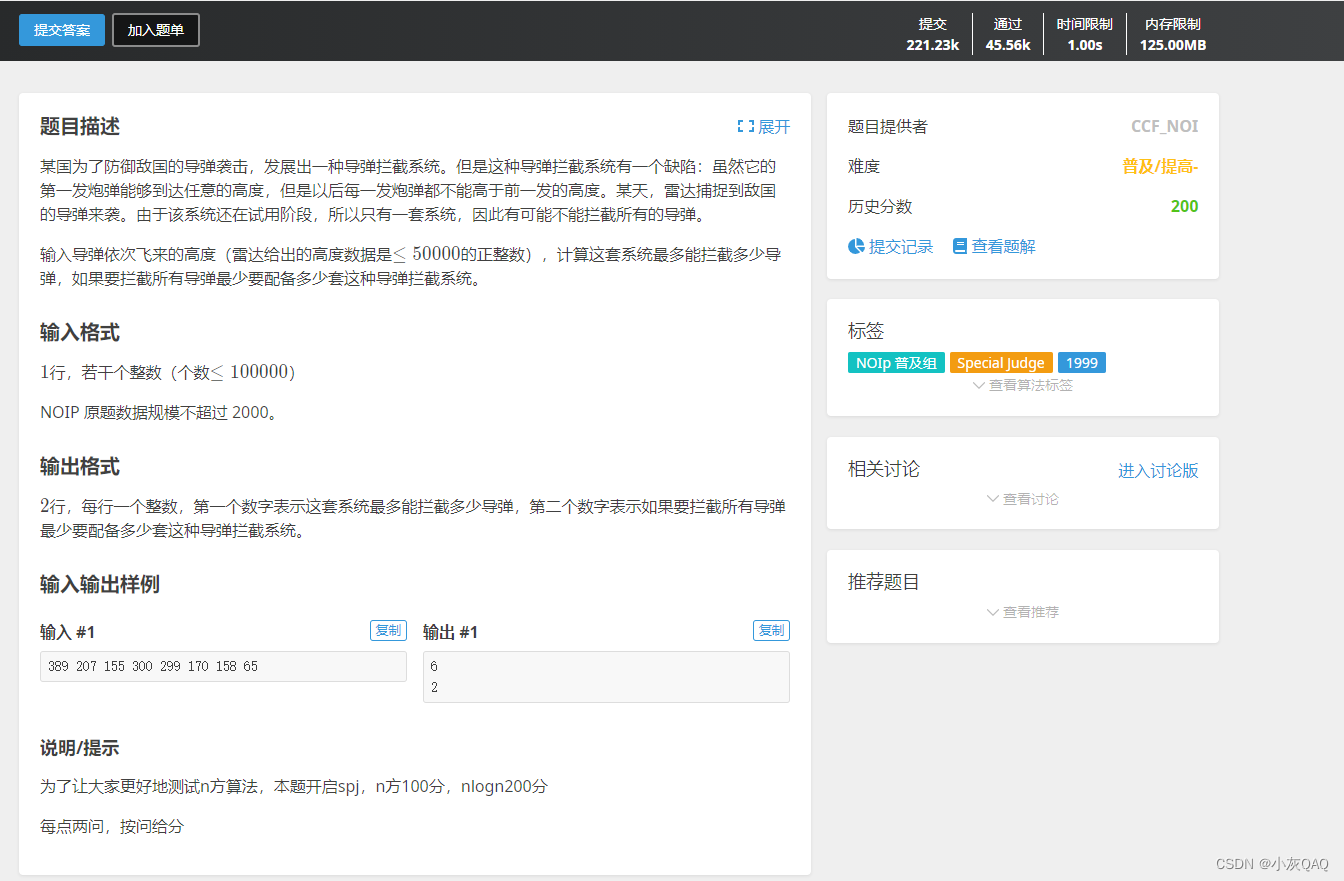
思路： 
先从后往前循环，计算出 该数 的最长不上升子序列，记录下来，开始下一个数，不需一个个去查找，只要满足比往后的一个数大，就直接判断是该数的序列长度+1（至于为什么+1，代码上解释）长还是本身长。

389 207 155 300 299 170 158 65

以这组样例为例，看一下表格。

第二问用最长不下降子序列的长度回答即可

| | i=8 | i=7 |i=6 | i=5 | i=4 | i=3 | i=2 |i=1 | | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | -----------: | |f[1]| 0 | 0 | 0 | 0 | 0| 0 | 0| 6 | |f[2] |0 | 0 |0 |0 |0 |0 |4 | 4| | |f[3] | 0 |0 | 0 | 0 | 0| 2 |2 | 2| |f[4]|0 |0 | 0 |0 | 5| 5 | 5| 5 |f[5] |0 | 0 | 0| 4 | 4| 4 | 4| 4
|f[6] | 0 | 0 |3 | 3 | 3| 3 | 3|3| |f[7] | 0 | 2 | 2| 2| 2| 2 | 2|2 | |f[8] | 1 | 1 | 1| 1| 1| 1 | 1|1|

f[i]为第i个数字到最后一个数字的最长不上升子序列。

#include<bits/stdc++.h>
using namespace std;
int n=0;
int a[100005],f[100005];
int main(){while(scanf("%d",&a[++n])!=EOF);//输入方式--n;//注意，要n--int s=0;//拦截导弹数量for(int i=n;i>=1;i--) //从后往前算{f[i]=1;//初始第一个可以拦for(int j=i+1;j<=n;j++)//往n进行循环，计算i~n的最长不上升子序列if(a[i]>=a[j])//如果满足条件不上升{f[i]=max(f[i],f[j]+1);//注意，f[j]一定要+1，1为能拦截的第一个导弹即a[i]这发导弹。s=max(f[i],s);//求最大值}cout<<s;s=0;for(int i=n;i>=1;i--) //同上{f[i]=1;for(int j=i+1;j<=n;j++)if(a[i]<a[j])//因为是求最长不下降子序列{f[i]=max(f[i],f[j]+1);}s=max(f[i],s);}cout<<' '<<s;return 0;
}