2019MathorCup数学建模挑战赛D题 钢水 “脱氧合金化”配料方案的优化

钢水“脱氧合金化”配料方案的优化

首先这道题给的附件一很不整齐，应该进行数据预处理。最好是处理成那种行列都有的一个方方的矩阵形式，就比如说你平常练机器学习代码给的那种数据一样，是删还是补都行，保证数据准确，对后面模型建立很重要。

问题一

要求计算$C、Mn$两种元素的历史收得率，这个用$Excel$在后面加个一列套个公式就能算出来。这个计算公式是
$$X收得率=\frac{连铸正样\times (钢水净重+合金重量)-转炉终点\times 钢水净重}{加入X元素重量}$$

然后问影响其收得率的主要因素，这里用了因子分析。

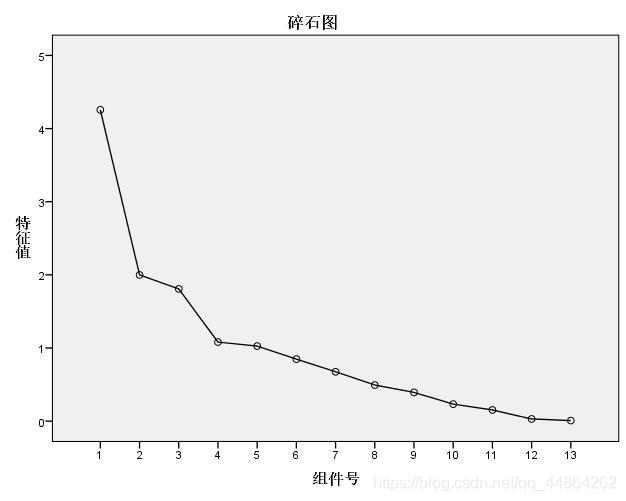
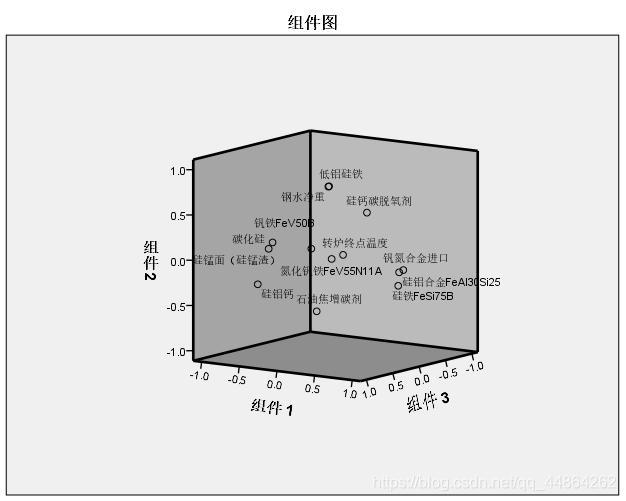
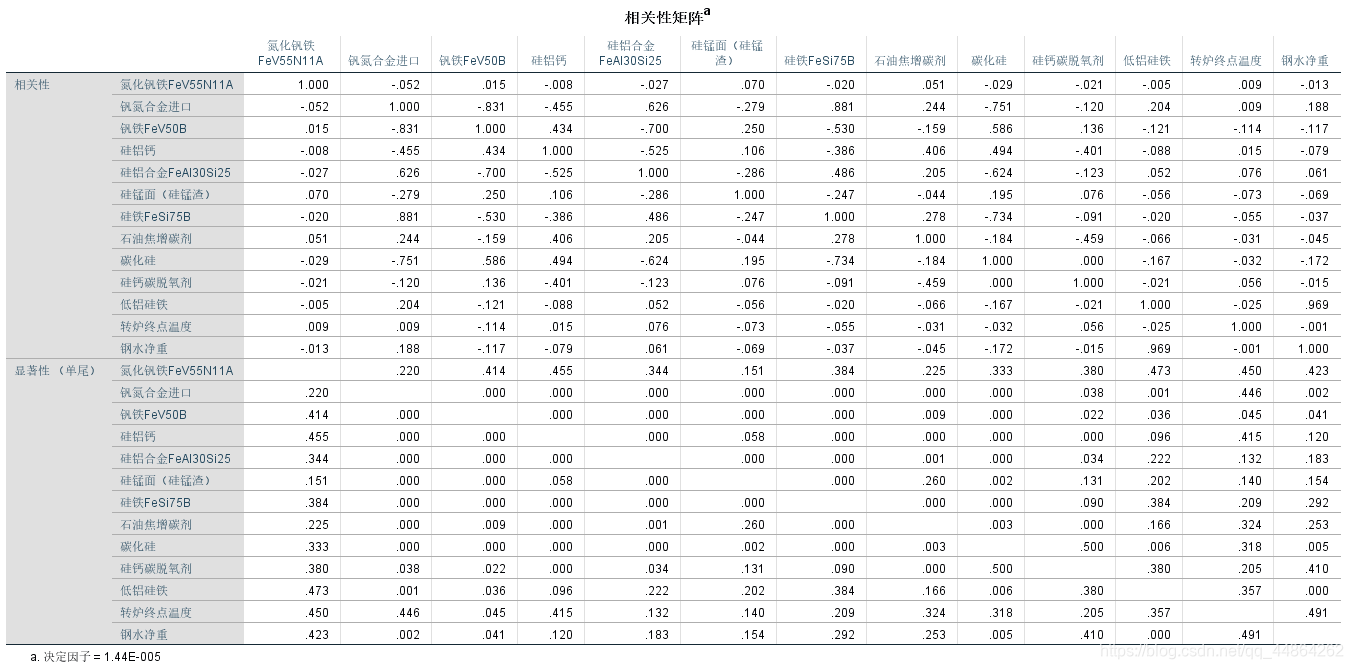
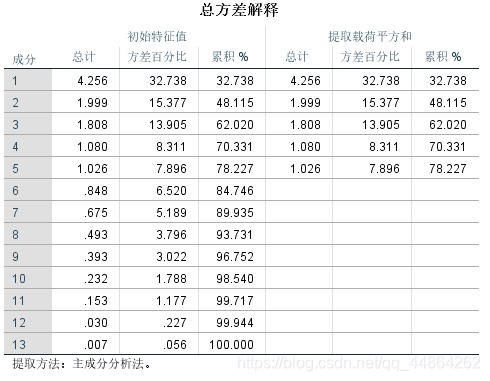
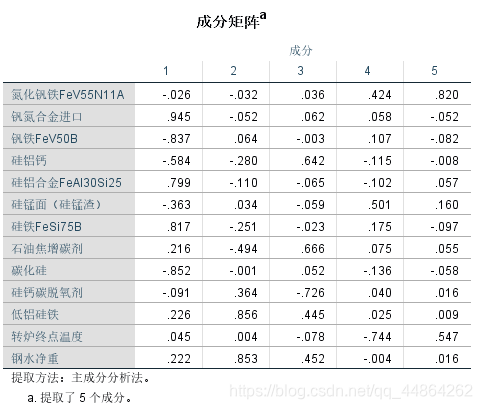
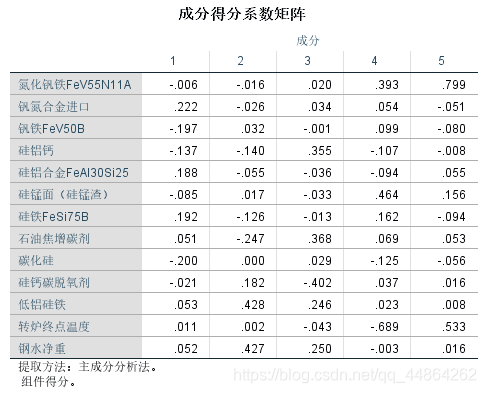
问题二

支持向量回归

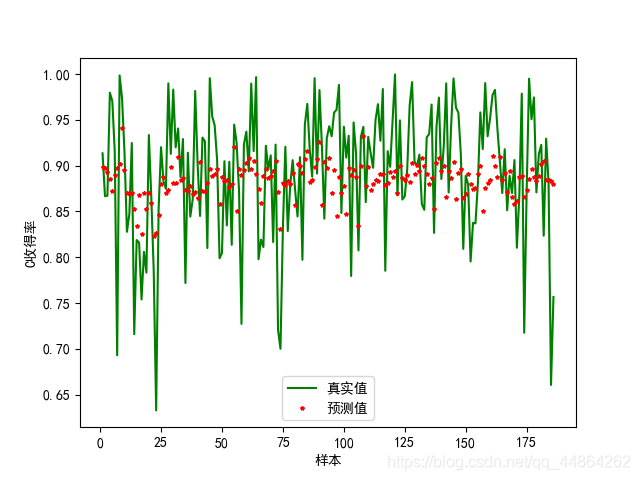
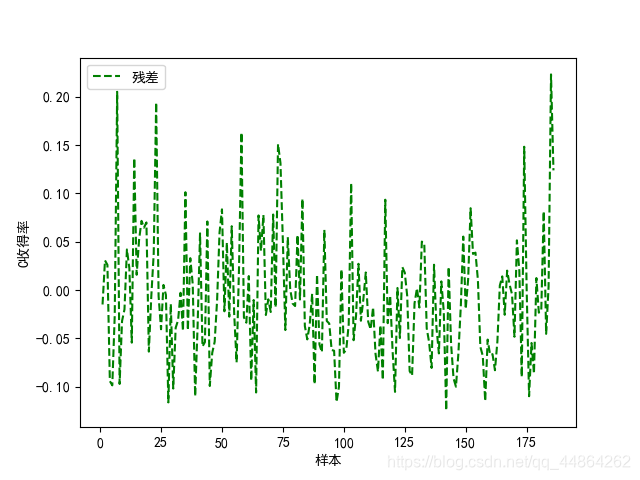
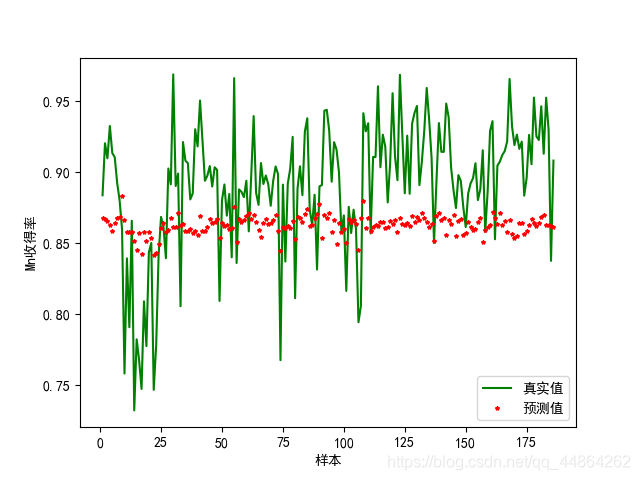
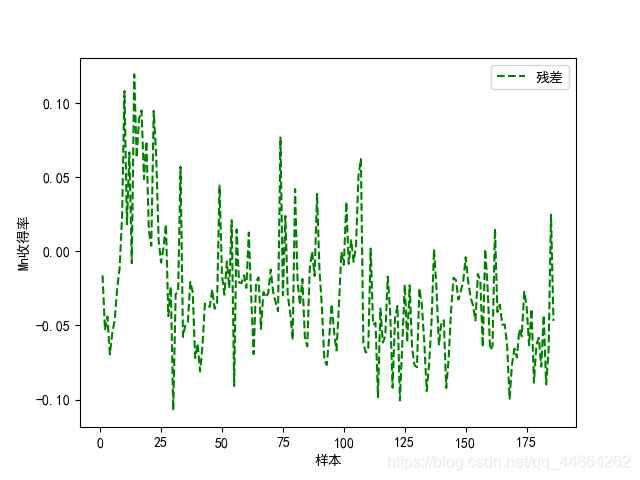
Python支持向量回归代码实现

import pylab as plt
from sklearn.svm import SVR
import numpy as np
from numpy import array, loadtxtplt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
a = loadtxt('problem2.txt')
x0 = a[:, :7]
y1 = a[:, 7]
model = SVR()
model.fit(x0,y1)
x_np_list = np.arange(1, len(y1) + 1, 1)
plt.plot(x_np_list,y1, c="green",label='真实值')
plt.plot(x_np_list,model.predict(x0),'r*',markersize=3,label='预测值')
plt.xlabel('样本')
plt.ylabel('C收得率')
plt.legend()
plt.show()
y_di_list = model.predict(x0) - y1
sum = 0
for i in y_di_list:sum = sum + i**2
print('残差和为：',sum)
plt.plot(x_np_list,y_di_list,'g--',label='残差')
plt.xlabel('样本')
plt.ylabel('C收得率')
plt.legend()
plt.show()
a = loadtxt('problem2.txt')
x0 = a[:, :7]
y1 = a[:, 8]
model = SVR()
model.fit(x0,y1)
x_np_list = np.arange(1, len(y1) + 1, 1)
plt.plot(x_np_list,y1, c="green",label='真实值')
plt.plot(x_np_list,model.predict(x0),'r*',markersize=3,label='预测值')
plt.xlabel('样本')
plt.ylabel('Mn收得率')
plt.legend()
plt.show()
y_di_list = model.predict(x0) - y1
sum = 0
for i in y_di_list:sum = sum + i**2
print('残差和为：',sum)
plt.plot(x_np_list,y_di_list,'g--',label='残差')
plt.xlabel('样本')
plt.ylabel('Mn收得率')
plt.legend()
plt.show()

对收得率进行预测，在第一问你挑出的几个主要因子做个预测模型，BP神经网络

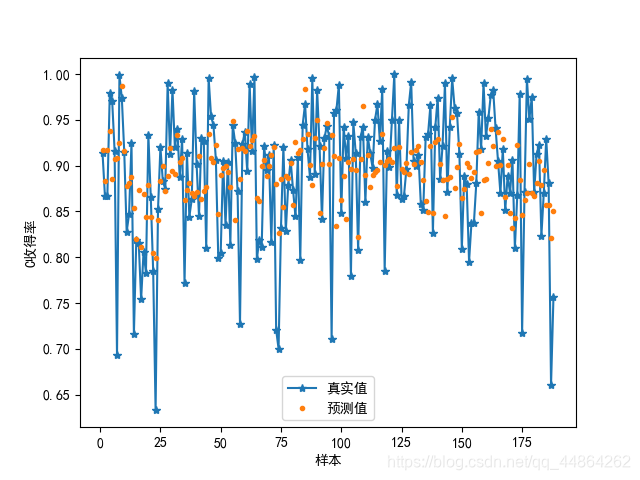
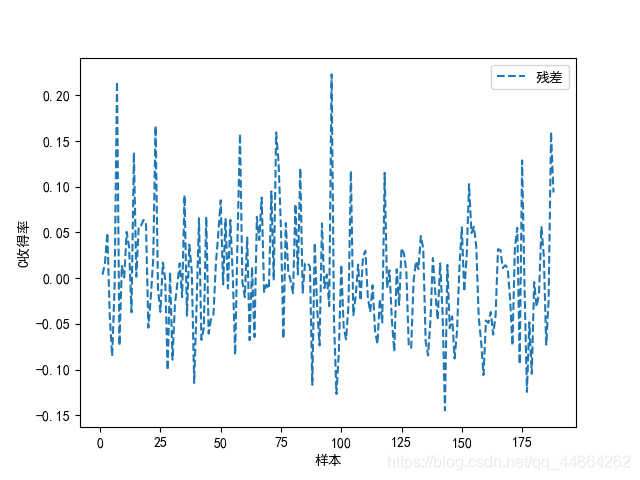
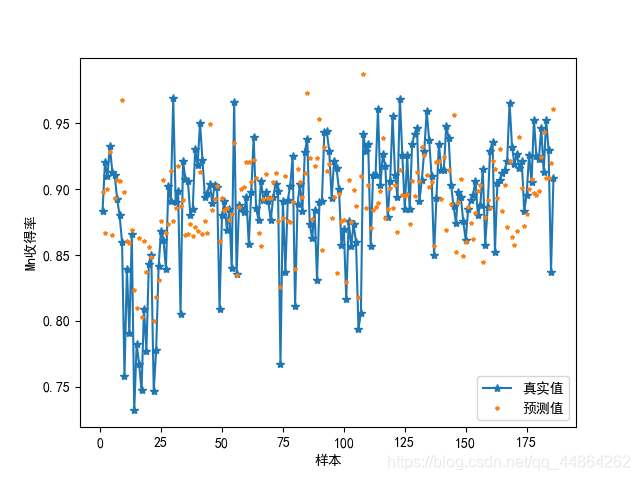
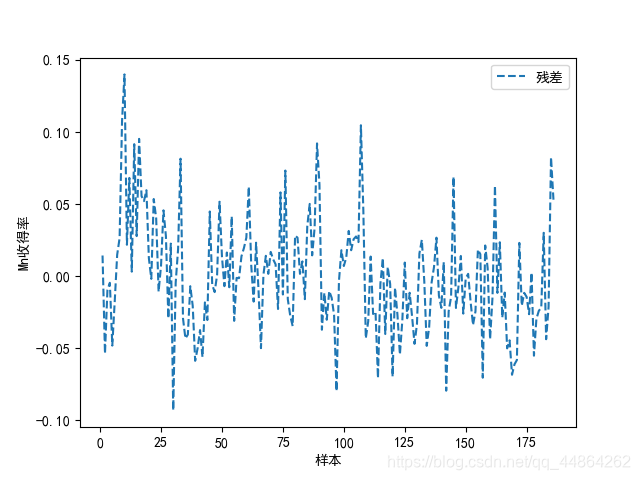
Python神经网络代码实现

from sklearn.neural_network import MLPRegressor
from numpy import loadtxt
import numpy as np
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
a = loadtxt('problem2.txt')
x0 = a[:, :7]
y1 = a[:, 7]
x_np_list = np.arange(1, len(y1) + 1, 1)
md1 = MLPRegressor(solver='lbfgs',alpha=1e-5,hidden_layer_sizes=500)
md1.fit(x0, y1)
plt.plot(x_np_list,y1,'-*',label='真实值')
plt.plot(x_np_list,md1.predict(x0),'*',markersize=3,label='预测值')
plt.xlabel('样本')
plt.ylabel('C收得率')
plt.legend()
plt.show()
y_di_list = md1.predict(x0) - y1
sum=0
for i in y_di_list:sum = sum + i**2
print('残差和为：',sum)
plt.plot(x_np_list,y_di_list,'--',label='残差')
plt.xlabel('样本')
plt.ylabel('C收得率')
plt.legend()
plt.show()
x0 = a[:, :7]
y1 = a[:, 8]
x_np_list = np.arange(1, len(y1) + 1, 1)
md1 = MLPRegressor(solver='lbfgs')
md1.fit(x0, y1)
plt.plot(x_np_list,y1,'-*',label='真实值')
plt.plot(x_np_list,md1.predict(x0),'*',markersize=3,label='预测值')
plt.xlabel('样本')
plt.ylabel('Mn收得率')
plt.legend()
plt.show()
y_di_list = md1.predict(x0) - y1
sum=0
for i in y_di_list:sum = sum + i**2
print('残差和为：',sum)
plt.plot(x_np_list,y_di_list,'--',label='残差')
plt.xlabel('样本')
plt.ylabel('Mn收得率')
plt.legend()
plt.show()
print(md1.score(x0,y1))

问题三

选因子做个规划模型，这里挑几个主要因子就可以
目标函数 成本最小
s.t. 所有元素的总含量都必须满足在内控区间内

from scipy.optimize import linprogk = 0.01
p = []
c = [350, 6.5, 350, 205, 11.8, 0.1, 8.5, 7.6, 6, 4.6, 8.15, 6.1, 4]
for i in c:a = i * kp.append(a)
A = [[0, 0, 0, 0.0031, 0, 0.00374, 0, 0.017, 0.0006, 0.96, 0.017, 0.3, 0.225692],[0, 0, 0, -0.0031, 0, -0.00374, 0, -0.017, -0.0006, -0.96, -0.017, -0.3, -0.225692],[0, 0.74, 0, 0.012, 0.341, 0.285, 0.3, 0.072, 0.767, 0, 0.172, 0.56, 0.392],[0, -0.74, 0, -0.012, -0.341, -0.285, -0.3, -0.072, -0.767, 0, -0.172, -0.56, -0.392],[0, 0, 0, 0, 0, 0, 0.3, 0.664, 0, 0, 0.664, 0, 0],[0, 0, 0, 0, 0, 0, -0.3, -0.664, 0, 0, -0.664, 0, 0],[0, 0, 0, 0.0006, 0, 0, 0, 0.0018, 0.0004, 0, 0.0018, 0, 0],[0, 0, 0, 0.0002, 0, 0, 0, 0.0002, 0.0002, 0, 0.0002, 0.0001, 0]]b = [[20040], [-15240], [52040], [-40040], [128000], [-104040], [3640], [3640]]
bounds = (
(0, None), (0, None), (0, None), (0, None), (0, None), (0, None), (0, None), (0, None), (0, None), (0, None), (0, None),
(0, None), (0, None))
res = linprog(p, A, b, None, None, bounds)print('目标函数的最小值为：', res.fun)
print('最优解为：', res.x * k)

问题四

我们通过一些了解得知，随着钢铁行业中高附加值钢种产量的不断提高，如何通过历史数据对脱氧合金化环节建立数学模型，在线预测并优化投入合金的种类及数量，在保证钢水质量的同时最大限度地降低合金钢的生产成本是各大钢铁企业提高竞争力所要解决的重要问题。而目前为止，国内大部分炼钢车间仅按照不同元素的固定收得率或经验值计算各种合金的加入量，难以实现当前炉次合金配料的自动优化和成本控制。因此我们针对这一问题建立了数学模型，实现对合金收得率较为准确的预测，并建立了成本最小模型，得以实现合金配料的自动优化和成本控制，下面是我们通过模型运算得出的建议…

word版论文+Python源代码

建模学习记录，存在错误敬请批评指正