upc 个人训练赛第四场：黑匣子+选地址（优先队列+弗洛伊德最短路）

问题 A: 13号星期几

题目描述
请编程统计：从1900年1月1日(当天是星期一）开始经过的n年当中，每个月的13号这一天是星期一、星期二、星期三、……、星期日的次数分别是多少？
输入
共一行，一个整数n (1≤n≤400)。
输出
仅一行， 有7个整数（依次是星期一、星期二、星期三、……、星期日的次数），各数间以空格相隔，行尾不能有多余的空格。
样例输入 Copy
1
样例输出 Copy
1 3 1 2 2 2 1

思路：
定义一个x，让他从1号开始循环，如果加一大于当前月份的值，就结束当前月份的循环，循环的同时判断对7取余的值，相应的余数开一个数组然后++即可

int n,x,t;
int a[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int vis[10];//记录周一到周天是13号的次数
int judge(int y)
{if((y%4 == 0 && y%100 != 0) || (y%400 == 0))return 1;else    return 0;
}int main()
{cin >> n;for(int i=1900;i<1900+n;i++){if(judge(i))    a[2]++;else    a[2] = 28;for(int j=1;j<=12;j++)//月份{x = 0;while(1){if(x+1 > a[j])   break;x++;t = (t+1)%8;if(t == 0)  t = 1;if(x == 13) vis[t]++;}}}for(int i=1;i<=7;i++)printf("%d ",vis[i]);printf("\n");return 0;
}

问题 B: 高兴的小明

题目描述
今天，小明很高兴，因为国庆放假了，又恰逢是自己的生日。为了庆祝节日，小明与邻居的小伙伴共n个人相约一起放花炮。他们先同时放响了第一个花炮，随后n个人分别以A1、A2、A3、……An秒的间隔继续放花炮，到最后每人都放了b个花炮（包括第一个）。问：总共可听到多少声花炮响？
输入
共三行，第一行仅一个整数n(n<=10)，第二行是A1、A2、A3、……An共n个整数(每个数<=100,各数间以空格相隔)，第三行只有一个整数b(b<=100)。
输出
仅一行，一个整数（听到的花炮响声数），行尾不能有多余的空格。
样例输入 Copy
3
1 2 3
4
样例输出 Copy
7

思路：
首先第一个花炮是同时放的，所以只能听到一次声响，即从ans = 1开始，之后观察数据发现，每个人放花炮听到声响其实就是一个等差数列，给出的间隔就是公差，同时在同一时间放出的花炮只能听见一次声响，问题就解决了
我一开始想用数组直接记录下放花炮的时间，最后发现还需要去重，于是我就想到了另外一种办法，可以直接让放花炮的时间做数组的下标，如果能听到就标记为1，这样就不容易出错了

int n,b,ans,cnt;
int a[15],c[10005];
int main()
{cin >> n;for(int i=1;i<=n;i++)    cin >> a[i];cin >> b;for(int i=1;i<=n;i++){for(int j=1;j<=b-1;j++){c[j*a[i]] = 1;}}ans = 1;for(int i=1;i<=10000;i++){if(c[i] == 1)   ans++;}cout << ans << endl;return 0;
}

问题 C: 摘彩球

题目描述
今年是国庆60周年，学校少先队大队部举行了庆祝活动，其中有一项活动是摘彩球。大队辅导员在学校礼堂里高低不一地挂了N个彩球，请M位少先队员到礼堂里摘彩球。辅导员说：你们每人最多可以摘两个彩球，而且只许站着伸手摘，不允许借助其它工具，摘下的彩球归大家共有。由于各少先队员的身高参差不齐，怎样才能使他们摘的彩球总数最多呢？请你计算少先队员们最多能摘到多少个彩球？
输入
第一行有二个整数N 和M(N<=100,M<=20)，两数间用空格隔开。
第二行有 N个整数（各数间以空格相隔），分别表示每个彩球的高度。
第三行有M个整数（各数间以空格相隔），分别表示每个少先队员伸手能达到的高度。
输出
仅一行，有一个整数，表示最多能摘到的彩球数，行尾不能有多余的空格。
样例输入 Copy
10 4
110 100 150 90 100 135 160 88 130 140
120 100 110 80
样例输出 Copy
5

思路：
这个题我先排序然后去掉了根本就够不到的彩球，然后循环比较大小，一旦彩球可以被摘下来，就把彩球的高度变为1，循环过程中不断判断ans % 2，如果为0，结束本次循环

int n,m,x,ans,cnt;
int a[105],b[25];
bool cmp(int x,int y)
{return x > y;
}int main()
{cin >> n >> m;for(int i=1;i<=n;i++)    cin >> a[i];for(int i=1;i<=m;i++)    cin >> b[i];sort(a+1,a+1+n,cmp);//降序 sort(b+1,b+1+m,cmp);for(int i=1;i<=n;i++){if(b[1] < a[i])  a[i] = 0;}//去掉根本够不到的 for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if((b[i] >= a[j]) && (a[j] != 0)){ans++;a[j] = 0;if(ans%2 == 0)  break;}}}cout << ans << endl;return 0;
}

问题 D: 莱布尼茨三角形

题目描述
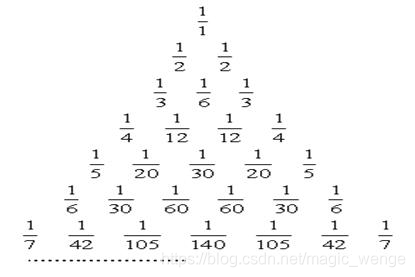
世界上著名的莱布尼茨三角形如图所示，请编程输出图中排在第n行从左边数第m个位置上的数。

输入
共一行，有二个整数N 和M(N<=15)，两数间用空格隔开。
输出
共一行，有二个整数，两数间用“/”隔开，表示所求的分数，行尾没有多余的空格。
样例输入 Copy
7 3
样例输出 Copy
1/105

思路：
这个题我的思路是先建立起图示的三角形，然后查找就可以了，观察这个三角形，利用我高中对数组求和留下的深刻印象，我一眼就发现了，从第三列开始，每一列从第二个数开始等于它上一行前一列的数减去它前一个数，即a[i][j] = a[i-1][j-1] - a[i][j-1]，同时这个三角形又是对称的，即a[i][j] = a[i][i-j+1]，我们知道分子一定是1，所以每次只需要计算分母就可以了

int a[20][20];
int n,m,ans;
int jianfa(int a,int b)//求分母 
{int x,y,z;z = gcd(a,b);y = a*b/z;x = 1*(y/a)-1*(y/b);z = gcd(x,y);y = y/z;return y;
}int main()
{cin >> n >> m;for(int i=1;i<=15;i++){a[i][1] = a[i][i] = i; }for(int i=3;i<=15;i++){for(int j=2;j<=(i-1)/2+1;j++)//上取整 {a[i][j] = a[i][i-j+1] = jianfa(a[i-1][j-1],a[i][j-1]);}}for(int i=1;i<=15;i++){for(int j=1;j<=15;j++){ans = a[n][m];}}printf("1/%d",ans);return 0;
}

问题 E: 黑匣子

题目描述
Black Box是一种原始的数据库。它可以存储一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的，而i等于0。这个Black Box要处理一串命令。
命令只有两种：
ADD（x）：把x元素放进Black Box；
GET：i加1，然后输出Black Box中第i小的数。
记住：第i小的数，就是Black Box里的数按从小到大的顺序排序后的第i个元素。
例如： 我们来演示一下一个有11个命令的命令串。（如下图所示）
序号 操作 i 数据库 输出
1 ADD(3) 0 3
2 GET 13 3
3 ADD(1) 11, 3
4 GET 21,3 3
5 ADD(-4) 2 -4,1, 3
6 ADD(2) 2-4,1,2,3
7 ADD(8) 2-4,1,2,3,8
8 ADD(-1000)2-1000,-4,1,2,3,8
9 GET 3 -1000,-4,1,2,3,81
10 GET 4 -1000,-4,1,2,3,8 2
11 ADD(2) 4-1000,-4,1,2,2,3,8

现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多有200000个。

现在用两个整数数组来表示命令串：
1、A(1),A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对不超过2000000000的整数，M≤200000。例如上面的例子就是
A=（3,1,-4,2,8,-1000,2）。
2、u(1),u(2),…u(N)：表示第u(j)个元素被放进了Black Box里后就出现了一个GET命令。例如上面的例子中的u=（1,2,6,6）。
输入数据不用判错。

输入
第一行，两个整数，M，N。
第二行，M个整数，表示A(1) …A(M)。
第三行，N个整数，表示u(1)…u(N)。
输出
输出Black Box根据命令串所得出的输出串，一个数字一行。
样例输入 Copy
7 4
3 1 -4 2 8 -1000 2
1 2 6 6
样例输出 Copy
3
3
1
2
提示
对于30%的数据，M≤10000；
对于50%的数据，M≤100000
对于100%的数据，M≤200000

思路：
这个题的题意我是读了好几遍才明白的，它是说有一个堆，一开始是个空堆，同时有一个变量s = 0，现在有两种操作，ADD和GET，ADD表示元素要入队，当当前第u[i]个数入队时，GET一下，s++，并且输出当前第s小的数。由于要不停的输出第s小的数，我想了很久，发现用数组一遍遍的查找太麻烦，于是想到了今天看了很久的数据结构，发现这个规律貌似可以用优先队列来解决
用两个优先队列分别维护a[i]和u[i]，将a[i]存放在大根堆中，如果大根堆的元素数量大于s时，就把大根堆的队顶元素放进小根堆，一旦满足GET的条件，只需要输出当前小根堆的队顶元素即可

int a[maxn],b[maxn],n,m;
int main()
{cin >> n >> m;for(int i=1; i<=n; i++)	scanf("%d",&a[i]);for(int i=1; i<=m; i++)	scanf("%d",&b[i]);int s = 0,k = 1;for(int i=1; i<=n; i++){q2.push(a[i]);//入队 if(q2.size() > s) q1.push(q2.top()),q2.pop();//q2的队顶元素放进q1while(b[k] == i)//遇到这个操作，相对应的迭代器s++ //输出第s小，放进q1的自动按小到大排序，每次输出队顶元素即可 {printf("%d\n",q1.top());k++;//控制循环 s++;q2.push(q1.top());//放回q2 q1.pop(); }}return 0;
}

问题 F: 选地址

题目描述
小X有很多朋友、、分布在N个城市。。
这N个城市之间，有些有直接的道路，有些是间接联通的（保证任何两个城市都可以相互到达。。）
但是、经过每条道路都是有代价的、、
于是。。
小X希望你来帮他找出一个城市，使得他的所有朋友到这个城市的代价最小。
输入
输入共2N+1行，
其中第一行为一个整数N、
第2~N+1行
每行有N个整数、表示两个城市间的代价、（0表示不直接连通）
第n+2~2N+1行
每行一个整数。表示每个城市中小X的朋友数。
输出
输出有两行。
第一行为你选中的城市
第二行为最小需要的代价。
样例输入 Copy
5
0 1 2 0 0
1 0 0 0 20
2 0 0 10 0
0 0 10 0 1
0 20 0 1 0
2
3
4
5
6
样例输出 Copy
4
109
提示
对于100%的数据，n<=200,输出保证不超过long long int

思路：
这个题一开始做的时候，明白题意但是不会啊，基本无从下手，后来得到dalao指点，去学习了弗洛伊德最短路。这个题就是求出每两个城市之间的最短路径，然后去乘以相应的朋友数量，取最小值

int n;
ll ans,tmp,id;
ll dis[1000][1000],num[1000];
// i -> j 的最短路径的长度 
int main()
{int n;	scanf("%d",&n);memset(dis,0x3f3f3f3f,sizeof dis);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){ll x;	scanf("%lld",&x);if(x)//不为0时说明直接连通{dis[i][j] = x;}}}for(int i=1;i<=n;i++)	scanf("%lld",&num[i]);for(int k=1;k<=n;k++)//弗洛伊德最短路 O(n^3){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(dis[i][k] + dis[k][j] < dis[i][j]){dis[i][j] = dis[i][k] + dis[k][j];//求出两个城市之间的最短路径}}}}ans = 1e18 , id = -1;//赋ans一个很大的值for(int i=1;i<=n;i++){tmp = 0;for(int j=1;j<=n;j++){if(i != j)tmp += num[j] * dis[i][j];}if(ans > tmp){ans = tmp;id = i;}}printf("%lld\n%lld\n",id,ans);return 0;
}