本文主要是介绍GCC 优化等级(O0、O1、O2、O3)对程序性能的影响,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 代码示例
- 性能差异
- 探究原因
- 附录
前言
GCC 有 O0、O1、O2、O3 四级优化等级,你知道它们对程序性能有多少影响吗?知道性能差异产生的根本原因是什么吗?今天就和大家一起研究下。
代码示例
combine4.c
#include <stdio.h>#define COUNT 100000000int data[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};void combine4(int *sum)
{int k;int i;*sum = 0;for (k = 0; k < COUNT; k++) {for (i = 0; i < sizeof(data) / sizeof(data[0]); i++) {*sum += data[i];}}
}int main(int argc, char *argv[])
{int sum = 0;combine4(&sum);printf("sum = %d\n", sum);return 0;
}
其中,combine4() 是个累加求和的函数,它就是我们今天研究性能的主角。
性能差异
先直观感受下不同优化等级对应的性能差异
O0
$ gcc books/csapp/combine4.c -o books/csapp/combine4.out -Wall -g -O0
$ time books/csapp/combine4.out
sum = 205032704real 0m1.975s
user 0m1.968s
sys 0m0.007s
O1
$ gcc books/csapp/combine4.c -o books/csapp/combine4.out -Wall -g -O1
$ time books/csapp/combine4.out
sum = 205032704real 0m0.345s
user 0m0.345s
sys 0m0.000s
O2
$ gcc books/csapp/combine4.c -o books/csapp/combine4.out -Wall -g -O2
$ time books/csapp/combine4.out
sum = 205032704real 0m0.384s
user 0m0.382s
sys 0m0.001s
O3
$ gcc books/csapp/combine4.c -o books/csapp/combine4.out -Wall -g -O3
$ time books/csapp/combine4.out
sum = 205032704real 0m0.002s
user 0m0.001s
sys 0m0.001s
| 优化等级 | 执行耗时 | 速度提升 |
|---|---|---|
| O0 | 1.975s | 1 倍 |
| O1 | 0.345s | 5 倍 |
| O2 | 0.384s | 5 倍 |
| O3 | 0.002s | 987 倍 |
可以看到,以 O0 为基准,O1 和 O2 速度提升了 5 倍,O3 提升了令人难以置信的 987 倍。
探究原因
要想弄清楚速度提升的原因,最好的办法就是看程序对应的汇编代码。
有看不懂汇编的小伙伴,可以去看文章最后的附录,我对每行汇编代码都作了注释。
O0

O1
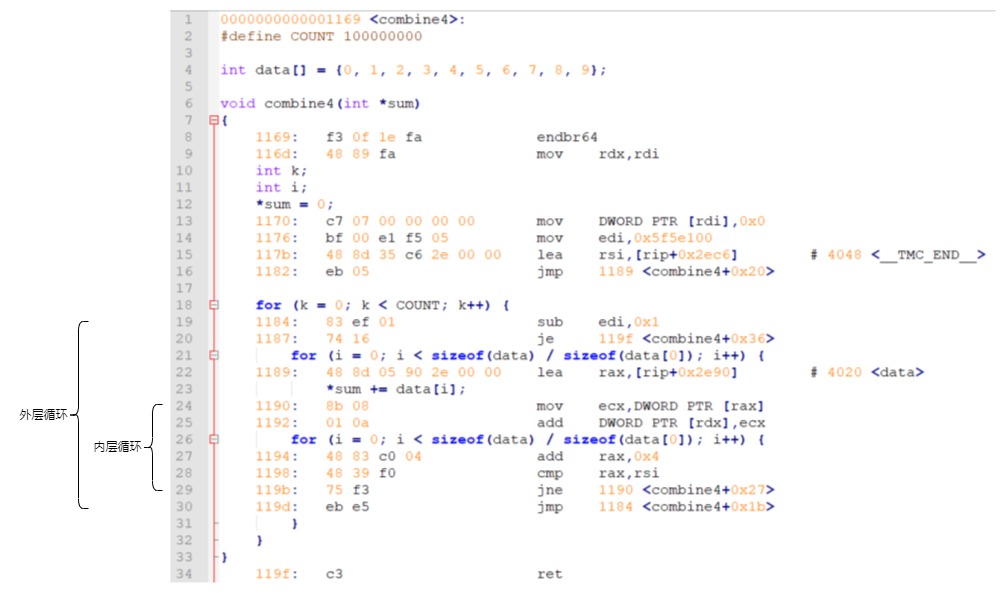
从 O0 到 O1,一个明显的变化就是指令数量变少了,从 51 行缩减为 34 行,并且这是循环部分的指令,减少的行数要乘以循环次数,单从这方面,就可知能够缩短相当可观的运行时间。(其中一点:O0 使用 eax 来存储计算结果,并在每次计算结束后将结果刷入内存 [rbp-0x18](对应第 33~35 行),而 O1 直接将计算的结果存入内存 [rdx](对应第 25 行)。指令从三行变为一行,速度提升。)
另一个变化是,使用寄存器 rsi 存储 data 数组的末尾地址(对应第 15 行汇编代码),使用 rax 存储数组偏移,内层循环的边界判断条件直接使用这两个寄存器进行比较。这种方式省略了变量 i,变量 i 是存储在内存中的,对内存进行取值、自增计算、重新写入内存,要比寄存器操作慢得多,所以这也是提升运行速度的一个重要因素。
另一个变化是,存储 data 数组的末尾地址(对应第 15 行汇编代码),使用该地址作为内层循环边界判断的条件,这样就可以省略 i 变量,省略 i 变量占用寄存器的开销。别小看一个寄存器的开销,要知道常用寄存器的数量总共才十几个,少一个变量的存储,就少了一个寄存器倒腾的开销,效率就会大幅提高。想象一下,有两个杯子,分别装有两种不同颜色的水,让你交换两个杯子中的水,这时候如果能给你一个空杯子倒腾一下,问题就很好解决,否则,甚至无法解决。从这个故事中体会一下一个寄存器能够产生的性能影响程度。
(O2 和 O1 性能差不多,就不进行分析了。)
O3
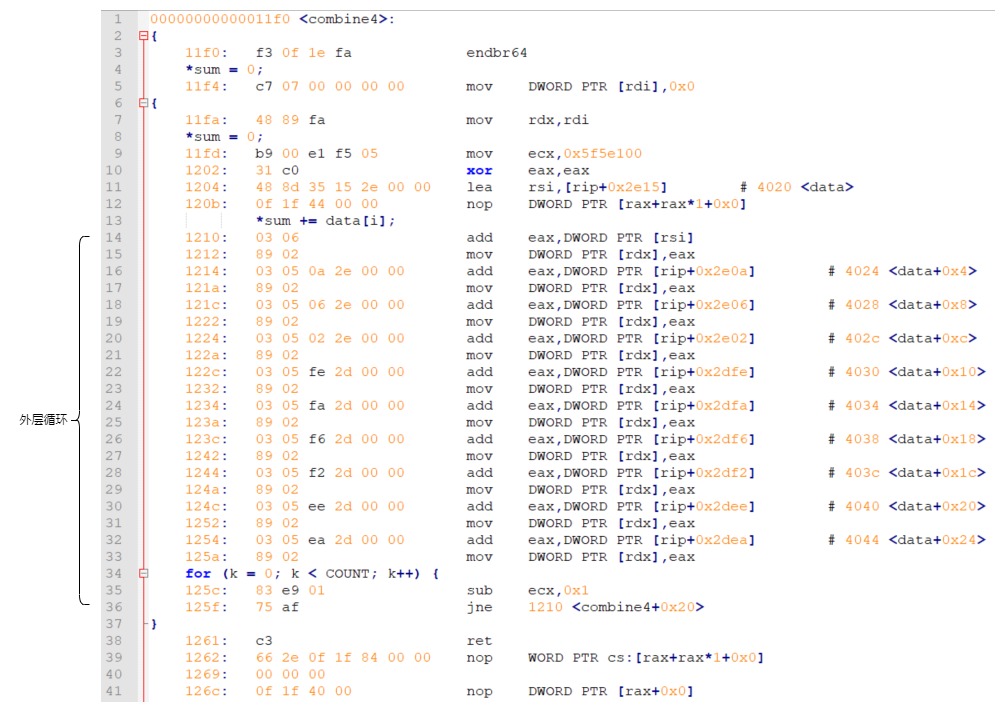
O3 直接将内层循环给优化掉了,10 次循环展开成 10 次指令,也是牛逼。
这样一来,少了内层循环的边界判断。更重要的是,少一层跳转,就减少一次分支预测判断,这对指令执行的效率有显著提升。
附录
O0
0000000000001169 <combine4>:
# 在间接跳转之后查看下一条指令是不是endbr64。如果指令是endbr64指令,那么该指令会将CPU状态从WAIT_FOR_ENDBRANCH恢复成DLE。另一方面,如果下一条指令不是endbr64,说明程序可能被控制流劫持了,CPU就报错(#CP)。因为按照正确的逻辑,间接跳转后应该需要有一条对应的endbr64指令来回应间接跳转,如果不是endbr64指令,那么程序控制流可能被劫持并前往其它地址(其它任意地址上是以非endbr64开始的汇编代码)(涉及编译器兼容CPU新特性)。——https://blog.csdn.net/clh14281055/article/details/1174465881169: f3 0f 1e fa endbr64
# 将rbp数值压入栈中,可分解为:
# rsp = rsp - 8
# rsp = rbp
# https://www.cnblogs.com/tongongV/p/13713210.html116d: 55 push rbp
# rbp = rsp116e: 48 89 e5 mov rbp,rsp
# [rbp - 0x18] = rdi
# 关于64位汇编的参数传递
# 当参数少于等于 6 个时, 参数从左到右放入寄存器: rdi, rsi, rdx, rcx, r8, r9。
# 当参数为7个及以上时, 前 6 个与前面一样, 但后面的依次从 “右向左” 放入栈中,
# —— https://www.cnblogs.com/volva/p/11814998.html1171: 48 89 7d e8 mov QWORD PTR [rbp-0x18],rdi
# rax = [rbp - 0x18]
# 结合上文,推导出 rax = rdi1175: 48 8b 45 e8 mov rax,QWORD PTR [rbp-0x18]
# [rax] = 0
# 结合上文,推导出 *rdi = 0
# 对应 C 代码 *sum = 0;1179: c7 00 00 00 00 00 mov DWORD PTR [rax],0x0
# [rbp - 0x8] = 0
# 对应 C 代码 k = 0;117f: c7 45 f8 00 00 00 00 mov DWORD PTR [rbp-0x8],0x0
# 跳转到 0x11c6
# jmp 无条件跳转指令1186: eb 3e jmp 11c6 <combine4+0x5d>
# [rbp - 0x4] = 0
# 对应 C 代码 i = 0;1188: c7 45 fc 00 00 00 00 mov DWORD PTR [rbp-0x4],0x0
# 跳转到 0x11ba118f: eb 29 jmp 11ba <combine4+0x51>
# rax = [rbp - 0x18]
# rax = sum1191: 48 8b 45 e8 mov rax,QWORD PTR [rbp-0x18]
# edx = rax
# edx = sum1195: 8b 10 mov edx,DWORD PTR [rax]
# eax = [rbp - 0x4]
# eax = i1197: 8b 45 fc mov eax,DWORD PTR [rbp-0x4]
# cdqe使用eax的最高位拓展rax高32位的所有位
# rax = eax
# rax = i119a: 48 98 cdqe
# rcx = i * 4119c: 48 8d 0c 85 00 00 00 lea rcx,[rax*4+0x0]11a3: 00
# rax = data11a4: 48 8d 05 75 2e 00 00 lea rax,[rip+0x2e75] # 4020 <data>
# eax = rcx + rax
# eax = i * 4 + data
# eax = data[i]11ab: 8b 04 01 mov eax,DWORD PTR [rcx+rax*1]
# edx = edx + eax
# sum = sum + data[i]11ae: 01 c2 add edx,eax
# rax = sum11b0: 48 8b 45 e8 mov rax,QWORD PTR [rbp-0x18]
# sum = sum11b4: 89 10 mov DWORD PTR [rax],edx
# i++11b6: 83 45 fc 01 add DWORD PTR [rbp-0x4],0x1
# eax = [rbp - 0x4]
# 即 eax = i;11ba: 8b 45 fc mov eax,DWORD PTR [rbp-0x4]
# eax 和 0x9 比较
# 对应 C 代码 i < 10;11bd: 83 f8 09 cmp eax,0x9
# 无符号小于或等于,跳转到 0x119111c0: 76 cf jbe 1191 <combine4+0x28>11c2: 83 45 f8 01 add DWORD PTR [rbp-0x8],0x1
# [rbp - 0x8] 和 99,999,999 比较
# 对应 C 代码 k < 10000000011c6: 81 7d f8 ff e0 f5 05 cmp DWORD PTR [rbp-0x8],0x5f5e0ff
# 如果小于或等于,跳转到 0x1188
# 汇编指令注解:Jump if less or equal
# —— https://blog.csdn.net/jiarong66/article/details/4435039511cd: 7e b9 jle 1188 <combine4+0x1f>11cf: 90 nop11d0: 90 nop
# 将栈顶数据弹出到 rbp, 可以分解为:
# rbp = rsp
# rsp = rsp - 811d1: 5d pop rbp
# 返回11d2: c3 ret
O1
0000000000001169 <combine4>:1169: f3 0f 1e fa endbr64
# rdx = sum116d: 48 89 fa mov rdx,rdi
# sum = 0;1170: c7 07 00 00 00 00 mov DWORD PTR [rdi],0x0
# edi = 100,000,0001176: bf 00 e1 f5 05 mov edi,0x5f5e100
# data 数组的末尾117b: 48 8d 35 c6 2e 00 00 lea rsi,[rip+0x2ec6] # 4048 <__TMC_END__>
# 跳转到 0x11891182: eb 05 jmp 1189 <combine4+0x20>
# edi = edi - 1;1184: 83 ef 01 sub edi,0x1
# edi - 1 < 0 时, 跳转到 0x119f ?1187: 74 16 je 119f <combine4+0x36>
# rax = data1189: 48 8d 05 90 2e 00 00 lea rax,[rip+0x2e90] # 4020 <data>
# ecx = data1190: 8b 08 mov ecx,DWORD PTR [rax]
# sum = sum + data1192: 01 0a add DWORD PTR [rdx],ecx
# data++1194: 48 83 c0 04 add rax,0x4
# data 是否到达了数组末尾1198: 48 39 f0 cmp rax,rsi
# 没有的话跳转到 0x1190 // 内层循环119b: 75 f3 jne 1190 <combine4+0x27>
# 跳转到 0x1184 // 外层循环119d: eb e5 jmp 1184 <combine4+0x1b>
# 函数返回119f: c3 ret
O3
00000000000011f0 <combine4>:11f0: f3 0f 1e fa endbr64
# sum = 011f4: c7 07 00 00 00 00 mov DWORD PTR [rdi],0x0
# rdx = sum11fa: 48 89 fa mov rdx,rdi
# ecx = 100,000,00011fd: b9 00 e1 f5 05 mov ecx,0x5f5e100
# eax = eax 异或 eax
# 是异或运算,两数相反为1;两数相同为0。由于这两个数相同,异或后等于清0
# 由于它比mov eax,0效率高,所以一般用它!
# eax = 01202: 31 c0 xor eax,eax
# rsi = data1204: 48 8d 35 15 2e 00 00 lea rsi,[rip+0x2e15] # 4020 <data>
# 120b: 0f 1f 44 00 00 nop DWORD PTR [rax+rax*1+0x0]
# eax = eax + data1210: 03 06 add eax,DWORD PTR [rsi]
# sum = eax1212: 89 02 mov DWORD PTR [rdx],eax
# eax = data + 0x4
# eax = eax + data[1]1214: 03 05 0a 2e 00 00 add eax,DWORD PTR [rip+0x2e0a] # 4024 <data+0x4>
# sum = eax121a: 89 02 mov DWORD PTR [rdx],eax
# eax = eax + data[2]121c: 03 05 06 2e 00 00 add eax,DWORD PTR [rip+0x2e06] # 4028 <data+0x8>1222: 89 02 mov DWORD PTR [rdx],eax1224: 03 05 02 2e 00 00 add eax,DWORD PTR [rip+0x2e02] # 402c <data+0xc>122a: 89 02 mov DWORD PTR [rdx],eax122c: 03 05 fe 2d 00 00 add eax,DWORD PTR [rip+0x2dfe] # 4030 <data+0x10>1232: 89 02 mov DWORD PTR [rdx],eax1234: 03 05 fa 2d 00 00 add eax,DWORD PTR [rip+0x2dfa] # 4034 <data+0x14>123a: 89 02 mov DWORD PTR [rdx],eax123c: 03 05 f6 2d 00 00 add eax,DWORD PTR [rip+0x2df6] # 4038 <data+0x18>1242: 89 02 mov DWORD PTR [rdx],eax1244: 03 05 f2 2d 00 00 add eax,DWORD PTR [rip+0x2df2] # 403c <data+0x1c>124a: 89 02 mov DWORD PTR [rdx],eax124c: 03 05 ee 2d 00 00 add eax,DWORD PTR [rip+0x2dee] # 4040 <data+0x20>1252: 89 02 mov DWORD PTR [rdx],eax1254: 03 05 ea 2d 00 00 add eax,DWORD PTR [rip+0x2dea] # 4044 <data+0x24>125a: 89 02 mov DWORD PTR [rdx],eax125c: 83 e9 01 sub ecx,0x1125f: 75 af jne 1210 <combine4+0x20>1261: c3 ret 1262: 66 66 2e 0f 1f 84 00 data16 nop WORD PTR cs:[rax+rax*1+0x0]1269: 00 00 00 00 126d: 0f 1f 00 nop DWORD PTR [rax]这篇关于GCC 优化等级(O0、O1、O2、O3)对程序性能的影响的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




