HDU-2571 命运 广度优先搜索BFS+动态规划DP 题解

Problem Description

穿过幽谷意味着离大魔王lemon已经无限接近了！
可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！
可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！
命运大迷宫可以看成是一个两维的方格阵列，如下图所示：

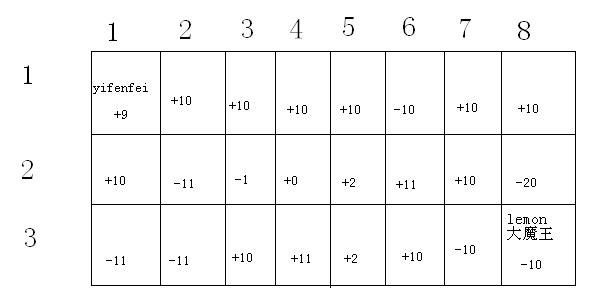
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。
为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

Input

输入数据首先是一个整数C，表示测试数据的组数。
每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)；
接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。

Output

请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。

Sample Input

1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10

Sample Output

52

题目分析

请耐心看到底~本题就一道DP水题，不要被吓住

那张**图太瘆人了，会影响你做题的，就不放上来了~

首先，如果你认为这道题是搜索，那么也无伤大雅，因为他还真是搜索

但不是DFS，因为也是在图中根据代价找路径，但是：这不是迷宫，你可以选择任何一条对答案有正贡献的路径，那么深搜绝对不是这道题的优选解决方案

那考虑一下BFS吧，我们从左上角出发，根据题目描述，我们一共有三种移动方式，我们走到一个点时，先将三种走法全部入队，同时用一个二维图记录每个坐标点的幸运值，在维护队列时，以后的坐标只有在大于先前坐标点的幸运值的时候，才允许该点入队，我们实现一下

#include <bits/stdc++.h>
using namespace std;
const int N = 30, M = 1100;
int g[N][M], max1, ans, n, m, val[N][M];typedef struct node{int x, y, w;}node;
queue<node> q;void bfs(){struct node head, tail, now;int x, y, i, j, d;head.x = head.y = 1;head.w = g[1][1];q.push(head);while (!q.empty()){head = q.front();q.pop();if (head.x == n && head.y == m){if (head.w > max1) max1 = head.w;}now.x = head.x + 1;now.y = head.y;now.w = head.w + g[now.x][now.y];if (now.x >= 1 && now.y >= 1 && now.x <= n && now.y <= m && val[now.x][now.y] < now.w){val[now.x][now.y] = now.w;q.push(now);}now.x = head.x;now.y = head.y + 1;now.w = head.w + g[now.x][now.y];if (now.x >= 1 && now.y >= 1 && now.x <= n && now.y <= m && val[now.x][now.y] < now.w){val[now.x][now.y] = now.w;q.push(now);}now.x = head.x;for (d = 2; d <= m; d++){now.y = head.y * d;if (now.y > m) break;now.w = head.w + g[now.x][now.y];if (now.x >= 1 && now.y >= 1 && now.x <= n && now.y <= m && val[now.x][now.y] < now.w){val[now.x][now.y] = now.w;q.push(now);}}}return;
}int main(){int t, i, j; cin >> t;while (t--){cin >> n >> m;memset(val, 0, sizeof(val));for (i = 1; i <= n; i++)for (j = 1; j <= m; j++) cin >> g[i][j];max1 = INT_MIN;bfs();cout << max1 << endl;}return 0;
}

？？？WTF，，，这么长，这么麻烦？？？思路可能不大对…我们还是再分析分析题吧~

这个玄学的人要取得最大的幸运值，还要从左上角走到右下角，我们读入幸运值的时候，可能会感觉到一丝熟悉感：这，莫非是DP？

这次猜对了。下面分析一下DP的思路：一共有三种走法：横着走、竖着走、跳着走。那么我们用$dp[i][j]$表示坐标为走到$(i,j)$处的最大幸运值，那么我们可以推导出状态转移方程：

• 横着走：$dp[i][j+1]=max(dp[i][j+1],dp[i][j]+g[i][j+1])$
• 竖着走：$dp[i+1][j]=max(dp[i+1][j],dp[i][j]+g[i+1][j])$
• 跳着走：$dp[i][j\ast k]=max(dp[i][j\ast k],dp[i][j]+g[i][j\ast k])$

以横着走为例，我们来分析一下状态转移方程是如何推导出来的:

不妨设当前位置的坐标$(i,j+1)$，假设我们通过上述三种方式都能够到达这个点：

无论是那种方式，如果是第一次到达，那么幸运值应该立即被记录下来，由于数组初始化为0了，取一下MAX自然就更新了

如果是第n次到达，由于我们是乱序访问的，因此访问到再次访问这个点的时候，需要将本次访问带来的新值与历史的记录值进行比较，留下较大的值，这便是$max(dp[i][j+1],dp[i][j]+g[i][j+1])$的含义

一道水题分析这么多，，，不大合适。上DP代码吧

#include <bits/stdc++.h>
using namespace std;
int g[30][10010];
int dp[30][10010];int main(){int c = 0; cin >> c;while(c--){int n, m; cin >> n >> m;memset(g, 0, sizeof(g));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> g[i][j];dp[i][j] = INT_MIN;} }dp[1][1] = g[1][1];for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(i + 1 <= n) dp[i + 1][j] = max(dp[i + 1][j], dp[i][j] + g[i + 1][j]);if(j + 1 <= m) dp[i][j + 1] = max(dp[i][j + 1], dp[i][j] + g[i][j + 1]);for(int k = 2; k <= m / j; k++) dp[i][j * k] = max(dp[i][j * k], dp[i][j] + g[i][j * k]);}}cout << dp[n][m] << endl;}return 0;
}

2; k <= m / j; k++) dp[i][j * k] = max(dp[i][j * k], dp[i][j] + g[i][j * k]);
}
}
cout << dp[n][m] << endl;
}
return 0;
}