管道铺设系统-最小生成树（Prim、Kruskal算法实现）

2023-10-22 09:59
文章标签 算法 实现 系统 最小 生成 管道 prim kruskal 铺设

本文主要是介绍管道铺设系统-最小生成树（Prim、Kruskal算法实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

管道铺设系统-最小生成树（Prim、Kruskal算法实现）

问题

开发一个管线铺设辅助系统，以我校东校区为例，在东校区大学生活动中心、学生公寓、学生食堂、21层主楼、第一、二、三、四教学楼、原图书馆、机械馆、原信息馆、人文馆、体育馆之间铺设输水管道，设计算法并实现使铺设的输水管道距离最短。系统要求具备从文本读取数据、显示最佳铺设方案，以及绘制最佳方案的简单示意图等功能。

功能需求

1）将管线经过的建筑物以及建筑物之间的距离，抽象成无向图，并以矩阵的形式表示，并保存在文本中，系统通过读取文本的方式，获取该矩阵;
2）从Prim算法和Kruskal算法中至少选择一种实现管线铺设的最优方案，系统可以最优方案的生成过程，并且可以文本的形式输出;
3)在系统上可以生成最优方案的简易图。

功能实现

Prim算法
（1）基本思想：
设N=(V,E)是最小连通网，TE是N上最小生成树中边的集合，初始令U={u0}（u0∈V),TE={}。
在所有u∈U,v∈V-U的边（u，v）∈E中，找一条代价最小的边（u0,v0),将边（u0,v0）并入集合TE，同时v0并入U。
重复上述操作，直到U=V为止，则T=(V,TE)为N的最小生成树。
（2）代码展示：
①定义顶点数据类型。由于我们需要绘制出最小生成树的动态过程，所以需要记录顶点的坐标。顶点数据类型为我们定义的结构体类型，它包括三个信息，即x坐标，y坐标和顶点名称。

//点 
typedef struct
{char data;int x;int y;
}VerTex;

②定义图的信息。图的信息包括点集、邻接矩阵、点的个数和边的个数。

typedef struct
{VerTex vexs[MVNum];int arcs[MVNum][MVNum];int vexnum, arcnum;
}AMGraph;

③定义候选最短边集数组closeEdge[n],数组元素包括 adjvex 和 lowcost两个域，分别表示候选最短边的邻接点和权值。

// 定义记录从顶点集U到V-U代价最小的边的数组
typedef struct {char adjvex; // 候选最短边邻接点 int lowcost; // 候选最短边权值 
}arr;
arr closedge[MVNum];

(3)运行结果
①选择Prim起点，生成最小生成树
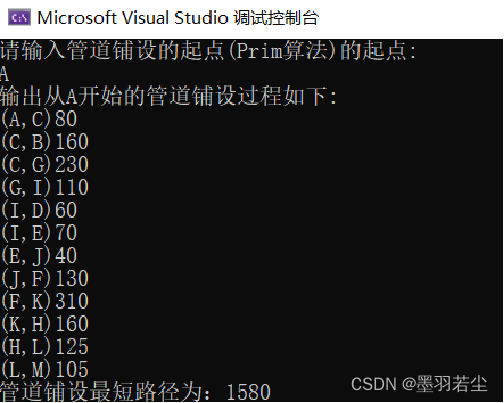
在这里插入图片描述
②动态过程展示
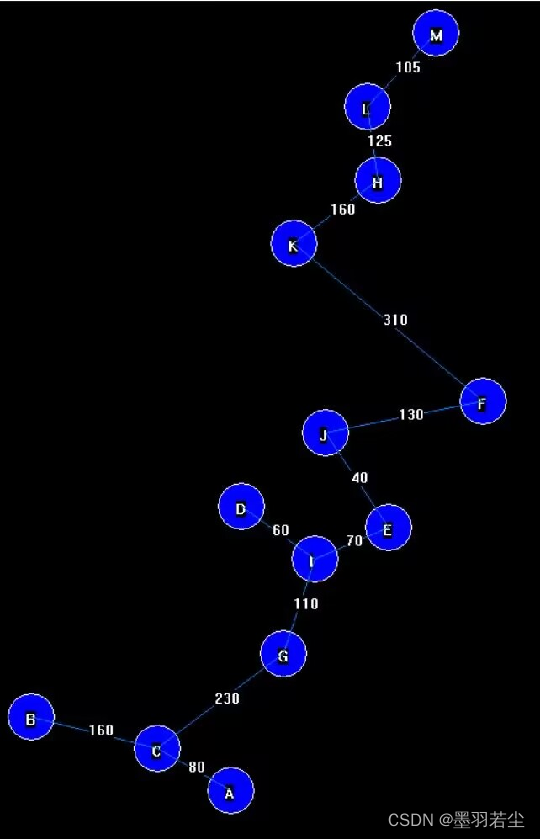
在这里插入图片描述
③保存在文本文档中
在这里插入图片描述
Kruska算法
(1)运行结果
①依次按下回车键，构建最小生成树
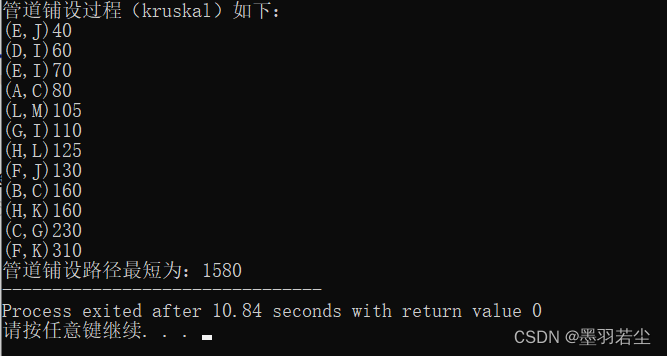
在这里插入图片描述
②动态过程展示
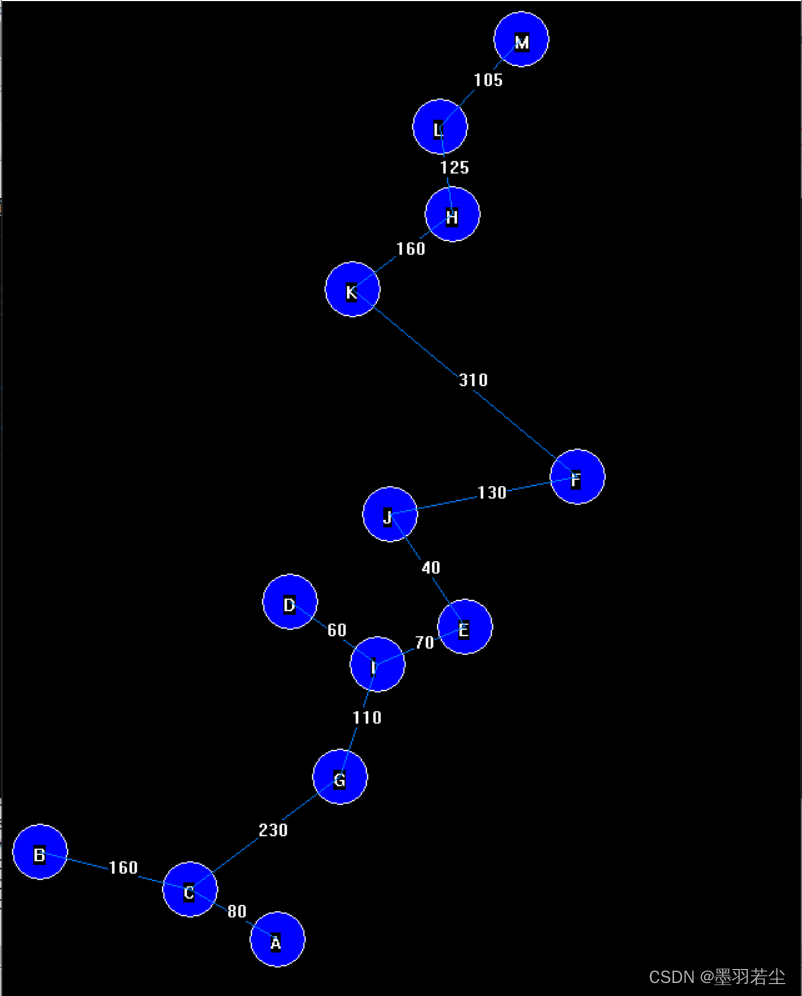
在这里插入图片描述

③保存在文本文档中
在这里插入图片描述

参考资料

[1] https://www.bilibili.com/video/BV1yp4y1Q74o?share_source=copy_web
[2] http://t.csdn.cn/4jtnv
[3] http://t.csdn.cn/qXRBx
[4]https://jingyan.baidu.com/article/b2c186c8c86d7c856ef6fffd.html

附：
读取的文本：

13 78
A 220 750
B 30 680
C 150 710
D 230 480
E 370 500
F 460 380
G 270 620
H 360 170
I 300 530
J 310 410
K 280 230
L 350 100
M 415 30
0 255 80 380 410 550 260 865 350 440 775 980 1100
255 0 160 370 450 590 310 840 380 470 730 930 1000
80 160 0 330 380 530 230 820 320 410 720 920 1000
380 370 330 0 100 230 130 490 60 110 390 580 680
410 450 380 100 0 150 150 470 70 40 380 560 650
550 590 530 230 150 0 300 350 220 130 310 450 530
260 310 230 130 150 300 0 610 110 185 550 715 810
865 840 820 490 470 350 610 0 500 420 160 125 210
350 380 320 60 70 220 110 500 0 80 440 600 705
440 470 410 110 40 130 185 420 80 0 370 525 625
775 730 720 390 380 310 550 160 440 370 0 190 300
980 930 920 580 560 450 715 125 600 525 190 0 105
1100 1000 1000 680 650 530 810 210 705 625 300 105 0

程序源码：
（1）Prim

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include<graphics.h> 
#include<conio.h>
#include<wchar.h>
#include<fstream>
using namespace std;
#define MaxInt 32767
#define MVNum 100
int sum = 0;//点 
typedef struct
{char data;int x;int y;
}VerTex;typedef struct
{VerTex vexs[MVNum];int arcs[MVNum][MVNum];int vexnum, arcnum;
}AMGraph;// 定义记录从顶点集U到V-U代价最小的边的数组
typedef struct {char adjvex; // 候选最短边邻接点 int lowcost; // 候选最短边权值 
}arr;
arr closedge[MVNum];//确定顶点在G中的位置
int LocateVex(AMGraph G, char v)
{for (int i = 0; i < G.vexnum; ++i){if (G.vexs[i].data == v){return i;}}return -1;
}
//采用邻接矩阵表示法，创建无向网G
//int CreateUDN(AMGraph& G)
//{
//    int w;
//    char v1, v2;
//    //for (int i = 0; i < G.vexnum; ++i)
//    //    for (int j = 0; j < G.vexnum; ++j)
//    //    {
//    //        G.arcs[i][j] = MaxInt;
//    //    }
//    //ReadFromTxt(G);
//    //for (int k = 0; k < G.arcnum; ++k)
//    //{
//    //    int i, j;
//    //    cout << "请输入第" << k + 1 << "条边依附的顶点及权值：";
//    //    cin >> v1 >> v2 >> w;
//    //    i = LocateVex(G, v1);
//    //    j = LocateVex(G, v2);
//    //    G.arcs[i][j] = w;
//    //    G.arcs[j][i] = G.arcs[i][j];
//    //}
//    return 1;
//}//从txt文件中读取邻接矩阵
void ReadFromTxt(AMGraph& G) {ifstream fin;fin.open("E:\\distance.txt", ios::in);if (!fin.is_open()) {cout << "文件打开失败" << endl;exit(1);}while (!fin.eof()) {fin >> G.vexnum >> G.arcnum;for (int i = 0; i < G.vexnum; i++) {fin >> G.vexs[i].data >> G.vexs[i].x >> G.vexs[i].y;}for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {fin >> G.arcs[i][j];}}fin.close();}
}void SaveToTxt(char A, int B, char p) {ofstream fout("result_prim.txt",ofstream::app);if (fout.is_open()) {fout << "(" << A << "," << p << ")" << B << endl;}fout.close();
}void MinSpanTree_PRIM(AMGraph G, char u) {// 用普里姆算法从第u个顶点出发构造网G的最小生成树T，输出T的各条边int k;k = LocateVex(G, u);//画点 setfillcolor(RGB(0, 0, 255));int radio = 22; // 圆的半径 fillcircle(G.vexs[k].x, G.vexs[k].y, radio);outtextxy(G.vexs[k].x - 5, G.vexs[k].y - 5, G.vexs[k].data);_getch();// 初始化辅助数组for (int j = 0; j < G.vexnum; ++j){closedge[j].lowcost = G.arcs[k][j];closedge[j].adjvex = u;}closedge[k].lowcost = 0;  //初始，U={u}int x1, x2, y1, y2;//画点线 int m;for (int i = 1; i < G.vexnum; ++i){// 寻找最短边的邻接点int min = MaxInt;for (int n = 0; n < G.vexnum; ++n){if (closedge[n].lowcost < min && closedge[n].lowcost != 0){min = closedge[n].lowcost;k = n;}}//画点 setfillcolor(RGB(0, 0, 255));int radio = 22; // 圆的半径 fillcircle(G.vexs[k].x, G.vexs[k].y, radio);outtextxy(G.vexs[k].x - 5, G.vexs[k].y - 5, G.vexs[k].data);_getch();char p;p = G.vexs[k].data;// 输出最小生成树路径cout << "(" << closedge[k].adjvex << "," << p << ")" << closedge[k].lowcost << endl;//char A = closedge[k].adjvex;//int B = closedge[k].lowcost;SaveToTxt(closedge[k].adjvex, closedge[k].lowcost, p);sum = sum + closedge[k].lowcost;m = LocateVex(G, closedge[k].adjvex);x1 = G.vexs[m].x;y1 = G.vexs[m].y;x2 = G.vexs[k].x;y2 = G.vexs[k].y;// cout << p << endl;char str[100];line(x1, y1, x2, y2);sprintf(str, "%d", closedge[k].lowcost); //转换成字符outtextxy((x1 + x2 - 10) / 2, (y1 + y2 - 20) / 2, str); //放权值 _getch();//第k顶点并入U集closedge[k].lowcost = 0;// 调整数组closedgefor (int j = 0; j < G.vexnum; ++j){if (G.arcs[k][j] < closedge[j].lowcost){closedge[j].lowcost = G.arcs[k][j];closedge[j].adjvex = p;}}}
}int main()
{initgraph(757, 881, SHOWCONSOLE);int i, j;char p;AMGraph G;ReadFromTxt(G);
//    CreateUDN(G);
//    for (int i = 0; i < G.vexnum; i++) {
//        cout << G.vexs[i].data << endl;
//    }
//    for (i = 0; i < G.vexnum; ++i)
//    {
//        for (j = 0; j < G.vexnum; ++j)
//        {
//            if (G.arcs[i][j] != MaxInt)
//                cout << G.arcs[i][j] << "\t";
//            else
//                cout << "0" << "\t";
//        }
//        cout << endl;
//    }
//    cout << endl;cout << "请输入管道铺设的起点(Prim算法)的起点:" << endl;cin >> p;cout << "输出从" << p << "开始的管道铺设过程如下:" << endl;MinSpanTree_PRIM(G, p);cout<<"管道铺设最短路径为："<<sum; system("pause");closegraph();return 0;
}

(2) Kruskal

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<string>
#include<graphics.h> 
#include<conio.h>
#include<wchar.h>
#include<fstream>
using namespace std;
#define MVNum 100
int sum = 0; //记录最小生成树总权值 
//边
typedef struct edge_set {char vex1; //边的其中一个顶点char vex2; //边的另一个顶点int weight; //边的权重
}Edge;//点 
typedef struct
{char data;int x;int y;
}VerTex;typedef struct
{VerTex vexs[MVNum];Edge edge[MVNum];int arcs[MVNum][MVNum];int vexnum, arcnum;
}Graph;//确定顶点在G中的位置
int locate_vex(Graph G, char v)
{for (int i = 0; i < G.vexnum; ++i){if (G.vexs[i].data == v){return i;}}return -1;
}//从txt文件中读取邻接矩阵
void ReadFromTxt(Graph& G) {ifstream fin;fin.open("E:\\distance.txt", ios::in);if (!fin.is_open()) {cout << "文件打开失败" << endl;exit(1);}int k=0;while (!fin.eof()) {fin >> G.vexnum >> G.arcnum;for (int i = 0; i < G.vexnum; i++) {fin >> G.vexs[i].data >> G.vexs[i].x >> G.vexs[i].y;}//for (int i = 0; i < 13; i++) {//	for (int j = i+1; j < 13; j++) {//		char a = G.vexs[i].data;//		char b = G.vexs[j].data;//		G.edge[k].vex1 = a;//		G.edge[k].vex2 = b;//		fin >> G.edge[k].weight;//		cout<< G.edge[k].weight<<endl;//		k++;//	}//}for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {fin >> G.arcs[i][j];}}fin.close();}
}void SaveToTxt(char A, int B, char p) {ofstream fout("result_kruskal.txt", ofstream::app);if (fout.is_open()) {fout << "(" << A << "," << p << ")" << B << endl;}fout.close();
}//创建一个图，图的信息使用边集来存储
int create_graph(Graph& G) {//cout << "请输入图的总顶点数及边数：" << endl;//cin >> G.vexnum >> G.arcnum;//cout << "请依次输入各顶点的信息：" << endl;int k = 0;for (int i = 0; i < G.vexnum; i++) {for (int j = i+1; j < G.vexnum; j++) {char a = G.vexs[i].data;char b = G.vexs[j].data;G.edge[k].vex1 = a;G.edge[k].vex2 = b;G.edge[k].weight = G.arcs[i][j];k++;}}//  画点 setfillcolor(RGB(0, 0, 255));int radio = 22;for (int i = 0; i < G.vexnum; ++i){//cout << "请输入第" << i + 1 << "个顶点：";//cin >> G.vexs[i].data;//cout << "请输入第" << i + 1 << "个顶点的x坐标：";//cin >> G.vexs[i].x;//cout << "请输入第" << i + 1 << "个顶点的y坐标：";//cin >> G.vexs[i].y;fillcircle(G.vexs[i].x, G.vexs[i].y, radio);outtextxy(G.vexs[i].x - 5, G.vexs[i].y - 5, G.vexs[i].data);}//cout << "请输入各条边依附的顶点及权值：" << endl;//for (int k = 0; k < G.arcnum; ++k)//{//	int i, j;//	cout << "请输入第" << k + 1 << "条边依附的顶点及权值：";//	cin >> G.edge[k].vex1 >> G.edge[k].vex2 >> G.edge[k].weight;//}return 1;
}//排序，按权重从小到大顺序排
int cmp(const void* a, const void* b) {return ((Edge*)a)->weight - ((Edge*)b)->weight;
}//找树的根
int find_root(int* parent, int t) {while (parent[t] > -1){t = parent[t]; //求顶点t上的双亲直到根结点 }return t;
}//kruskal算法实现
void kruskal(Graph G) {//将边按从小到大顺序排序qsort(G.edge, G.arcnum, sizeof(Edge), cmp);int parent[MVNum]; //判断新添加的线是否能和原来的图构成回路 // 初始化parent数组 for (int i = 0; i < G.vexnum; i++) {parent[i] = -1;}int num = 0, vex1 = -1, vex2 = -1;int p, q;int x1, y1, x2, y2;setlinecolor(RGB(0, 125, 255));for (int i = 0; i < G.arcnum; i++){// cout << G.edge[i].weight << endl;p = locate_vex(G, G.edge[i].vex1);q = locate_vex(G, G.edge[i].vex2);vex1 = find_root(parent, p);vex2 = find_root(parent, q);//cout << vex1 << endl;//cout << vex2 << endl;if (vex1 != vex2) //说明没在同一个连通分量中 {_getch();cout << "(" << G.edge[i].vex1 << "," << G.edge[i].vex2 << ")" << G.edge[i].weight << endl;SaveToTxt(G.edge[i].vex1,G.edge[i].weight,G.edge[i].vex2);sum = sum + G.edge[i].weight;parent[vex2] = vex1;//合并生成树 // 连线 x1 = G.vexs[p].x;y1 = G.vexs[p].y;x2 = G.vexs[q].x;y2 = G.vexs[q].y;char str[100];line(x1, y1, x2, y2);sprintf(str, "%d", G.edge[i].weight); //转换成字符outtextxy((x1 + x2 - 10) / 2, (y1 + y2 - 20) / 2, str); //放权值 num++;}if (num == G.vexnum - 1){Sleep(10000);return;}}
}int main() {initgraph(640, 1280, SHOWCONSOLE);Graph G;ReadFromTxt(G);create_graph(G);//for (int i = 0; i < 13; i++) {//	for (int j = 0; j < 13; j++) {//		cout << G.arcs[i][j];//		cout << " ";//	}//	cout << endl;//}
//	for (int i = 0; i < G.arcnum; i++) {
//		cout <<G.edge[i].vex1 << G.edge[i].vex2 << G.edge[i].weight<< endl;
//	}cout<<"管道铺设过程（kruskal）如下："<<endl;kruskal(G);cout<<"管道铺设路径最短为："<<sum;closegraph();return 0;
}

这篇关于管道铺设系统-最小生成树（Prim、Kruskal算法实现）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/260705。

相关文章

C# string转unicode字符的实现

C# string转unicode字符的实现

《C#string转unicode字符的实现》本文主要介绍了C#string转unicode字符的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随... 目录1. 获取字符串中每个字符的 Unicode 值示例代码：输出：2. 将 Unicode 值格式化
阅读更多...
python安装whl包并解决依赖关系的实现

python安装whl包并解决依赖关系的实现

《python安装whl包并解决依赖关系的实现》本文主要介绍了python安装whl包并解决依赖关系的实现,文中通过图文示例介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面... 目录一、什么是whl文件？二、我们为什么需要使用whl文件来安装python库？三、我们应该去哪儿下
阅读更多...
Python脚本实现图片文件批量命名

Python脚本实现图片文件批量命名

《Python脚本实现图片文件批量命名》这篇文章主要为大家详细介绍了一个用python第三方库pillow写的批量处理图片命名的脚本,文中的示例代码讲解详细,感兴趣的小伙伴可以了解下... 目录前言源码批量处理图片尺寸脚本源码GUI界面源码打包成.exe可执行文件前言本文介绍一个用python第三方库pi
阅读更多...
Java中将异步调用转为同步的五种实现方法

Java中将异步调用转为同步的五种实现方法

《Java中将异步调用转为同步的五种实现方法》本文介绍了将异步调用转为同步阻塞模式的五种方法：wait/notify、ReentrantLock+Condition、Future、CountDownL... 目录异步与同步的核心区别方法一：使用wait/notify + synchronized代码示例关键
阅读更多...
golang字符串匹配算法解读

golang字符串匹配算法解读

《golang字符串匹配算法解读》文章介绍了字符串匹配算法的原理,特别是Knuth-Morris-Pratt（KMP）算法,该算法通过构建模式串的前缀表来减少匹配时的不必要的字符比较,从而提高效率,在... 目录简介KMP实现代码总结简介字符串匹配算法主要用于在一个较长的文本串中查找一个较短的字符串（称为
阅读更多...
Nginx实现动态封禁IP的步骤指南

Nginx实现动态封禁IP的步骤指南

《Nginx实现动态封禁IP的步骤指南》在日常的生产环境中,网站可能会遭遇恶意请求、DDoS攻击或其他有害的访问行为,为了应对这些情况,动态封禁IP是一项十分重要的安全策略,本篇博客将介绍如何通过NG... 目录1、简述2、实现方式3、使用 fail2ban 动态封禁3.1 安装 fail2ban3.2 配
阅读更多...
Java中实现订单超时自动取消功能(最新推荐)

Java中实现订单超时自动取消功能(最新推荐)

《Java中实现订单超时自动取消功能(最新推荐)》本文介绍了Java中实现订单超时自动取消功能的几种方法,包括定时任务、JDK延迟队列、Redis过期监听、Redisson分布式延迟队列、Rocket... 目录1、定时任务2、JDK延迟队列 DelayQueue（1）定义实现Delayed接口的实体类 （
阅读更多...
将java程序打包成可执行文件的实现方式

将java程序打包成可执行文件的实现方式

《将java程序打包成可执行文件的实现方式》本文介绍了将Java程序打包成可执行文件的三种方法：手动打包（将编译后的代码及JRE运行环境一起打包）,使用第三方打包工具（如Launch4j）和JDK自带... 目录1.问题提出2.如何将Java程序打包成可执行文件2.1将编译后的代码及jre运行环境一起打包2
阅读更多...
通俗易懂的Java常见限流算法具体实现

通俗易懂的Java常见限流算法具体实现

《通俗易懂的Java常见限流算法具体实现》：本文主要介绍Java常见限流算法具体实现的相关资料,包括漏桶算法、令牌桶算法、Nginx限流和Redis+Lua限流的实现原理和具体步骤,并比较了它们的... 目录一、漏桶算法1.漏桶算法的思想和原理2.具体实现二、令牌桶算法1.令牌桶算法流程:2.具体实现2.1
阅读更多...
MySQL8.0设置redo缓存大小的实现

MySQL8.0设置redo缓存大小的实现

《MySQL8.0设置redo缓存大小的实现》本文主要在MySQL8.0.30及之后版本中使用innodb_redo_log_capacity参数在线更改redo缓存文件大小,下面就来介绍一下,具有一... mysql 8.0.30及之后版本可以使用innodb_redo_log_capacity参数来更改
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2