让微积分穿梭于工作与学习之间（32）：平面上一点到圆弧直线的距离及其在趋于直线时的极限

对CAD圆弧直线不了解的朋友可以先阅读以下博文：

https://blog.csdn.net/iloveas2014/article/details/103837857

https://blog.csdn.net/iloveas2014/article/details/103848611

好久没来写博客了。因为我被人派去研究了别的东西，并且没有什么很独特的心得。

而点到圆弧直线的距离，则是一个比较小的需求（当然底层要经常用），在图形编辑器中用于实现吸附效果。

吸附的规则是，鼠标位置或者被移动对象到线条的距离小于等于某个给定值时，“鼠标”或者物体会被对齐到线条上，因此需要计算点到圆弧直线的距离才能实现。

假设直线的方程为

则给定点(x,y)到直线的距离为

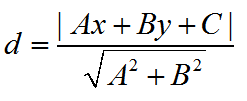
至于圆弧，书上并没有给出公式。不给出的原因大概是比较简单。给定点P到圆弧的距离正好等于P到圆心的距离和半径的差值，如下图所示。

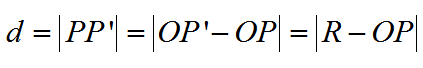
然后，我们把前面圆弧曲线的圆心公式和半径公式搬过来。同时给上图加上更多的标注方便说明。

另外给些中间常量会让演算过程看起来简洁点

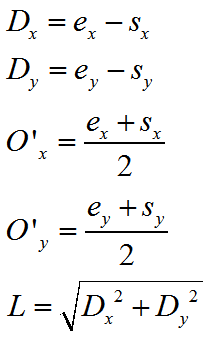
这样的话，圆心坐标和半径就分别等于

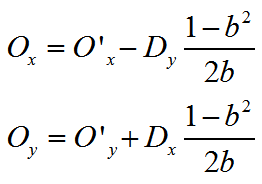
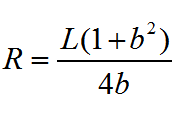
这些公式的推导可以回到15,16篇来回顾。

然后P就是给定点(x,y)

现在我们可以开始代入了

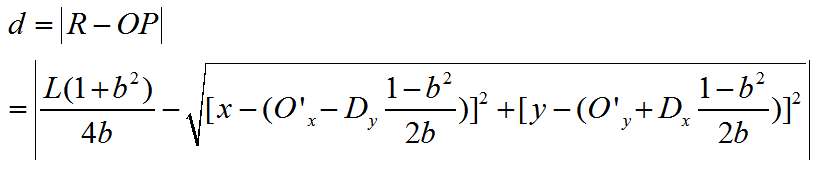
为了避免不必要的麻烦，在展开过程中，我们把绝对值号去掉，即

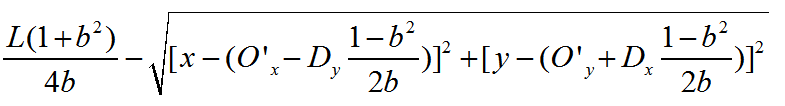
用有理化法去处理这个式子，发现虽然半径的表达式很简单，但由于格式跟点到圆心的距离公式差别太大，分子有理化后，分母的处理变得相当困难，所以为了这个事情，我一拖再拖，拖了足足一个月，每次难得忙里偷闲去试着推导都以失败告终。

为此我把半径换成起点（用终点也是一样）跟圆心的距离，即

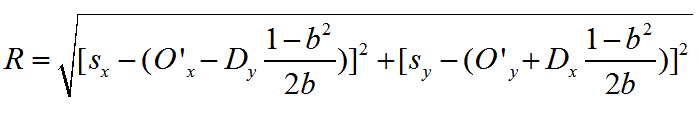
跟OP的区别仅仅是把x换成sx，把y换成了sy。经过这样的一个变通之后，虽然整个式子长了，但是整理起来却简单了不少，十几分钟就演算完了。

此处继续去掉绝对值号进行演算。

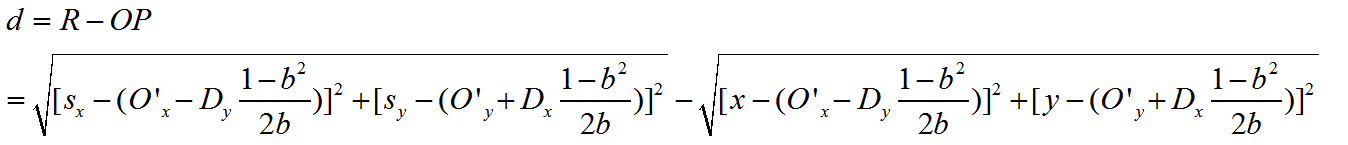
这么长的表达式，虽然我在草稿纸上是直接有理化的，但是贴到博客上发现看着蛋疼，所以，既然都用了圆心，那么有理化的时候还是先用Ox和Oy来表示圆心吧。

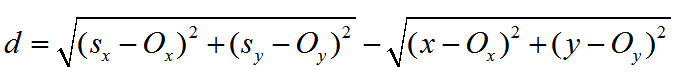
当然了，Ox和Oy最后还是要替换回去的，因为Ox和Oy都是跟b有关的变量。

经过这样的一波化简后，我们可以把Ox和Oy用带b的表达式套回去了。

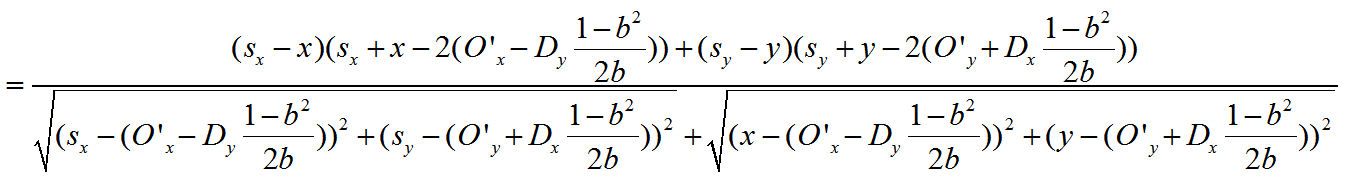
在上一篇，我们给出了有理化后分子分母除以x的技巧，那个地方的x是趋于无穷大的，而这里的b是趋于0，所以此处把除改成乘。

分子分母同时乘以b，得到

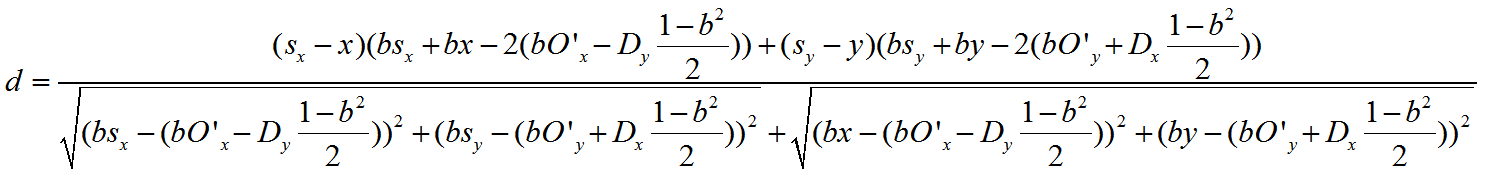
此时，b没再单独存在于分母里了，可以直接取极限。

这个过程很完美，无需使用夹逼公式，只要对b直接赋值即可得到距离在趋于直线时的极限。

现在我们把中间常量换回已知的条件

然后，我们通过直线的两点式求出直线一般方程的三个系数，看是否跟式子

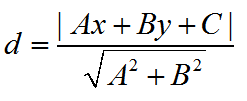
完全匹配。

把ABC三个值代入，得到

跟前面的结果对照下

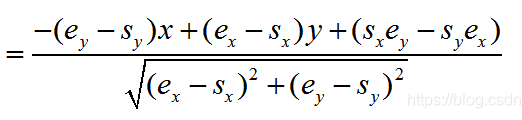
发现除了一个绝对值符号以外，其它东西完全一致。而前面我们提到，为了演算过程看起来更清晰，我们把绝对值号去掉了，只要补回去，结果就完全匹配了！

至此，我们正式算出了点到圆弧直线的距离公式，同时兼容直线和圆弧，且无需借助任何条件和夹逼公式。

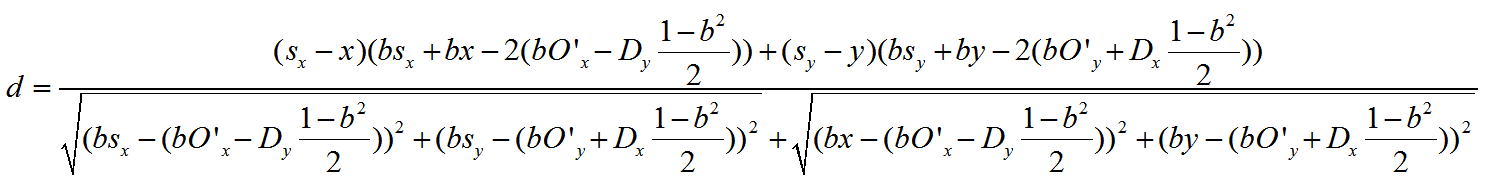
虽然无需通过条件进行区分，但是它的运算量比分开计算还大，所以在性能要求高的场合，还是不建议合着来写。除非要公式高度统一，或者做更深入的学术研究。

快过年了，祝大家新春快乐，牛气冲天，阖家幸福，我们明年见！