欧拉公式推导网格中点线面估计数量关系

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

背景

1. 之前面试网格算法工程师时被问到三角网格中点和面的数量关系。
2. delaunay 三角剖分要估计边的数量来事先申请内存。

通过查找资料了解原理和推导过程。

欧拉公式

欧拉公式描述如下：V、E和F分别是点、边和面的个数。 所有和一个球面同胚的多面体点边面的关系为：

$F-E+V=2$

半边数据结构

在计算机图形学中，习惯使用半边数据结构来表示网格。
一条边最多由2个面共享，把边分成正向和反向2条半边。
一共有2E个半边。

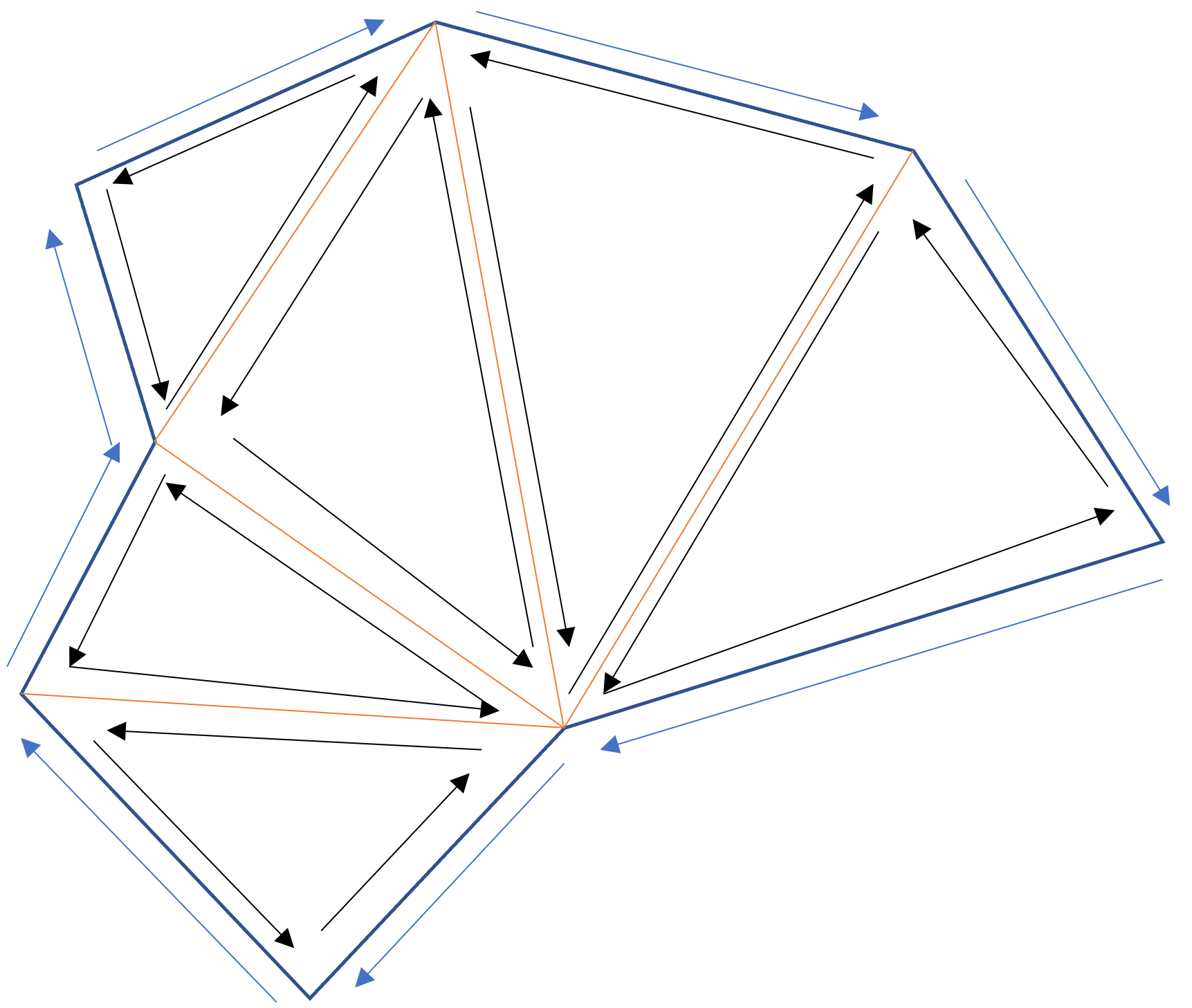
推导过程

根据半边数据结构可知，每个面有3个半边
一共有3F个半边。3F=2E=>E=3/2F。

代入欧拉公式替换E得到点与面关系
$-\frac{1}{2}F+V=2=>V=\frac{1}{2}F+2$

代入上述公式替换F得到点与边关系
$V=\frac{1}{3}E+2$

结论

面与边关系

$3F\approx 2E$

点与面关系

$2V\approx F$

点与边关系

$3V\approx E$

由于网格亏格的存在，以及网格中的边界，数量上不可能完全和上述公式吻合。所以这里只是一个大概情况。对于内存的估计和网格质量检查已经完全够用了。

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。