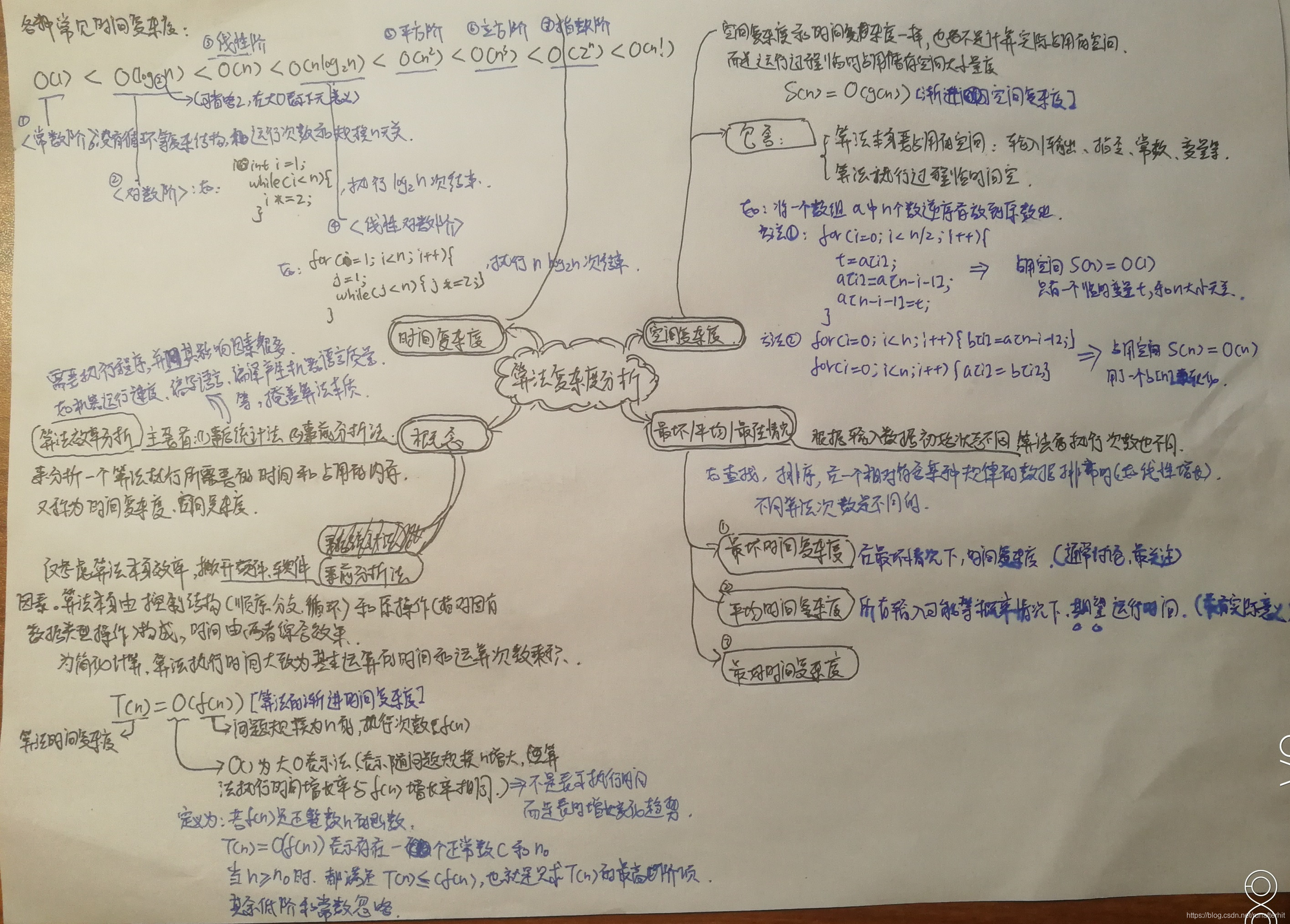
本文主要是介绍简图记录-算法复杂度分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、概念
1、算法执行效率
主要从 执行需要的时间(时间复杂度) 和 占用的存储空间(空间复杂度)分析 。
方式主要有:事后统计法 和 事前分析法。
2、事后统计法缺点
需要执行程序进行统计,由于其影响因素过多,比如 机器的运行速度、编译的语言、编译产生的机器语言质量等,掩盖了 算法分析的本质。
3、事前分析法概念
撇开 硬软件因素,仅讨论算法本身的执行效率。算法本身 由 控制结构(顺序、分支、循环)和 原操作(指对固有数据类型操作)构成,两者综合影响了算法的执行效率。
为了简化计算,算法的执行时间大致由一次基本运算的时间和运算次数的乘积得到。
事前分析法主要通过 大O表示法 来体现 随着问题规模的变化,算法执行效率的变化趋势,而非具体的实际执行效率。
4、大O表示法
例如时间复杂度的计算公式(算法的渐进时间复杂度):T(n) = O(f(n))。
n为问题的规模大小。f(n)表示执行次数。
O()为大O表示法,表示随着问题规模n增大,算法的执行时间增长率与f(n)增长率相同。
大O表示法定义:如f(n)是正整数n的函数,T(n) = O(f(n))表示存在一个正常数C和n0,当n>=n0时,都满足T(n) <= f(n),也就是T(n)只求最高阶项,其余低阶和常数忽略。
二、时间复杂度
算法的渐进时间复杂度:T(n) = O(f(n))
常见的时间复杂度举例(从小到大):
常数阶 O(1) 没有循环等复杂结构,运行次数和规模n无关。
对数阶 O(logn) 执行与logn正相关,如:
i = 1
while (i < n) { i *=2; }
线性阶 O(n)
for (int i = 0; i < n; i++) {j++;
}
线性对数阶 O(nlogn)
for (int i = 0; i < n; i++) {int j = 1while (j < n) { j *=2; }
}
平法阶 O(n^2)
立方阶 O(n^3)
指数阶 O(2^n)
三、空间复杂度
算法的渐进空间复杂度:S(n) = O(g(n))
影响因素:1、算法本身要占用的空间 输入/输出,指令,常数,变量等。2、算法执行过程临时空间。
常见的空间复杂度举例,例如 将一个 数组a中n个数 逆序 存储:
常数阶 O(1)
for (i = 0; i < n/2; i++) {tmp = a[i]; //只使用了一个临时变量 用来变换a[i] = a[n - 1 - i];a[n - 1 - i] = tmp;
}
线性阶 O(n)
for (i = 0; i < n; i++) { b[i] = a[n - 1 - i]; } // 使用了一个b[n]数组来反转
for (i = 0; i < n; i++) { a[i] = b[i]; }
四、最坏/平均/最好 情况
根据输入数据初始状态不同,算法的执行次数和空间也会不同。例如 排序算法,输入数据规律不同,决定了选择算法类型执行的次数不同。 算法分析主要由以下三种情况(以时间复杂度举例)。
1、最坏 时间 复杂度
最坏的情况下,时间复杂度,也就是最高阶执行操作的最大执行次数。通常情况大家讨论时间复杂度 都是 讨论这个问题,最关注这个。
2、平均 时间 复杂度
在所有输入可能概念相同的情况,算法执行时间的数学期望(最具实际意义)。
3、最好 时间 复杂度
这篇关于简图记录-算法复杂度分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







