二叉树的前序、中序、后序、层序遍历，递归和迭代两大类解题思路，每类细分不同解法【完整版】附PDF文档

二叉树文章系列：

1. 二叉树的前序遍历
2. 二叉树的中序遍历
3. 二叉树的后序遍历
4. 二叉树的层序遍历
5. 二叉树的前序、中序、后序、层序遍历【解法完整版】

一、二叉树的前序遍历

二叉树的前序遍历的记忆法则是“根左右"，即先遍历根节点，再遍历左子树节点，再遍历右子树节点。

以上图为例，前序遍历的结果是【A, B, D, E, C, F, G】

1.1 解题思路：递归

递归是我们实现前中后序遍历最常用的方法。

什么问题可以采用递归求解呢？

需要满足三个条件：

1. 一个问题的解可以分解为若干个子问题的解；
2. 这个问题与分解的子问题，除了数据规模不同外，求解思路相同
3. 存在递归终止条件。

那么在知道一个问题可以采用递归实现之后，如何写出递归代码呢？

关键在于能写出递归公式，找到终止条件。

在二叉树的前序遍历问题上，它的递归公式是:

preorder(node) = print node —> preorder(node->left) --> preorder(node->right)

它的终止条件是：

node 是否为空，为空则返回。

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;preorder(res, root);return res;}void preorder(vector<int>& res, TreeNode* root){if(!root) return;res.emplace_back(root->val);preorder(res, root->left);preorder(res, root->right);}
};

1.2 解题思路：迭代（方法1）

在递归方法实现过程中，它的底层是基于系统栈的结构来实现的。因此，我们可以使用栈的数据结构来辅助实现基于迭代方式的前序遍历。

具体思路为：

• 初始化栈stack，初始化输出列表res
• 根节点入栈
• while(栈不为空)，在循环体内部：
  • 栈顶元素出栈
  • 栈顶元素添加到输出列表
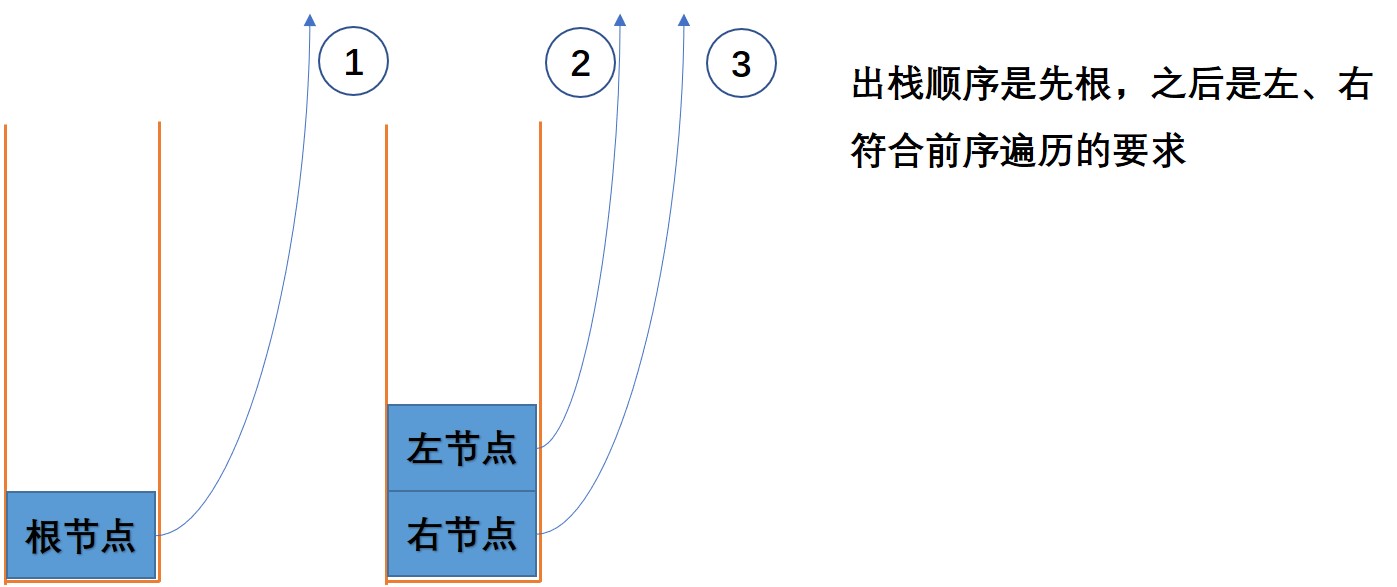
  • 如果栈顶元素的右子树节点不为空，将右子树节点入栈
  • 如果栈顶元素的左子树节点不为空，将左子树节点入栈
• 返回输出列表res

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;stack<TreeNode*> s;s.push(root);while(!s.empty()){TreeNode* node = s.top();s.pop();res.emplace_back(node->val);if(node->right) s.push(node->right);if(node->left) s.push(node->left);}return res;}
};

1.3 解题思路：迭代（方法2）

基于迭代方法的第二种思路如下：

• 初始化栈stack，初始化输出列表res
• 设置一个变量cur, 表示当前节点。并赋初始值为根节点root
• while(栈不为空 或者 当前节点cur不为空)，在循环体内部：
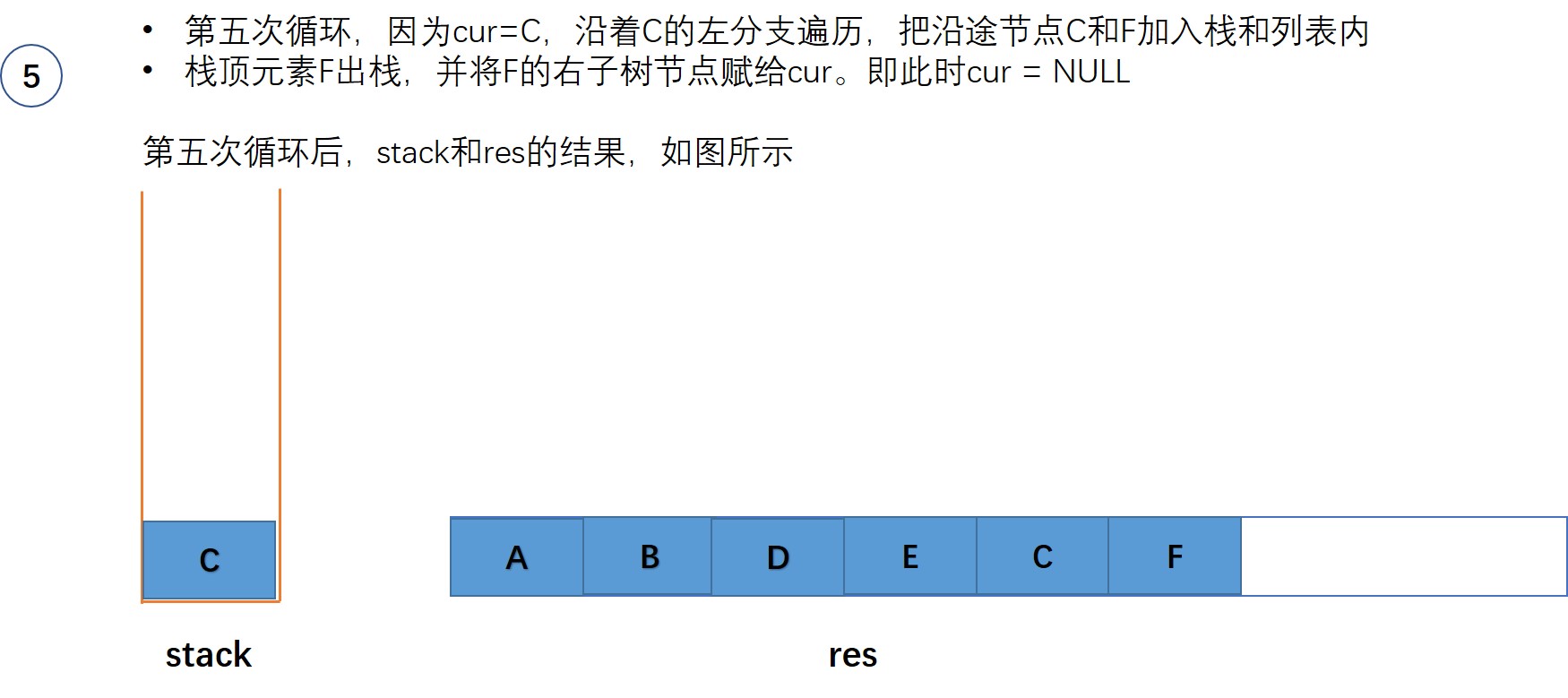
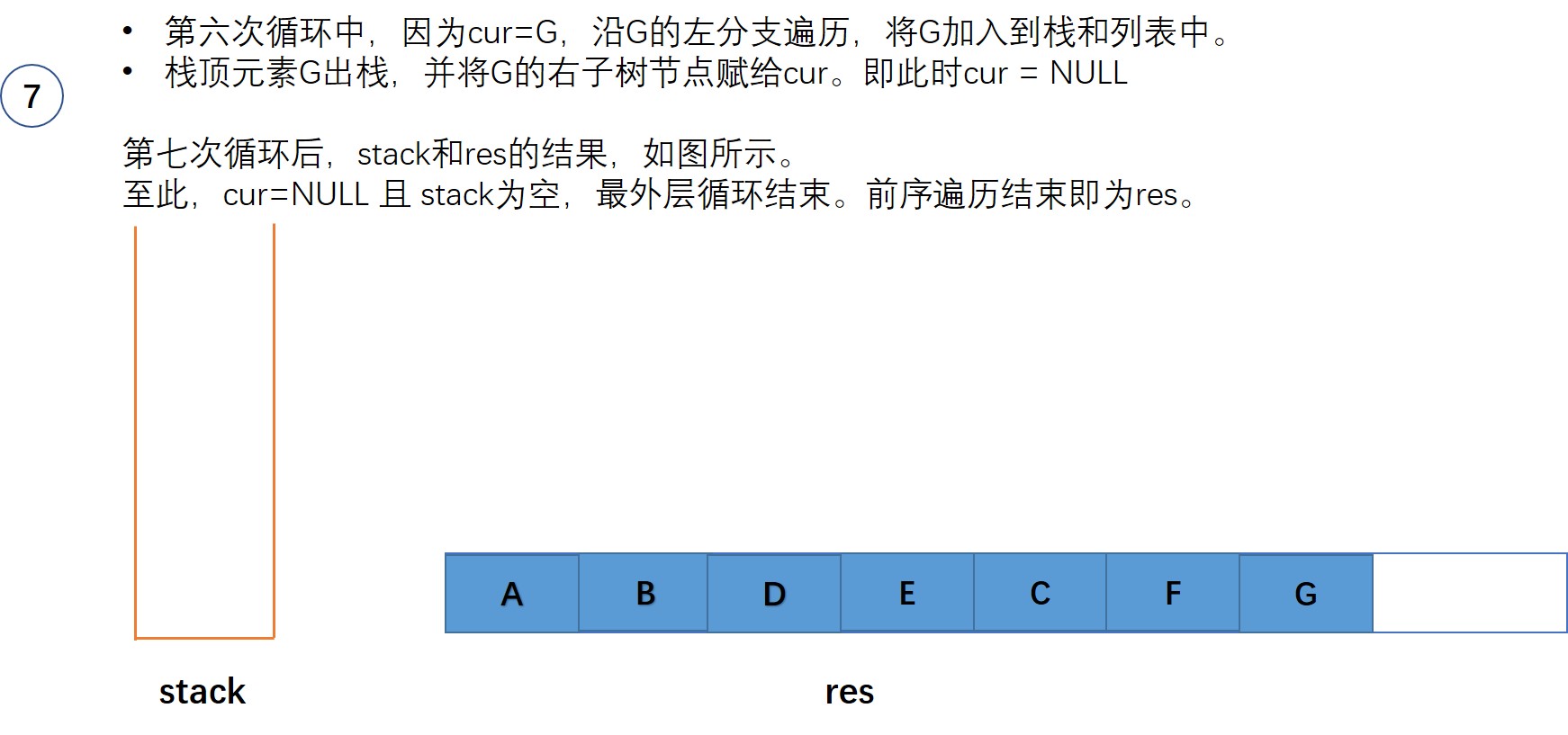
  • 沿着当前节点的左分支一直走，直到为空。在这个过程中将遍历的节点都入栈，同时添加到输出列表
  • 栈顶元素出栈
  • 更新当前节点cur为栈顶元素的右子树节点。
• 返回输出列表res

以图中的二叉树为例，来一步步来展示这个过程：

初始时，当前节点cur = root ，即节点A

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;TreeNode* cur = root;stack<TreeNode*> s;while(!s.empty() || cur){// 沿着当前节点cur的左分支一直走到底while(cur){s.push(cur);res.emplace_back(cur->val);cur = cur->left;}TreeNode* node = s.top();s.pop();cur = node->right;}return res;}
};

二、二叉树的中序遍历

二叉树的中序遍历的记忆法则是“左根右"，即先遍历左子树节点，再遍历根节点，再遍历右子树节点。

以上图为例，中序遍历的结果是【D, B, E, A, F, C, G】

2.1 解题思路：递归

递归是我们实现前中后序遍历最常用的方法。

什么问题可以采用递归求解呢？

需要满足三个条件：

1. 一个问题的解可以分解为若干个子问题的解；
2. 这个问题与分解的子问题，除了数据规模不同外，求解思路相同
3. 存在递归终止条件。

那么在知道一个问题可以采用递归实现之后，如何写出递归代码呢？

关键在于能写出递归公式，找到终止条件。

在二叉树的中序遍历问题上，它的递归公式是:

preorder(node) = preorder(node->left) --> print node —> preorder(node->right)

它的终止条件是：

node 是否为空，为空则返回。

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;inorder(res, root);return res;}void inorder(vector<int>& res , TreeNode* root){if(!root) return; inorder(res, root->left);res.emplace_back(root->val);inorder(res, root->right);}
};

2.2 解题思路：迭代

基于迭代方法的思路如下：

• 初始化栈stack，初始化输出列表res
• 设置一个变量cur, 表示当前节点。并赋初始值为根节点root
• while(栈不为空 或者 当前节点cur不为空)，在循环体内部：
  • 沿着当前节点的左分支一直走，直到为空。在这个过程中将遍历的节点都入栈
  • 栈顶元素出栈，同时将栈顶元素添加到输出列表
  • 更新当前节点cur为栈顶元素的右子树节点。
• 返回输出列表res

以图中的二叉树为例，来一步步来展示这个过程：

初始时，当前节点cur = root ，即节点A

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;stack<TreeNode* > s;TreeNode* cur = root;while(!s.empty() || cur){// 沿着当前节点cur的左分支一直走到底while(cur){s.push(cur);cur = cur->left;}TreeNode* node = s.top();s.pop();res.emplace_back(node->val);cur = node->right;}return res;}
};

三、二叉树的后序遍历

二叉树的后序遍历的记忆法则是“左右根"，即先遍历左子树节点，再遍历右子树节点，最后遍历根节点。

以上图为例，后序遍历的结果是【D, E, B, F, G, C, A】

3.1 解题思路：递归

递归是我们实现前中后序遍历最常用的方法。

什么问题可以采用递归求解呢？

需要满足三个条件：

1. 一个问题的解可以分解为若干个子问题的解；
2. 这个问题与分解的子问题，除了数据规模不同外，求解思路相同
3. 存在递归终止条件。

那么在知道一个问题可以采用递归实现之后，如何写出递归代码呢？

关键在于能写出递归公式，找到终止条件。

在二叉树的前序遍历问题上，它的递归公式是:

preorder(node) = preorder(node->left) --> preorder(node->right) —> print node

它的终止条件是：

node 是否为空，为空则返回。

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;preorder(res, root);return res;}void preorder(vector<int>& res, TreeNode* root){if(!root) return;res.emplace_back(root->val);preorder(res, root->left);preorder(res, root->right);}
};

3.2 解题思路：迭代（方法1）

我们在使用迭代法来实现后序遍历的时候，通常有两大类思路。第一类是先得到“根右左”，然后对输出列表反序，即得到“左右根”； 第二类是直接求出“左右根”。

咱们知道，前序遍历是求“根左右”，那么我们可以使用前序遍历的方法，去求得“根右左”。以上图为例，我们求得的“根右左”的结果是【A, C, G, F, B, E, D】。再对这个结果反序，得到【D, E, B, F, G, C, A】。这正是咱们想得到的后序遍历。

本文第二节和第三节介绍的两种迭代方法，都是采用这种思路来实现。最后第四小节，我们会介绍直接求出后序遍历的思路。

---

在递归方法实现过程中，它的底层是基于系统栈的结构来实现的。因此，我们可以使用栈的数据结构来辅助实现基于迭代方式的后序遍历。

具体思路为：

• 初始化栈stack，初始化输出列表res
• 根节点入栈
• while(栈不为空)，在循环体内部：
  • 栈顶元素出栈
  • 栈顶元素添加到输出列表
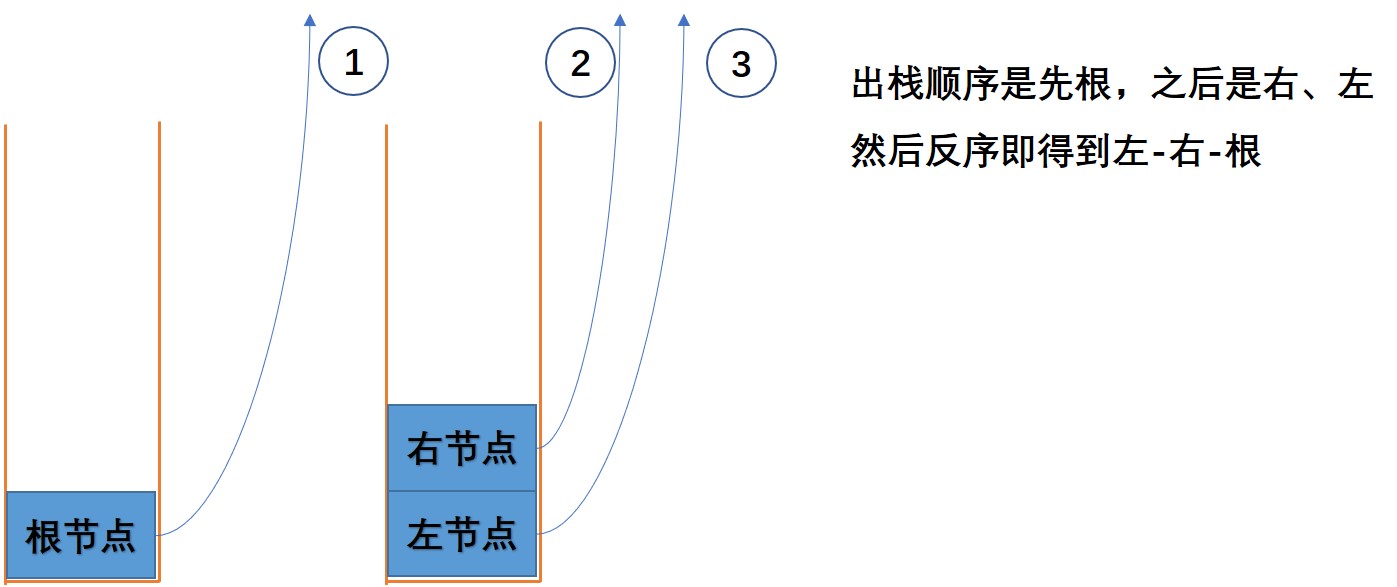
  • 如果栈顶元素的左子树节点不为空，将左子树节点入栈
  • 如果栈顶元素的右子树节点不为空，将右子树节点入栈
• 对输出列表res 进行反序
• 返回输出列表res

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;stack<TreeNode*> s;s.push(root);while(!s.empty()){TreeNode* node = s.top();s.pop();res.emplace_back(node->val);if(node->left) s.push(node->left);if(node->right) s.push(node->right);}reverse(res.begin(), res.end());return res;}
};

3.3 解题思路：迭代（方法2）

基于迭代方法的第二种思路如下：

• 初始化栈stack，初始化输出列表res
• 设置一个变量cur, 表示当前节点。并赋初始值为根节点root
• while(栈不为空 或者 当前节点cur不为空)，在循环体内部：
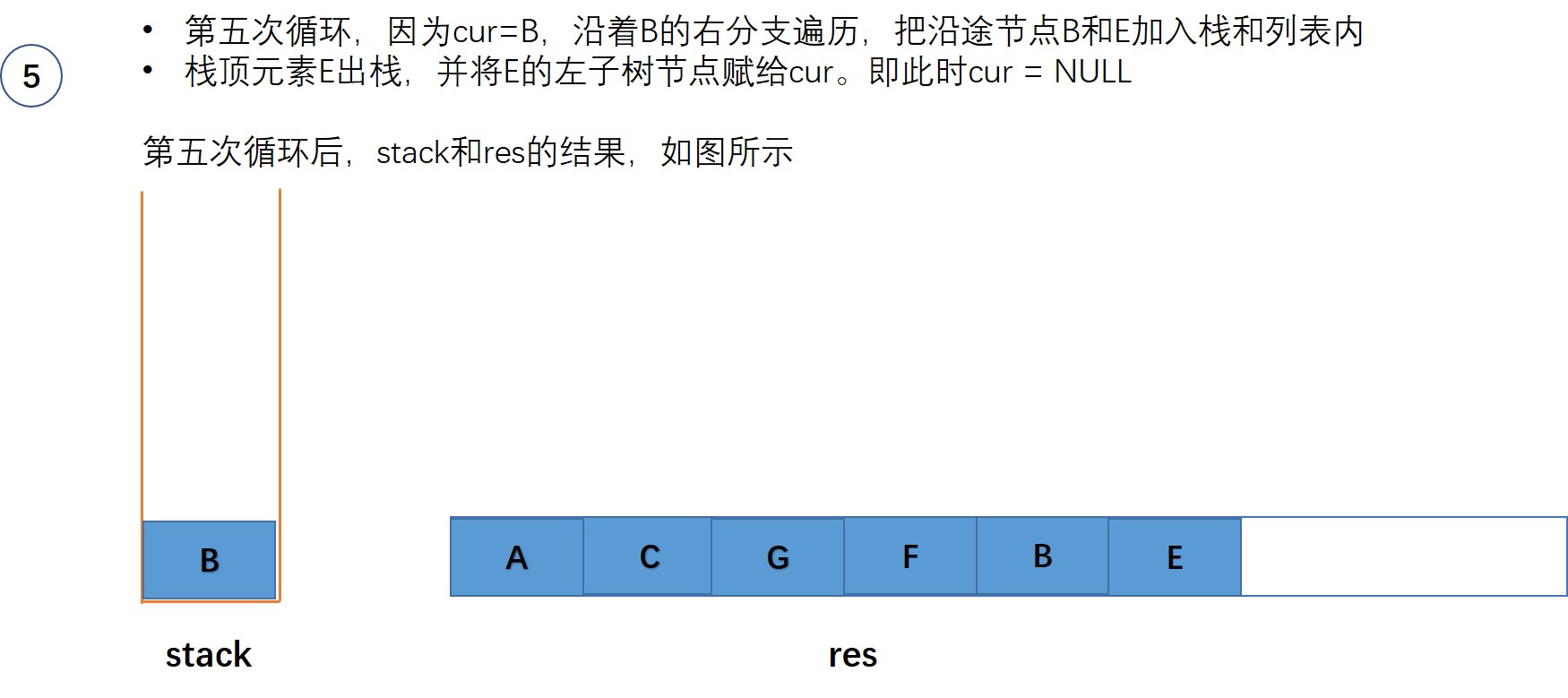
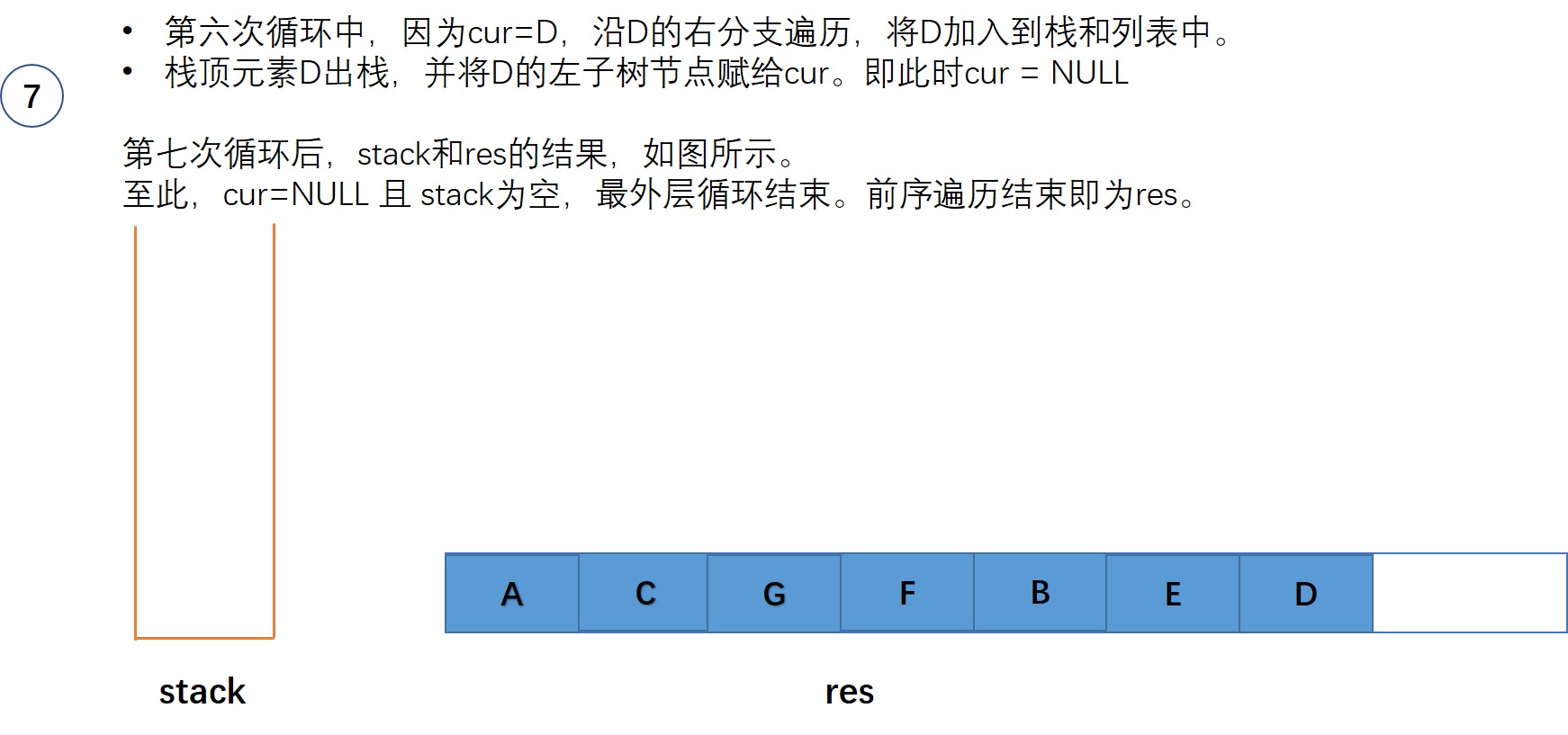
  • 沿着当前节点的右分支一直走，直到为空。在这个过程中将遍历的节点都入栈，同时添加到输出列表
  • 栈顶元素出栈
  • 更新当前节点cur为栈顶元素的左子树节点。
• 对输出列表res 进行反序
• 返回输出列表res

以图中的二叉树为例，来一步步来展示这个过程：

初始时，当前节点cur = root ，即节点A

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;stack<TreeNode*> s;TreeNode* cur = root;while(!s.empty() || cur){while(cur){res.emplace_back(cur->val);s.push(cur);cur = cur->right;}TreeNode* node = s.top();s.pop();cur = node->left;}reverse(res.begin(), res.end());return res;}
};

3.4 解题思路：迭代（方法3）

这次我们要尝试直接得到后序遍历的结果。

我们知道后序遍历的顺序是”左右根“。那么对于一个根节点，要先遍历它的左子树节点和右子树节点，再回头遍历根节点。

为了防止遍历根节点的时候，再次遍历到它的左、右子树节点；我们需要一个变量，来表示最后一次出栈的元素。

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;if(!root) return res;stack<TreeNode* > s;s.push(root);TreeNode* lastPopNode = root;while(!s.empty()){TreeNode* node = s.top();if(node->left && node->left != lastPopNode && node->right != lastPopNode){s.push(node->left);}else if(node->right && node->right != lastPopNode){s.push(node->right);}else{res.emplace_back(node->val);s.pop();lastPopNode = node;}}return res;  }
};

四、二叉树的层序遍历

4.1 解题思路：广度优先搜索BFS

广度优先搜索是从树的根节点开始，沿着树的宽度来遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索通常采用队列来辅助实现。

在题目中要求按照层序遍历，实现逐层地从左向右访问所有的结点。这正好符合广度优先搜索的策略。

我们可以立即想到普通广度优先搜索的模板：

vector<int> bfs(TreeNode* root) {std::vector<int> result;if(!root){return result;}   queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode* node = q.front();q.pop();result.emplace_back(node->val);if(node->left){q.push(node->left);}            if(node->right){q.push(node->right);}}return result;
}	

但是，这里返回的是一个一维数组，和题目要求的二维数组不一致。因此，我们需要稍作修改，修改内容如下：

• 在while循环每次遍历时，获取队列的长度N（即队列中的节点个数）
• 一次性的处理这N个节点，然后再进入下一轮循环。

通过这种修改，确保每次循环时要处理的队列中元素都是本层的元素。

vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;if(!root){return result;}queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> tmp;// 每次q.size() 获取的都是队列的长度（一个层的节点个数）for(int i = q.size(); i > 0 ; i--){TreeNode* node = q.front();q.pop();tmp.emplace_back(node->val);if(node->left) q.push(node->left);if(node->right) q.push(node->right);}result.emplace_back(tmp);}return result;}

4.2 解题思路：深度优先搜索DFS

本题也可以使用深度优先搜索来实现。

深度优先搜索是采用栈或者递归来实现。（递归在系统内部也是基于栈来实现）

vector<vector<int>> levelOrder(TreeNode* root) {std::vector<std::vector<int>> res;if(!root) return res;dfs(0, root, res);return res;
}// index 是节点所在层的层索引
void dfs(int index, TreeNode* node, std::vector<std::vector<int>>& res){// node 应该放到res[index]中, 如果res[index]元素不存在, 需要先创建一个if(res.size() < index + 1){res.push_back({});}res[index].emplace_back(node->val);if(node->left){dfs(index+1, node->left, res);}if(node->right){dfs(index+1, node->right, res);}
}

后记：
我将以上内容整理成一份PDF文档，需要的朋友可以加我微信好友【xinglunan_0608】找我要一份