本文主要是介绍python 编程求矩阵运算及求多元一次方程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 一、python 矩阵操作
- 二、python 矩阵乘法
- 三、python 矩阵转置
- 四、python 求方阵的迹
- 五、python 方阵的行列式计算方法
- 六、python 求逆矩阵 / 伴随矩阵
- 七、python 解多元一次方程
本文内容:使用 jupyter 编写 python 代码对矩阵进行基本运算。
一、python 矩阵操作
- 先引入 numpy ,以后的教程中,我们都引用 np 作为简写。
- 使用 mat 函数创建一个 2×3 矩阵。
#引入numpy
import numpy as np
#使用mat函数创建一个2×3矩阵
a=np.mat([[1,2,3],[4,5,6]])
a

- 使用 shape 可以获取矩阵的大小。
#使用shape可以获取矩阵的大小
a.shape

- 使用下表读取矩阵中的元素
#使用下标读取矩阵中的元素
a.T

- 进行行列转换。
#进行行列转换
a.transpose()a.T

- 实际上官方文档建议我们使用二维数组代替矩阵来进行矩阵运算;因为二维数组用得较多,而且基本可取代矩阵。
#用二维数组代替矩阵
b=np.array([[1,2,3],[4,5,6]])
bb.T

- 加减法也是一样的。
#加减法
a+ab+b

- 当然列表是不能这么尽兴加减的。
#列表不能尽兴加减
c=[[1,2,3],[4,5,6]]
c+c

二、python 矩阵乘法
- 使用二维数组创建两个矩阵 A 和 B。
#使用二维数组创建两个矩阵A和B
A=np.array([[1,2,3],[4,5,6]])
B=A.TAB

- 先来一个矩阵的数乘,其实是矩阵的每一个元素乘以该数。
#矩阵每个元素乘以该数
2*A2*B

- dot 函数用于矩阵乘法,对于二维数组,它计算的是矩阵乘积,对于一维数组,它计算的是内积。
A*Bnp.dot(A,B)np.dot(B,A)

- 再创建一个二维数组
#创建一个二维数组
C=np.array([[1,2],[1,3]])
C

- 我们验证一个矩阵乘法的结合性:(AB)C=A(BC)。
#验证矩阵乘法的结合性 (AB)C=A(BC)
np.dot(np.dot(A,B),C)np.dot(A,np.dot(B,C))

- 接着看一下对加法的分配性:(A+B)C=AC+BC、C(A+B)=CA+CB。
#验证加法的分配性 (A+B)C=AC+BC C(A+B)=CA+CB
D=B-1
Dnp.dot(A,B+D)np.dot(A,B)+np.dot(A,D)

- 数乘的结合性,也是一样的。
#验证数乘的结合性
2*(np.dot(A,B))np.dot(A,2*B)np.dot(2*A,B)np.dot(A,2*B)

- 接着我们用到一个新知识,使用 eye 创建一个单位矩阵。
#使用 eye 创建一个单位矩阵
I=np.eye(3)
I

- 一个矩阵 A 乘以一个单位矩阵,还是它本身。
#矩阵 A 乘以一个单位矩阵
np.dot(A,I)

三、python 矩阵转置
- 先创建一个矩阵 A(前面已经创建过了)。
A

- 我们使用属性 T 来得到矩阵 A 的转置矩阵
A.T

- 验证第一个性质:(A’)’=A。
A.T.T

- 创建两个尺寸相同的矩阵(前面已经创建过了)。
BD

- 验证矩阵转置的第二个性质:(A±B)’=A’±B’。
(B+D).TB.T+D.T

- 验证矩阵转置的第三个性质:(KA)’=KA’
10*A.T(10*A).T

- 验证矩阵转置的第四个性质:(A×B)’=B’×A’
np.dot(A.T,B.T)np.dot(B.T,A.T)

四、python 求方阵的迹
- 方阵的迹就是主对角元素之和。
- 创建一个方阵(行数等于列数的矩阵)。
E=np.array([[1,2,3],[4,5,6],[7,8,9]])
E
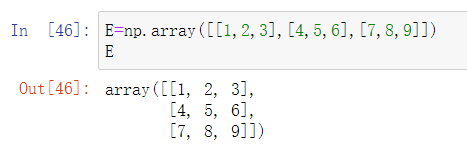
- 用 trace 计算方阵的迹。
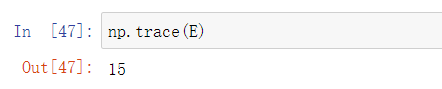
np.trace(E)
- 再创建一个方阵 F。
F=E-2
F

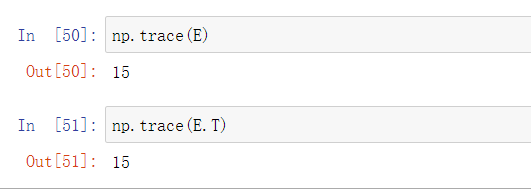
- 验证一下方阵的迹等于方阵的转置的迹。
np.trace(E)np.trace(E.T)
- 验证一下方阵的乘积的迹。
np.trace(np.dot(E,F))np.trace(np.dot(F,E))

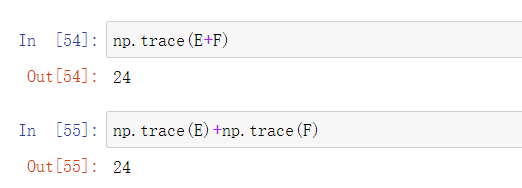
- 验证一下方阵的和的迹等于方阵的迹的和。
np.trace(E+F)np.trace(E)+np.trace(F)
五、python 方阵的行列式计算方法
- 如何计算方阵的行列式,用到的是 numpy 模块的 linalg.det 方法。
- 行列式计算方法:


- 创建两个方阵(上面已经创建过了)。
EF

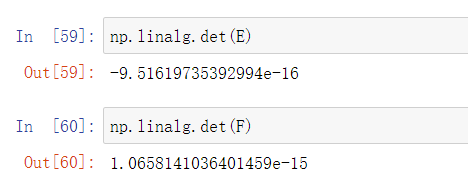
- 使用 det 方法求得方阵 E 和方阵 F 的行列式。
np.linalg.det(E)np.linalg.det(F)
Cnp.linalg.det(C)

六、python 求逆矩阵 / 伴随矩阵
- 设 A 是数域上的一个 n 阶方阵,若在相同数域上存在另一个 n 阶矩阵 B,使得:AB=BA=E,则我们称 B 是 A 的逆矩阵,而 A 则被称为可逆矩阵,当矩阵 A 的行列式 |A| 不等于 0 时才存在可逆矩阵。

- 创建一个方阵。
A=np.array([[1,-2,1],[0,2,-1],[1,1,-2]])
A

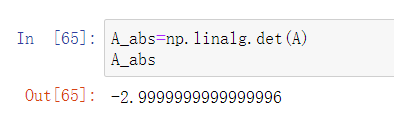
- 使用 linalg.det 求得方阵的行列式。
A_abs=np.linalg.det(A)
A_abs
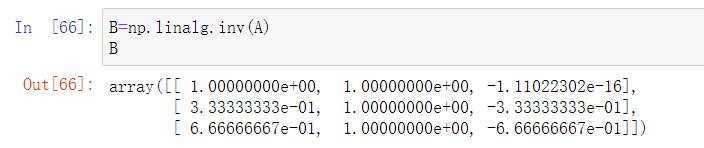
- 使用 linalg.inv 求得方阵 A 的逆矩阵。
B=np.linalg.inv(A)
B
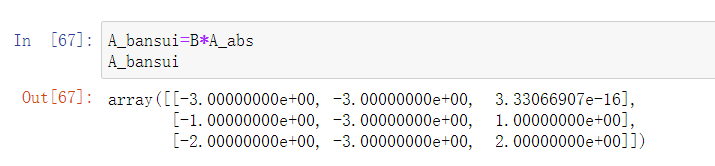
- 接着我们利用公式: A − 1 = A ′ ′ / ∣ A ∣ A^{-1}=A''/|A| A−1=A′′/∣A∣ ——> A ′ ′ = A − 1 ∣ A ∣ A''=A^{-1}|A| A′′=A−1∣A∣ 来计算。
A_bansui=B*A_abs
A_bansui
七、python 解多元一次方程
- 用 python 的 numpy 包中的 linalg.solve() 方法解多元一次方程。
- 首先看一下我们要解的方程,将这个方程格式调整好,按照 x-y-z-常数项的顺序排列:
x + 2 y + z = 7 2 x − y + 3 z = 7 3 x + y + 2 z = 18 x+2y+z=7\\ 2x-y+3z=7\\ 3x+y+2z=18 x+2y+z=72x−y+3z=73x+y+2z=18 - 将未知数的系数写下来,排列成一个矩阵 a ,如下:
a=[[1,2,1],[2,-1,3],[3,1,2]]
a=np.array(a)
a

- 常数项构成一个一维数组(向量)。
b=[7,7,18]
b=np.array(b)
b

- 使用linalg.solve 方法解方程,参数 a 指的是系数矩阵,参数 b 指的是常数项矩阵。
x=np.linalg.solve(a,b)
x

- 使用点乘的方法可以验证一下,系数乘以未知数可以得到常数项。
np.dot(a,x)

这篇关于python 编程求矩阵运算及求多元一次方程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




