本文主要是介绍字母预言卡里的魔术与数学(三)——魔术背后的数学模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
爱学习,勤思考;学数学,玩魔术。欢迎点击头部蓝字关注MatheMagician,这里有你要的奇迹!
在前面的文章中,我们分别探讨了《字母预言卡》这个魔术的表演改进以及背后数学模型建立的分析。今天,我们接着上一期的分析来把这个魔术背后的数学模型精确地描述出来,并完成求解。
相关内容回顾请戳:
魔术表演回顾
视频1 字母预言卡
问题回顾
如果选项有m个,至少需要几张卡片可以得到这个结果?或者反过来,n张卡片,最多可以容纳几个选项?以及,怎么设计每张卡片的选项有无的组合,才能够满足要求呢?这个卡片的各个选项出现的结果是否是唯一的,还是,存在很多组满足要求的解?
模型建立
我们来用数学语言描述一下,要完成预测选项需要的效果,这个每张卡片上每个元素的出现与否的组合,到底需要怎样的性质呢?
对于一系列满足要求的卡片设计,实际上是这么一个问题:给定m个元素e1,2…m,n个该m个元素构成集合的子集S1,2,…n,求解这样的{Sn},使得对任意的元素ei和ej,有如下式子成立,全部写成公式就是:
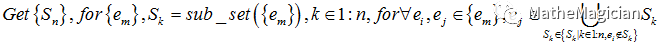
(这里属于符号表达的意思其实是取遍右边集合的元素)
这里,我们对给定的n,构造的上界m =C(n, [n / 2]),构造的解是:
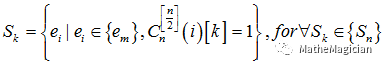
其中组合函数C(i)表示组合数的第i个用二进制数表达的解的具体值。
那这个构造解到底能不能够满足上面的条件呢?
估计你已经看晕了,我在分析这个问题到这里的时候,也是晕的。这到底怎么描述和验证这个解到底是不是满足要求的可行解呢?
好的数学是不会让人晕的,这里为什么会晕呢?
还是要回到基本概念。这里我用定长二进制数来表示集合,实际上用到了集合的本质属性,那就是全集到bool集合的映射,这种映射是后面各种函数,单射,双射,图等各类关系的起源。在这里还有m个元素,所以相当于某个卡片上的某个元素的bool值结果是由两个索引得到的,分别是卡片编号和元素编号,我们除了可以把每张卡片上的所有元素的bool值结果看成一系列以元素全集为基础的子集集合,也可以把每个元素本身在所有卡片上的bool值看作是以卡片全集为基础的子集集合。
以m = 6,n = 4为例的横纵两个索引的元素出现与否的示例,其中纵向就是Si集合,横向除了是元素本身,也可以看作是一组集合。如图所示:
图1 双索引集合示例
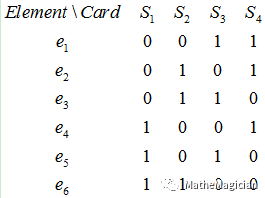
到此为止,我终于理解了苏东坡先生那首诗的含义了:横看成岭侧成峰,远近高低个不同,不识庐山真面目,只缘身在此山中。
前面的模型,都是直觉化的以卡片为集合的索引来理解的,如果以字母为索引呢?如果以字母为索引,那原题的要求立马化为:
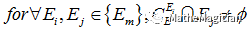
这里E指的是卡片全集,{Em}是所有卡片的子集,按照集合就是全集到bool值的映射,恰好对应上图的每一横牌的元素信息。
这个式子 比前面简单多了,但是也不容易解决,其实,我们画一下Wenn图就知道,下面的式子是成立的:
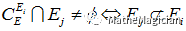
所以,我们只要证明,{Em}中的元素,两两互不包含就可以了。
这是显然的,因为作为组合结果,每个组合的元素数量是一样的,如果一个包含另一个,那之后可能两个集合相等,这就是同一个集合了,否则元素就不可能一样多。这就构成了矛盾,由反证法得证。
当数学家把魔术背后的数学研究清楚,魔术师已经拿着这个原理做成产品卖到全世界并开启巡回演出了……
以上,我们证明了我们通过组合数方法给出的解的可行性以及从信息论角度说明了这就是唯一的最优解。构造解和证明可行这步没有什么问题,但是为什么这就是最优解的证明是从信息论角度说明的,有些同学可能觉得仍然有点直觉。那么接下来,我们从数学角度,给出更严谨的证明,现在问题转化如下:
大小为n一个集合两两不不想交的子集的最大数量是C(n, [n / 2])。
这个命题是一个在离散数学中研究Extremal Set Theory中的一个重要结论。现卖个关子,感兴趣的同学可以把证明思路留言或者私信与我交流,期待看到大家的答案!
我们下一期最后一篇文章来公布证明过程以及其中美丽的数学!
本公众号现不定期放送数学和魔术相关学习资料,都是作者精心筛选整理后准备给大家的精华内容!现在进入公众号后台:
回复“数学”,获取《数学建模算法与应用》,数模比赛经典教材,司守奎著
回复“数学2”,获取《Pattern Recognition and Machine Learning》,机器学习和模式识别领域的圣经,英文原版
回复“魔术3”,获取magic2728本人魔术基础教学:《Double Lift讲解》
回复“魔术4”,获取magic2728本人魔术表演作品:《混沌的世界》
好了,今天数学魔术师的分享就到这里,希望各位客官喜欢,期待您的转发和赞赏哦!
更多精彩内容欢迎扫描下方二维码关注我们,下期再见!
我们是谁:
MatheMagician,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。我们既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖互联网,计算机,统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程鉴赏等魔术内容;以及结合二者的数学魔术分享。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎在文末或公众号留言与我交流!
推荐阅读:
点击阅读原文,往期精彩不错过!
这篇关于字母预言卡里的魔术与数学(三)——魔术背后的数学模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







