Carson带你学数据结构：手把手带你全面优化快速排序算法

前言

本文主要讲解排序算法中的快速排序 算法，希望你们会喜欢。

---

目录

---

1. 简介

---

2. 算法原理

步骤1：将待排序列 分割成独立的2个子序列

• 在待排序 序列中选择1个基准数据元素（第1个 / 最后1个，称为：枢轴）
• 通过比较 基准数据元素 与 序列其余元素 大小，将待排序列分成2部分：（右序列）1部分 > 基准元素、（左序列）1部分 ＜ 基准元素

步骤2：通过递归，分别对这2个子序列 进行快速排序

通过步骤2的方式，最终达到整个序列有序的目的

---

3. 算法示意图

初始状态

待排序序列 = {50,10,90,30,70,40,80,60,20}

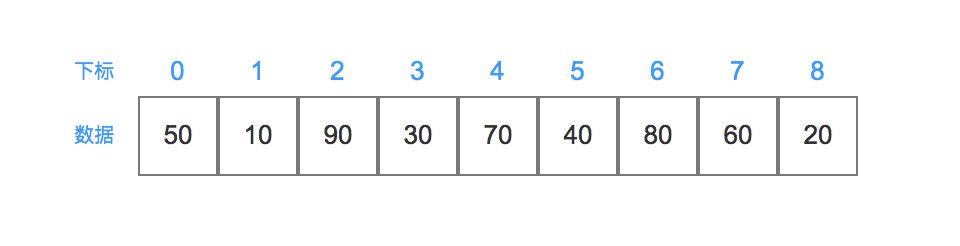
步骤1： 将待排序列 分割成独立的2个子序列

a. 在待排序 序列中选择1个基准数据元素（此处选第1个）

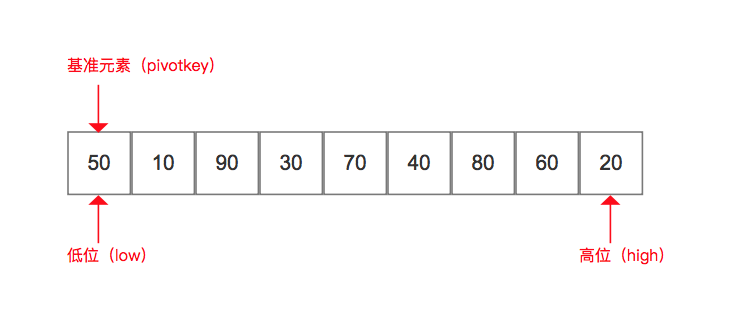
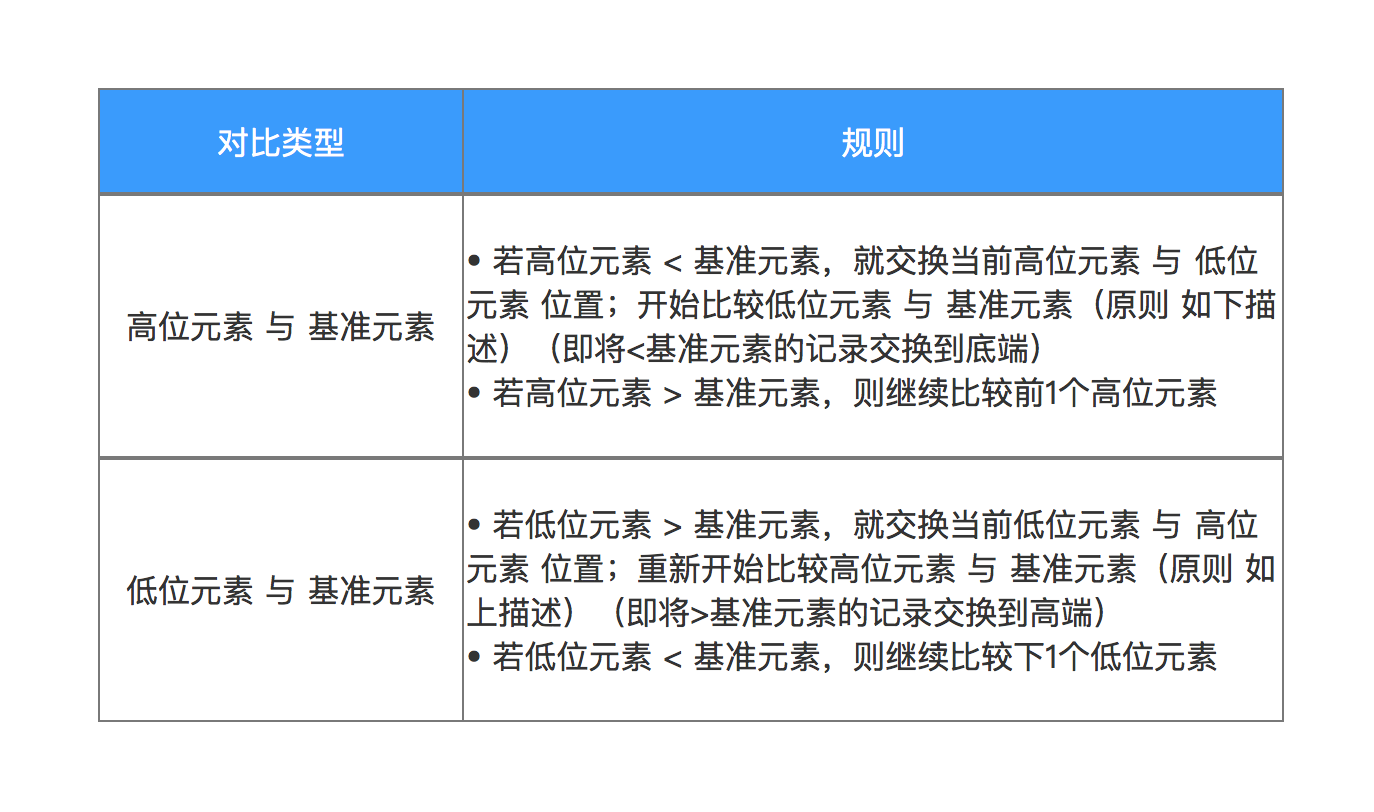
b. 分别对比 高位元素、低位元素 与 基准元素，具体规则如下：

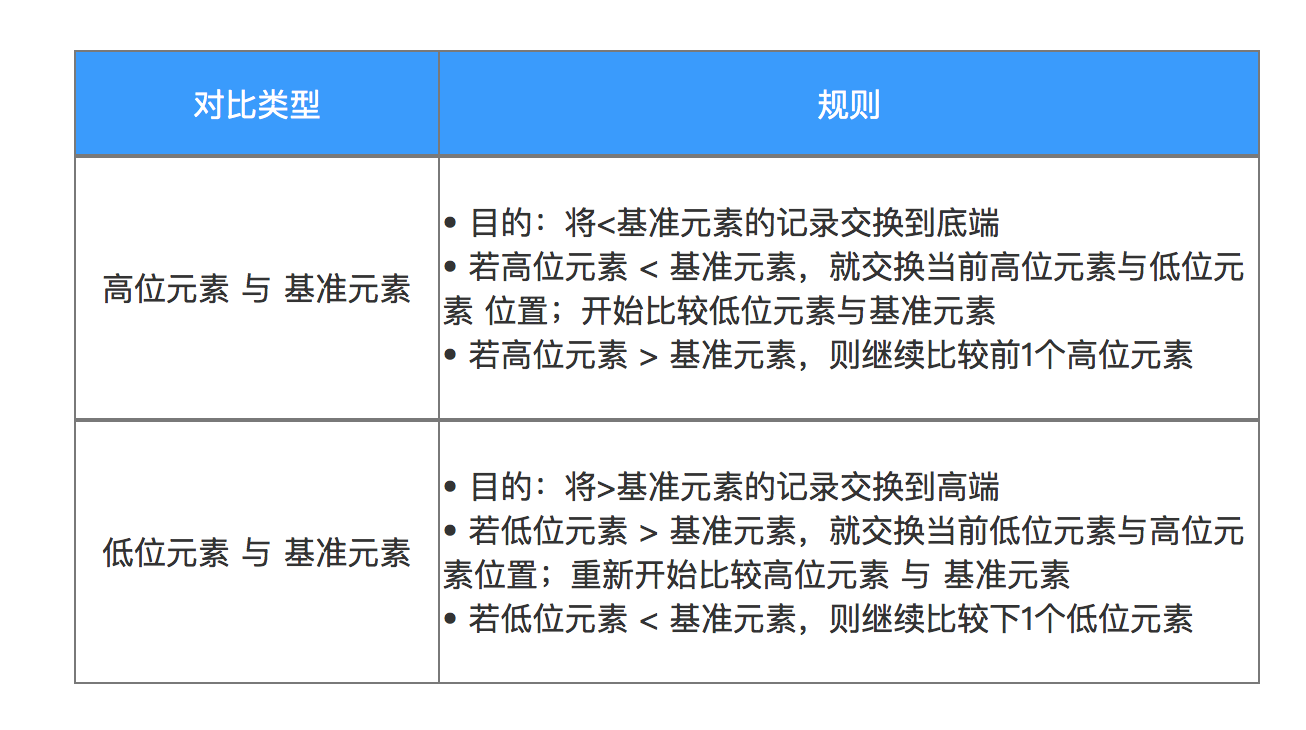
具体对比过程如下：

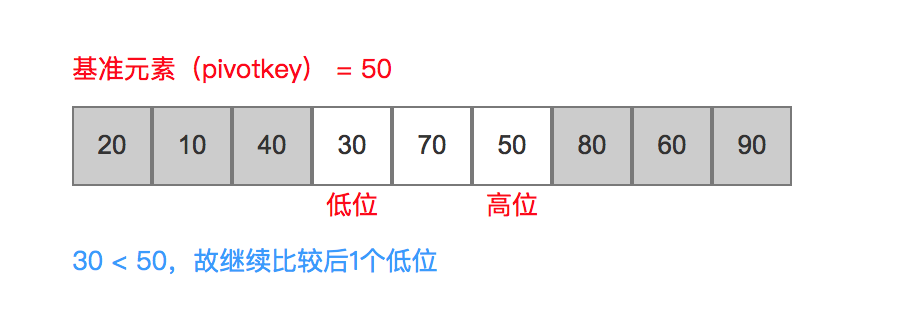
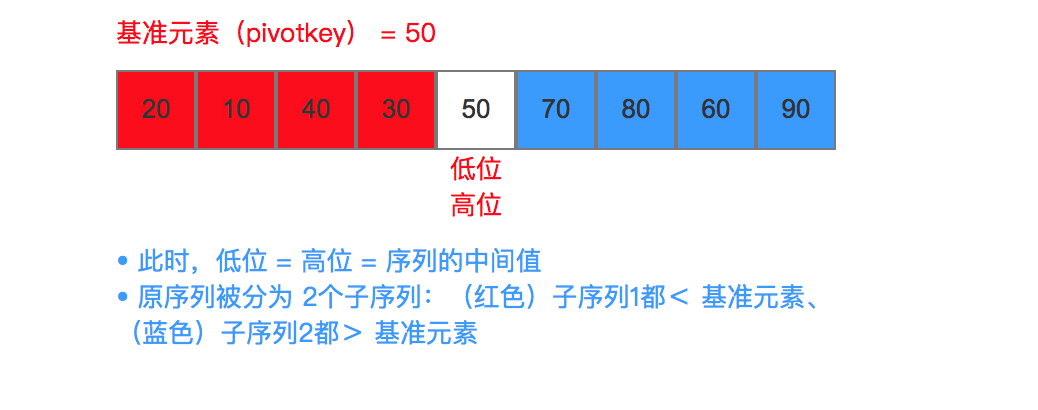
步骤2：分别对这2个子序列 进行排序

---

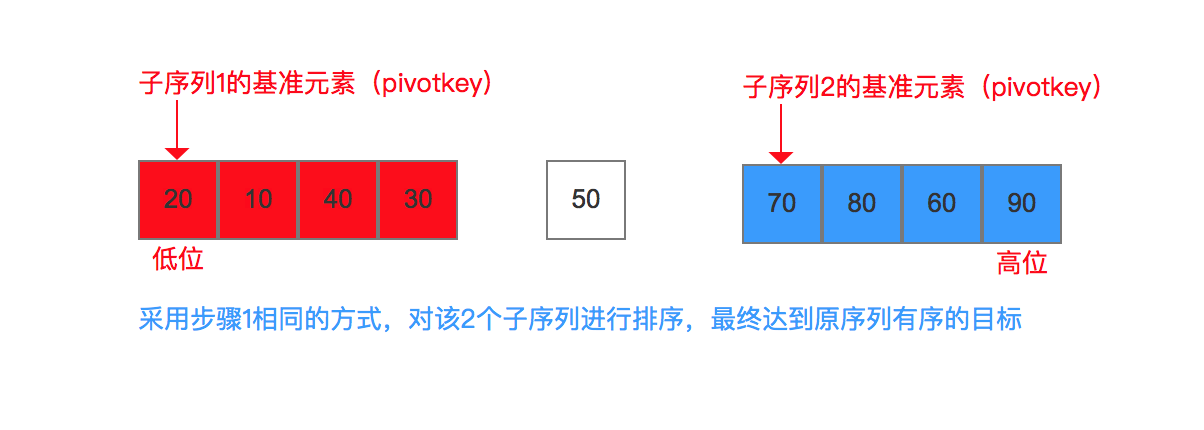
4. 算法实现

4.1 快速排序算法实现（基础实现）

• 步骤1：通过分区函数Partition（）将序列分割成2个独立子序列（高、低）
• 步骤2：对上述2个子序列使用快速排序方法进行递归

public class QuickSort {/*** 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {if (low < high) {// 1. 将待排序列 根据所选的枢纽位置，分割成独立的2个子序列// 最终返回的是枢纽位置int privot = Partition(srcArray, low, high);// 2. 分别对这2个子序列 进行排序// a. 通过递归 对低字表进行排序quickSort(srcArray, low, privot - 1);// b. 通过递归 对高字表进行排序quickSort(srcArray, privot + 1, high);}}

分区函数Partition（）对于快速排序算法来说非常重要，下面将详细讲解

4.2 分区函数Partition（）

• 作用：将待排序列 根据所选的枢纽位置，分割成独立的2个子序列（基础实现）
• 返回值：所选的枢纽位置
• 原理：根据下面的规则比较高/低位元素与枢纽元素的区别。

    /*** 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {// 1. 将子表的第1个个记录作为枢纽int tmp = srcArray[low];while (low < high) {// 2. 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;// 3. 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}int temp1 = srcArray[high];srcArray[high] = srcArray[low];srcArray[low] = temp1;}// 4. 最终低位、高位都会指向枢纽位置，返回return low;}

4.3 执行 快速排序

    /*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

测试结果

10
20
30
40
50
60
70
80
90

• Demo地址
  Carson_Ho的Github地址：快速排序

---

5. 算法优化

• 算法优化概述

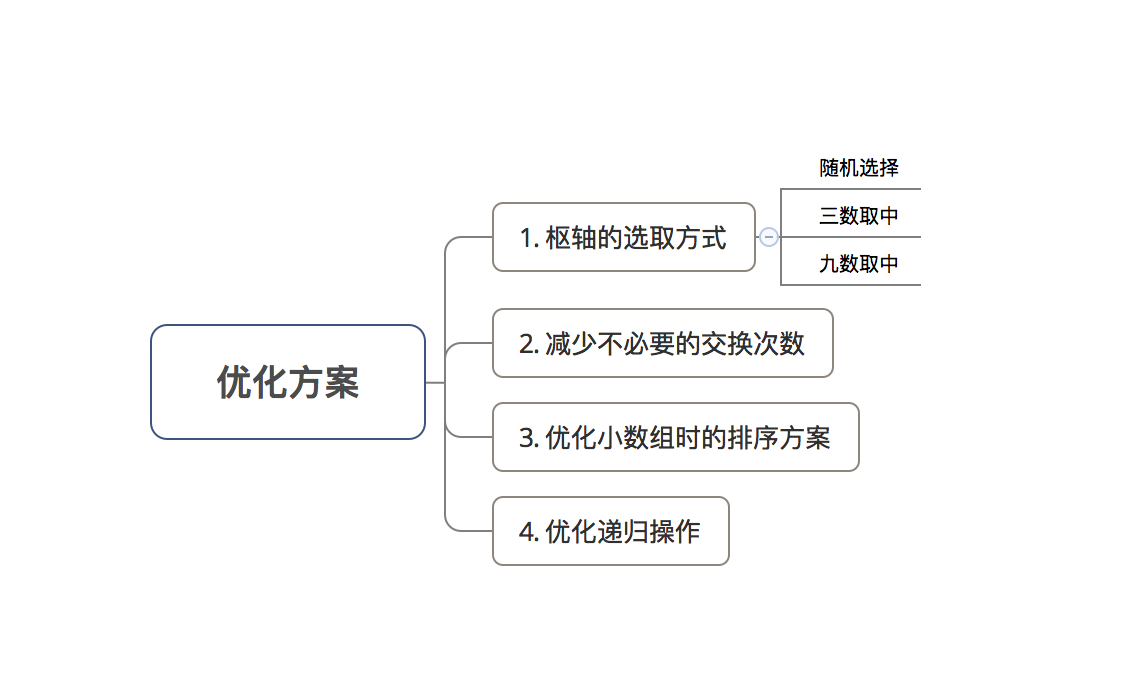
• 下面，我将详细讲解具体的优化方案

5.1 枢轴的选取方式

• 优化原因

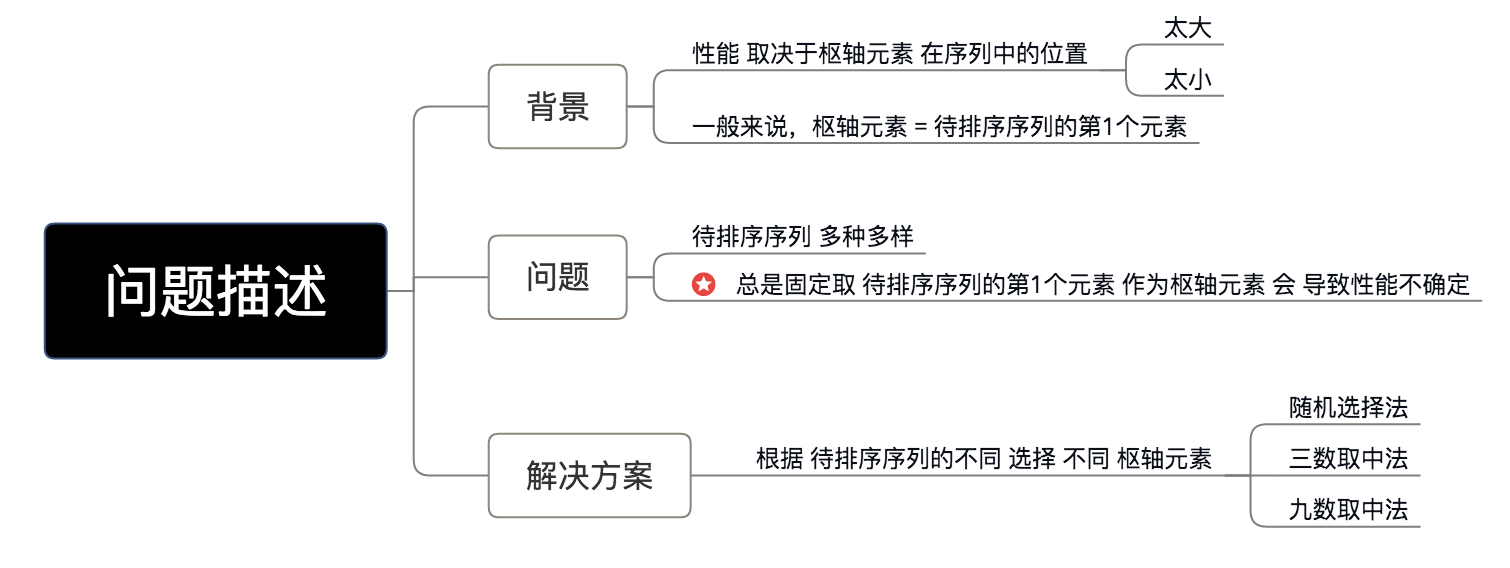
• 解决方案描述

下面，将演示 三数取中法 的代码实现。

主要修改处：在分区函数Partition（）中将枢纽的选择方式改为三数取中，具体原理是：

1. 找出中间元素
2. 比较左、右端数据元素，保证左端较小（若左>右，就交换位置）
3. 比较中、右端数据元素，保证中端较小（若中>右，就交换位置）
4. 比较中、左端数据元素，保证中端较小（若中>左，就交换位置）

  /*** 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {/*** 三数取中的方式*/// 1. 找出中间元素// 不是使用(low+high)/2的原因：容易溢出// 右移1位 = 除以2，但右移的运算速度更快int m = low + ( (high-low)>>1 );// 2. 比较左、右端数据元素，保证左端较小// 若左>右，就交换位置if(srcArray[low]>srcArray[high]) {int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;}// 3. 比较中、右端数据元素，保证中端较小// 若中>右，就交换位置if(srcArray[m]>srcArray[high]) {int temp1 = srcArray[m];srcArray[m] = srcArray[high];srcArray[high] = temp1;}// 4. 比较中、左端数据元素，保证中端较小if(srcArray[m]>srcArray[low]) {// 若中>左，就交换位置int temp2 = srcArray[m];srcArray[m] = srcArray[low];srcArray[low] = temp2;}// 此时，最低位 = srcArray[low] = 三数的中间数（即 最低位、最高位 & 中间数的中间值）// 将上述值作为枢纽int tmp = srcArray[low];System.out.println("枢轴位置 =" + srcArray[low]);/*** 下面代码类似未优化前（即，基础实现）*/while (low < high) {// 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;// 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}int temp1 = srcArray[high];srcArray[high] = srcArray[low];srcArray[low] = temp1;}// 最终低位、高位都会指向枢纽位置，返回return low;}

完整实现

public class QuickSort {/*** 快速排序算法实现（基础实现）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {if (low < high) {// 1. 将待排序列 根据所选的枢纽位置，分割成独立的2个子序列// 最终返回的是枢纽位置（主要优化在取取枢纽值里）int privot = Partition(srcArray, low, high);// 2. 分别对这2个子序列 进行排序// a. 通过递归 对低字表进行排序quickSort(srcArray, low, privot - 1);// b. 通过递归 对高字表进行排序quickSort(srcArray, privot + 1, high);}}/*** 作用：将待排序列 根据所选的枢纽位置，分割成独立的2个子序列（优化 = 选取枢轴 = 三数取中）* 返回值：所选的枢纽位置* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {/*** 三数取中的方式*/// 1. 找出中间元素// 不是使用(low+high)/2的原因：容易溢出// 右移1位 = 除以2，但右移的运算速度更快int m = low + ( (high-low)>>1 );// 2. 比较左、右端数据元素，保证左端较小// 若左>右，就交换位置if(srcArray[low]>srcArray[high]) {int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;}// 3. 比较中、右端数据元素，保证中端较小// 若中>右，就交换位置if(srcArray[m]>srcArray[high]) {int temp1 = srcArray[m];srcArray[m] = srcArray[high];srcArray[high] = temp1;}// 4. 比较中、左端数据元素，保证中端较小if(srcArray[m]>srcArray[low]) {// 若中>左，就交换位置int temp2 = srcArray[m];srcArray[m] = srcArray[low];srcArray[low] = temp2;}// 此时，最低位 = srcArray[low] = 三数的中间数（即 最低位、最高位 & 中间数的中间值）// 将上述值作为枢纽int tmp = srcArray[low];System.out.println("枢轴位置 =" + srcArray[low]);/*** 下面代码类似未优化前（即，基础实现）*/while (low < high) {// 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;// 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}int temp1 = srcArray[high];srcArray[high] = srcArray[low];srcArray[low] = temp1;}// 最终低位、高位都会指向枢纽位置，返回return low;}/*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

测试结果

枢轴位置 =50
枢轴位置 =30
枢轴位置 =10
枢轴位置 =80
枢轴位置 =60
10
20
30
40
50
60
70
80
90

5.2 减少不必要的交换

• 问题描述

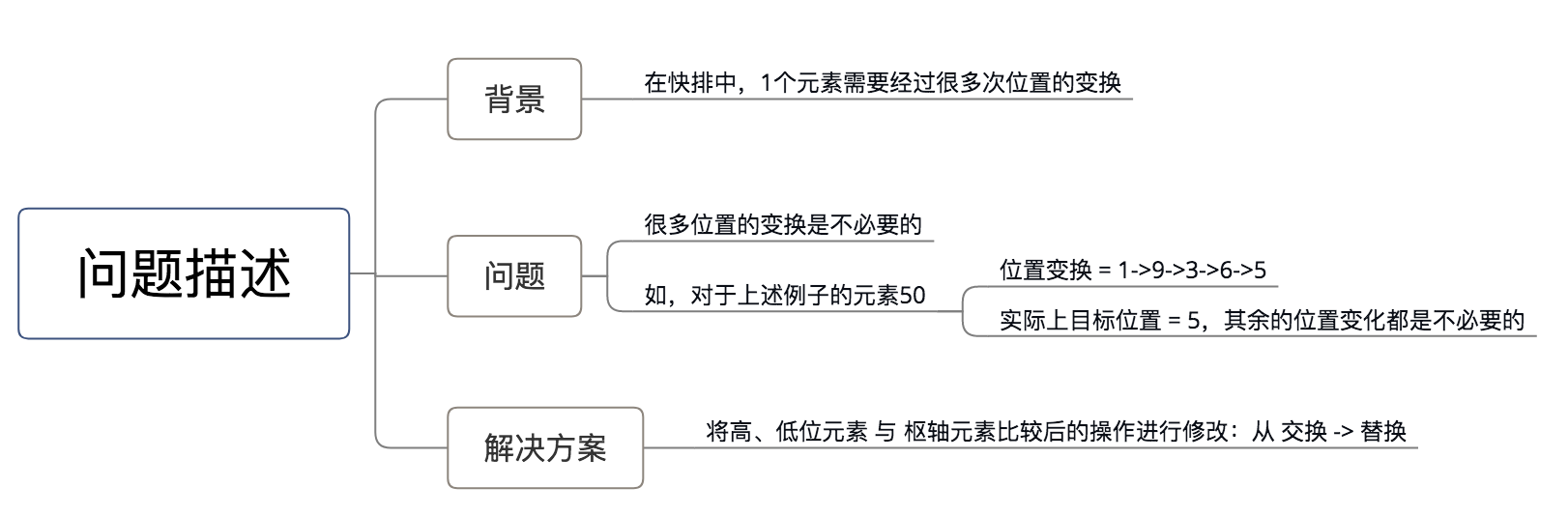
• 解决方案
  将高、低位元素 与 枢轴元素比较后的操作进行修改：从 交换 -> 替换，具体请看下列代码演示

主要修改点时在分区函数Partition（）中

   /*** 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {// 1. 将子表的第1个个记录作为枢纽int tmp = srcArray[low];while (low < high) {// 2. 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}// 采用 替换操作 换掉之前的 交换操作srcArray[low] = srcArray[high];// 之前的交换操作// int temp = srcArray[low];// srcArray[low] = srcArray[high];// srcArray[high] = temp;// 3. 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}// 采用 替换操作 换掉之前的 交换操作srcArray[high] = srcArray[low];// 之前的交换操作// int temp1 = srcArray[high];// srcArray[high] = srcArray[low];// srcArray[low] = temp1;}// 将枢轴元素替换到当前低位指针指向的元素 & 返回srcArray[low] = tmp;return low;}

完整实现

public class QuickSort {/*** 快速排序算法实现（优化 = 减少不必要的交换）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {if (low < high) {// 1. 将待排序列 根据所选的枢纽位置，分割成独立的2个子序列// 最终返回的是枢纽位置（主要优化在取枢纽值里）int privot = Partition(srcArray, low, high);// 2. 分别对这2个子序列 进行排序// a. 通过递归 对低字表进行排序quickSort(srcArray, low, privot - 1);// b. 通过递归 对高字表进行排序quickSort(srcArray, privot + 1, high);}}/*** 作用：将待排序列 根据所选的枢纽位置，分割成独立的2个子序列（优化 = 减少不必要的交换）* 返回值：所选的枢纽位置* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {// 1. 将子表的第1个个记录作为枢纽int tmp = srcArray[low];while (low < high) {// 2. 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}// 采用 替换操作 换掉之前的 交换操作srcArray[low] = srcArray[high];// 之前的交换操作// int temp = srcArray[low];// srcArray[low] = srcArray[high];// srcArray[high] = temp;// 3. 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}// 采用 替换操作 换掉之前的 交换操作srcArray[high] = srcArray[low];// 之前的交换操作// int temp1 = srcArray[high];// srcArray[high] = srcArray[low];// srcArray[low] = temp1;}// 将枢轴元素替换到当前低位指针指向的元素 & 返回srcArray[low] = tmp;return low;}/*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

• 测试结果

10
20
30
40
50
60
70
80
90

5.3 优化数据量较小序列的排序方案

• 问题描述

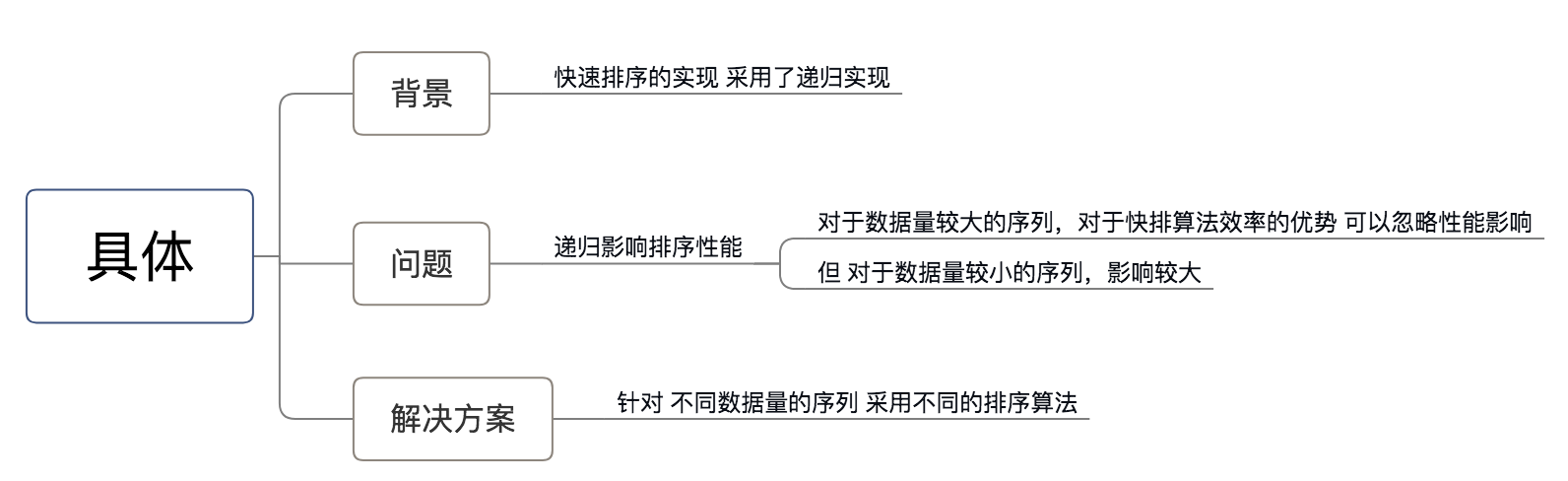
• 解决方案
  1. 对于数据量较大的序列：采用快速排序

资料显示，当序列的数据量>7时，视为大数据量序列

2. 对于数据量较小的序列：采用 直接插入排序

a. 直接插入排序是简单排序算法中性能最好的
b. 优化主要在quickSort（）中

• 具体实现

public class QuickSort {/*** 快速排序算法实现（优化 = 优化数据量较小序列的排序方案）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {// 当序列的数据量>7时，视为大数据量序列，此时采用 快速排序if (high-low > 7) {if (low < high) {System.out.println("采用快排");int privot = Partition(srcArray, low, high);quickSort(srcArray, low, privot - 1);quickSort(srcArray, privot + 1, high);}}else{// 当序列的数据量<7时，视为小数据量序列，此时采用 直接插入排序insertSort(srcArray);System.out.println("采用直接插入排序");};}/*** 作用：将待排序列 根据所选的枢纽位置，分割成独立的2个子序列（优化 = 优化数据量较小序列的排序方案）* 返回值：所选的枢纽位置* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {// 1. 将子表的第1个个记录作为枢纽int tmp = srcArray[low];while (low < high) {// 2. 比较高位元素 & 枢纽元素// 若高位元素 > 枢纽元素，则继续比较前1个高位元素// 若高位元素 < 枢纽元素，则交换当前高位元素 与 低位元素 位置、开始比较低位元素 与 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;// 3. 比较低位元素 & 枢纽元素// 若低位元素 < 基准元素，则继续比较下1个低位元素// 若低位元素 > 枢纽元素，就交换当前低位元素 与 高位元素 位置；重新开始比较高位元素 与 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}int temp1 = srcArray[high];srcArray[high] = srcArray[low];srcArray[low] = temp1;}// 最终低位、高位都会指向枢纽位置，返回return low;}/*** 直接插入排序 算法实现*/public static void insertSort(int[] srcArray) {int i; // 用于存放当前插入数据记录的数组下标int j; // 用于存放需要比较记录的下标int temp; // 用于交换数据// 从第1个数据记录 开始，该元素可以认为已经被排序for(i = 0 ; i < srcArray.length ; i++){temp = srcArray[i];// 取出下一个数据记录，在已经排序的序列中从后向前扫描// 将 当前数据记录 与 前面排序好的值进行比较for(j = i ; j > 0 && temp < srcArray[j-1] ; j --){// 按照顺序小 -> 大 将 当前需要插入的数据记录插入到合适位置 = 后移已排序好的元素 + 插入新的数据记录// a. 后移已排序好的元素srcArray[j] = srcArray[j-1];}// 插入新的数据记录srcArray[j] = temp;}}/*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

注：关于直接插入排序算法实现可自行了解。

• 测试结果

采用快排
采用直接插入排序
采用直接插入排序
10
20
30
40
50
60
70
80
90

特别注意：此处的排序方式选择不只是第一次排序，而是贯穿 整个快速排序过程，即 由于快速排序过程 = 逐步划分成半子表的过程，所以最后几次的排序一定会使用 直接插入排序

5.4 优化递归操作

• 问题描述

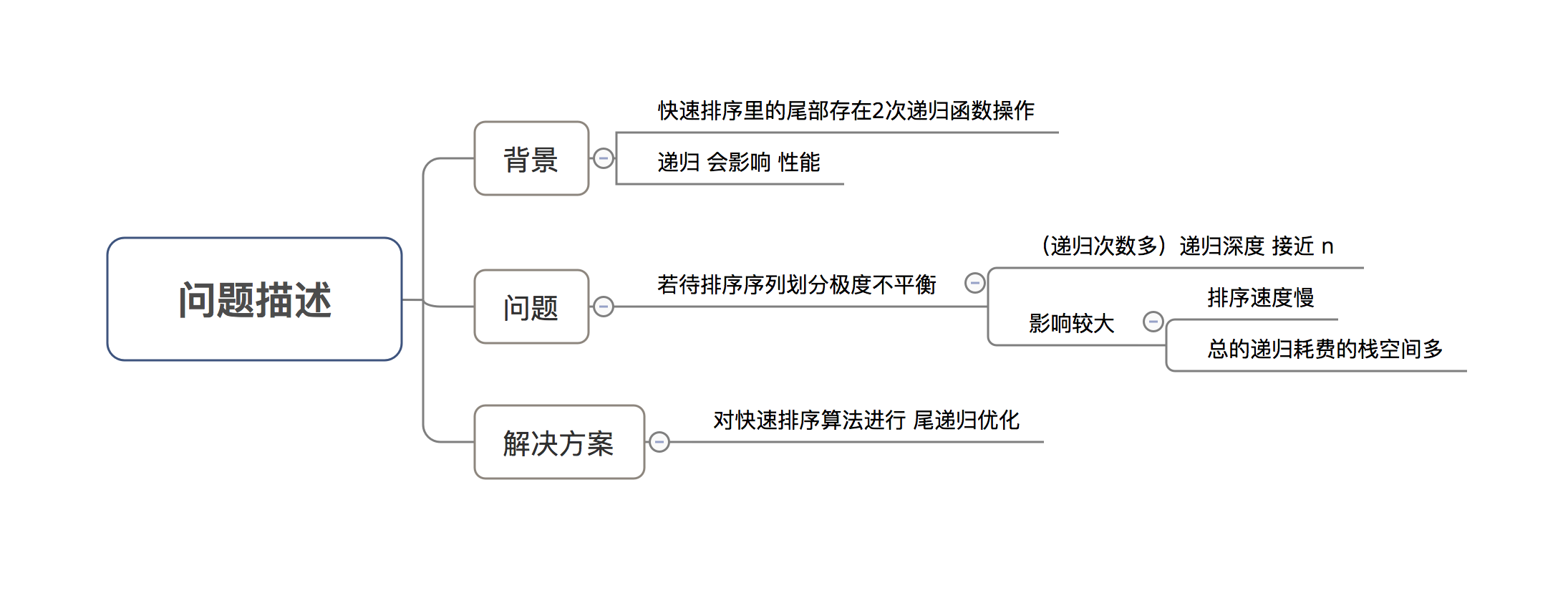
• 解决方案实现
  将快速排序算法最后的 尾部递归操作 改成 迭代操作

1. 可有效缩减所需的堆栈深度，从而有效提高性能
2. 主要在主要算法的quickSort（）中

public class QuickSort {/*** 快速排序算法实现（优化 = 优化递归 = 采用 迭代操作 代替 递归操作）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {// 将if 改成 While，原来操作为：if (low < high)while (low < high) {int privot = Partition(srcArray, low, high);quickSort(srcArray, low, privot - 1);low = privot +1 ;// 将 尾递归中对高字表的排序 改成 low = privot +1，原来操作为：quickSort(srcArray, privot + 1, high);// 原因：在第1次循环后，后1次循环中的Partition(srcArray, low, high) = quickSort(srcArray, privot + 1, high)// 故可删去该递归}}/*** 作用：将待排序列 根据所选的枢纽位置，分割成独立的2个子序列（优化 = 优化递归 = 采用 迭代操作 代替 递归操作）* 返回值：所选的枢纽位置* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {// 1. 将子表的第1个个记录作为枢纽int tmp = srcArray[low];while (low < high) {// 2. 比较高位元素 & 枢纽元素while (low < high && srcArray[high] >= tmp) {high--;}int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;// 3. 比较低位元素 & 枢纽元素while (low < high && srcArray[low] <= tmp) {low++;}int temp1 = srcArray[high];srcArray[high] = srcArray[low];srcArray[low] = temp1;}// 最终低位、高位都会指向枢纽位置，返回return low;}/*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

• 测试结果

10
20
30
40
50
60
70
80
90

5.5 总结

最终，总结4种优化方式 & 贴出最终优化后的快速排序算法

• 方案总结

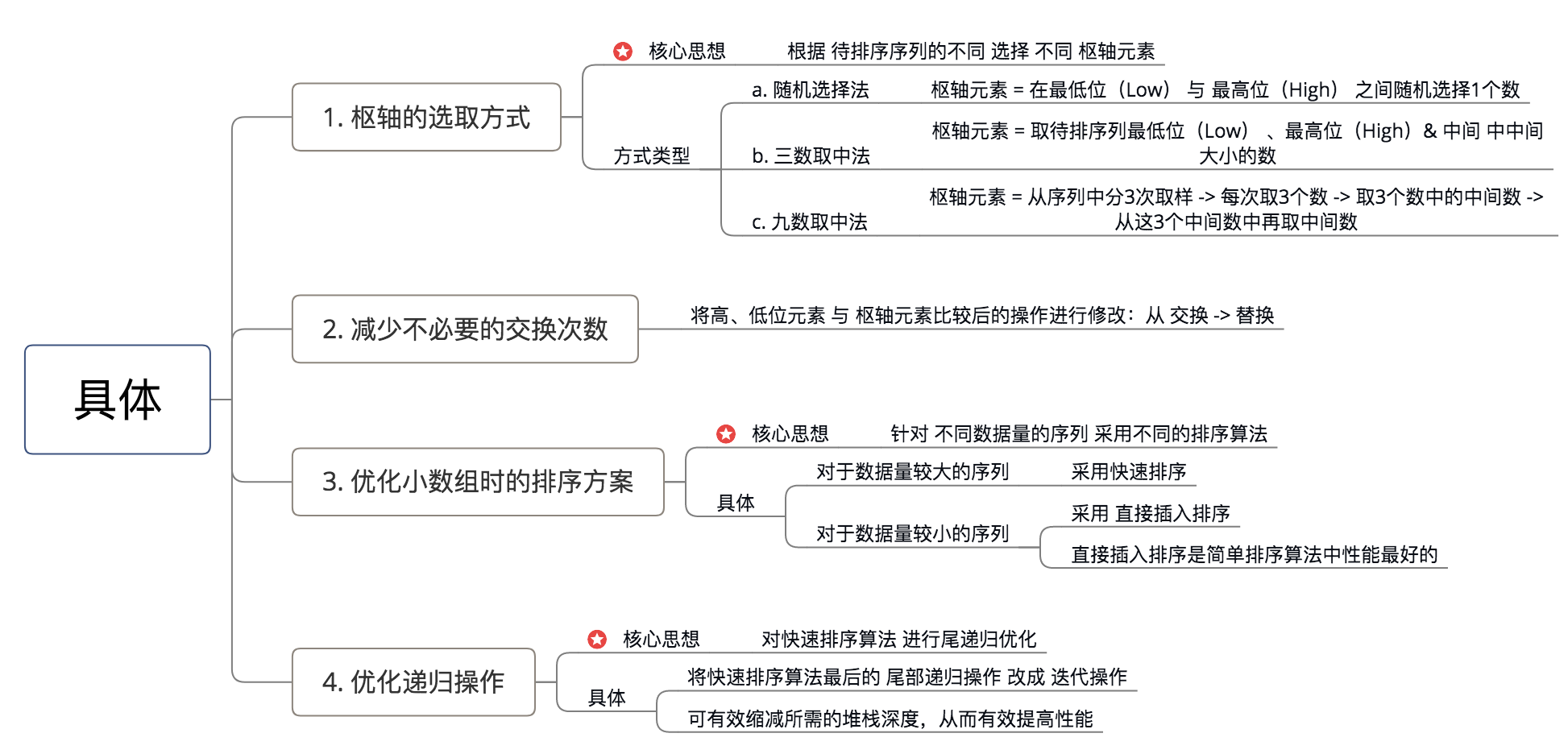
• 具体代码

public class QuickSort {/*** 快速排序算法实现（优化 = 选取枢轴、减少不必要的交换次数、优化数据量较小序列的排序方案、将尾递归操作->迭代操作）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static void quickSort(int[] srcArray, int low, int high) {/*** 优化3：优化数据量较小序列的排序方案 = 步骤8、9*/if (high-low > 7) {// 8. 当序列的数据量>7时，视为大数据量序列，此时采用 快速排序System.out.println("采用快排");/*** 优化4：将尾递归操作->迭代操作 = 步骤10、11*/// 10. 将if 改成 While，原来操作为：if (low < high)while (low < high) {int privot = Partition(srcArray, low, high);quickSort(srcArray, low, privot - 1);// 11. // 将 尾递归中对高字表的排序 改成 low = privot +1，原来操作为：quickSort(srcArray, privot + 1, high);// quickSort_RecursionOp(srcArray, middle + 1, high);low = privot +1 ;}}else{// 9. 当序列的数据量<7时，视为小数据量序列，此时采用 直接插入排序insertSort(srcArray);System.out.println("采用直接插入排序");}}/*** 快速排序算法中寻找中间元素 实现（优化 = 选取枢轴、减少不必要的交换次数、优化数据量较小序列的排序方案、将尾递归操作->迭代操作）* 参数说明：* @param srcArray = 需排序的数组序列* @param low = 数组第1个元素下标* @param high = 数组最后1个元素下标*/public static int Partition(int[] srcArray, int low, int high) {/*** 优化1：三数取中选取枢轴 = 步骤1、2、3、4、5*/// 1. 找出中间元素int m = low + (high - low) /2;// 2. 比较左、右端数据元素，保证左端较小// 若左>右，就交换位置if(srcArray[low]>srcArray[high]) {int temp = srcArray[low];srcArray[low] = srcArray[high];srcArray[high] = temp;}// 3. 比较中、右端数据元素，保证中端较小// 若中>右，就交换位置if(srcArray[m]>srcArray[high]) {int temp1 = srcArray[m];srcArray[m] = srcArray[high];srcArray[high] = temp1;}// 4. 比较中、左端数据元素，保证中端较小if(srcArray[m]>srcArray[low]) {// 若中>左，就交换位置int temp2 = srcArray[m];srcArray[m] = srcArray[low];srcArray[low] = temp2;}// 此时，最低位 = srcArray[low] = 三数的中间数（即 最低位、最高位 & 中间数的中间值）// 将上述值作为枢纽int tmp = srcArray[low];System.out.println("枢轴位置 =" + srcArray[low]);/*** 优化2：减少不必要的交换次数 = 步骤5.6.7*/while (low < high) {while (low < high && srcArray[high] >= tmp) {high--;}// 5. 采用 替换操作 换掉之前的 交换操作srcArray[low] = srcArray[high];// 之前的交换操作// int temp = srcArray[low];// srcArray[low] = srcArray[high];// srcArray[high] = temp;while (low < high && srcArray[low] <= tmp) {low++;}// 6. 采用 替换操作 换掉之前的 交换操作srcArray[high] = srcArray[low];// 之前的交换操作// int temp1 = srcArray[high];// srcArray[high] = srcArray[low];// srcArray[low] = temp1;}// 7. 将枢轴元素替换到当前低位指针指向的元素 & 返回srcArray[low] = tmp;return low;}/*** 直接插入排序 算法实现*/public static void insertSort(int[] srcArray) {int i; // 用于存放当前插入数据记录的数组下标int j; // 用于存放需要比较记录的下标int temp; // 用于交换数据// 从第1个数据记录 开始，该元素可以认为已经被排序for(i = 0 ; i < srcArray.length ; i++){temp = srcArray[i];// 取出下一个数据记录，在已经排序的序列中从后向前扫描// 将 当前数据记录 与 前面排序好的值进行比较for(j = i ; j > 0 && temp < srcArray[j-1] ; j --){// 按照顺序小 -> 大 将 当前需要插入的数据记录插入到合适位置 = 后移已排序好的元素 + 插入新的数据记录// a. 后移已排序好的元素srcArray[j] = srcArray[j-1];}// 插入新的数据记录srcArray[j] = temp;}}/*** 执行 快速排序*/public static void main(String[] args) {// 定义待排序数列int[] src = new int[]{ 50, 10, 90, 30, 70, 40, 80, 60, 20 };// 输出结果quickSort(src,0,src.length-1);// 输出 排序后的序列for (int a = 0; a < src.length; a++) {System.out.println(src[a]);}}
}

• 测试结果

枢轴位置 =50
采用直接插入排序
枢轴位置 =70
采用直接插入排序
枢轴位置 =80
采用直接插入排序
10
20
30
40
50
60
70
80
90

---

6. 性能分析

以下将分析算法的性能：时间复杂度、空间复杂度、稳定性

---

总结

• 本文对 全面讲解了快速排序
• 接下来推出的文章，我将继续讲解数据结构的相关知识，感兴趣的读者可以继续关注我的博客哦：Carson_Ho的Android博客

---

请帮顶 / 评论点赞！因为你们的赞同/鼓励是我写作的最大动力！