本文主要是介绍曲率、曲率圆和曲率半径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
一个圆半径越小，看起来就越弯曲；半径越大，看起来就越平；半径无限大，看起来就像一条直线，几乎不弯曲了。 —— 引言
曲率是描述曲线弯曲程度的量。从上面左图可以看出，弯曲程度越大、转角越大；从右图可以看出，转角相同时，弧越短、弯曲程度越大。
如上图所示，曲线C在M点的曲率定义为：
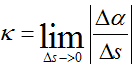
如上图所示，设曲线y=f(x)在点M处的曲率为
，在点M处的曲线的法线上，在凹的一侧取一点D，使得：
以D为圆心、
为半径画圆，称此圆为曲线在点M处的曲率圆。D为曲率中心，
为曲率半径。
根据以上分析，圆上所有点的曲率相等，都等于其半径的倒数。
这篇关于曲率、曲率圆和曲率半径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
