C++标准模板（STL）- 类型支持 (数值极限，max_digits10，radix，min_exponent)

本文主要是介绍C++标准模板（STL）- 类型支持 (数值极限，max_digits10，radix，min_exponent)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数值极限

定义于头文件 <limits>

定义于头文件 <limits>
template< class T > class numeric_limits;

numeric_limits 类模板提供查询各种算术类型属性的标准化方式（例如 int 类型的最大可能值是 std::numeric_limits<int>::max() ）。
 

区别所有此类型值所需的十进制位数

std::numeric_limits<T>::max_digits10

static constexpr int max_digits10

(C++11 起)

 std::numeric_limits<T>::max_digits10 的值是唯一地表示所有类型 T 值的底 10 位数，是为序列化/反序列化到文本所需。此常量对所有浮点类型有意义。

标准特化

T	std::numeric_limits<T>::max_digits10 的值
/* non-specialized */	​0​
bool	​0​
char	​0​
signed char	​0​
unsigned char	​0​
wchar_t	​0​
char8_t	​0​
char16_t	​0​
char32_t	​0​
short	​0​
unsigned short	​0​
int	​0​
unsigned int	​0​
long	​0​
unsigned long	​0​
long long	​0​
unsigned long long	​0​
float	FLT_DECIMAL_DIG 或 std::ceil(std::numeric_limits<float>::digits * std::log10(2) + 1)
double	DBL_DECIMAL_DIG 或 std::ceil(std::numeric_limits<double>::digits * std::log10(2) + 1)
long double	DECIMAL_DIG 或 LDBL_DECIMAL_DIG 或 std::ceil(std::numeric_limits<long double>::digits * std::log10(2) + 1)

注意

不同于多数数学运算，只要用至少 max_digits10 （对于 float 为 9 ，对于 double 为 17 ）位，则从浮点值转换到文本并转换回来是准确的：保证产生同一浮点值，即使不确定的文本表示不准确。以小数点记法，可能需要超过一百个十进制小数位表示 float 的精确值。

调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>struct SName
{
};//偏特化
struct SPartSpec
{
};namespace std
{
template<>
struct numeric_limits<SPartSpec>
{static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;
};
}int main()
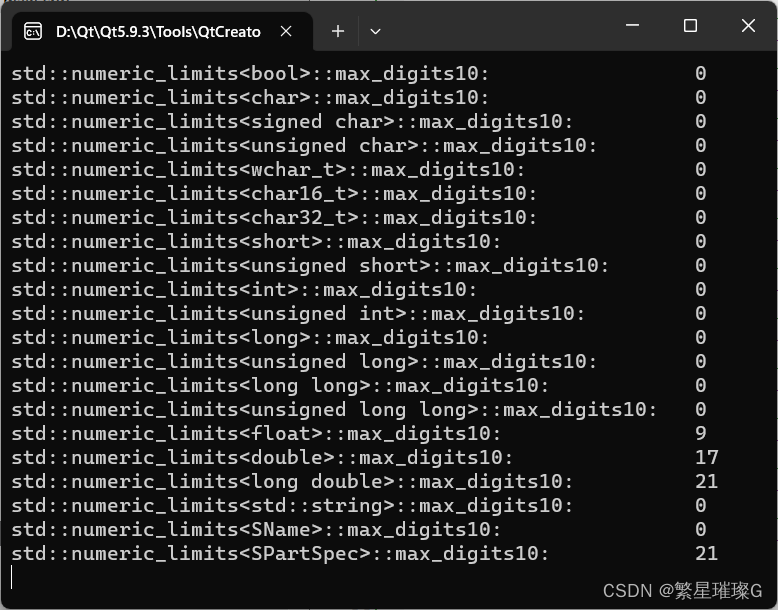
{std::cout << std::boolalpha;std::cout << "std::numeric_limits<bool>::max_digits10:                 "<< std::numeric_limits<bool>::max_digits10 << std::endl;std::cout << "std::numeric_limits<char>::max_digits10:                 "<< std::numeric_limits<char>::max_digits10 << std::endl;std::cout << "std::numeric_limits<signed char>::max_digits10:          "<< std::numeric_limits<signed char>::max_digits10 << std::endl;std::cout << "std::numeric_limits<unsigned char>::max_digits10:        "<< std::numeric_limits<unsigned char>::max_digits10 << std::endl;std::cout << "std::numeric_limits<wchar_t>::max_digits10:              "<< std::numeric_limits<wchar_t>::max_digits10 << std::endl;std::cout << "std::numeric_limits<char16_t>::max_digits10:             "<< std::numeric_limits<char16_t>::max_digits10 << std::endl;std::cout << "std::numeric_limits<char32_t>::max_digits10:             "<< std::numeric_limits<char32_t>::max_digits10 << std::endl;std::cout << "std::numeric_limits<short>::max_digits10:                "<< std::numeric_limits<short>::max_digits10 << std::endl;std::cout << "std::numeric_limits<unsigned short>::max_digits10:       "<< std::numeric_limits<unsigned short>::max_digits10 << std::endl;std::cout << "std::numeric_limits<int>::max_digits10:                  "<< std::numeric_limits<int>::max_digits10 << std::endl;std::cout << "std::numeric_limits<unsigned int>::max_digits10:         "<< std::numeric_limits<unsigned int>::max_digits10 << std::endl;std::cout << "std::numeric_limits<long>::max_digits10:                 "<< std::numeric_limits<long>::max_digits10 << std::endl;std::cout << "std::numeric_limits<unsigned long>::max_digits10:        "<< std::numeric_limits<unsigned long>::max_digits10 << std::endl;std::cout << "std::numeric_limits<long long>::max_digits10:            "<< std::numeric_limits<long long>::max_digits10 << std::endl;std::cout << "std::numeric_limits<unsigned long long>::max_digits10:   "<< std::numeric_limits<unsigned long long>::max_digits10 << std::endl;std::cout << "std::numeric_limits<float>::max_digits10:                "<< std::numeric_limits<float>::max_digits10 << std::endl;std::cout << "std::numeric_limits<double>::max_digits10:               "<< std::numeric_limits<double>::max_digits10 << std::endl;std::cout << "std::numeric_limits<long double>::max_digits10:          "<< std::numeric_limits<long double>::max_digits10 << std::endl;std::cout << "std::numeric_limits<std::string>::max_digits10:          "<< std::numeric_limits<std::string>::max_digits10 << std::endl;std::cout << "std::numeric_limits<SName>::max_digits10:                "<< std::numeric_limits<SName>::max_digits10 << std::endl;std::cout << "std::numeric_limits<SPartSpec>::max_digits10:            "<< std::numeric_limits<SPartSpec>::max_digits10 << std::endl;return 0;
}

输出

给定类型的表示所用的基或整数底

std::numeric_limits<T>::radix

static const int radix;		(C++11 前)
static constexpr int radix;		(C++11 起)

 std::numeric_limits<T>::radix 的值是用于表示该类型的数字系统的底。对于所有二进制数值类型为 2 ，但它可以，譬如对 IEEE 754 十进制浮点类型或第三方二进制编码十进制整数为 10 。此常量对所有特化有意义。

标准特化

T	std::numeric_limits<T>::radix 的值
/* non-specialized */	​0​
bool	2
char	2
signed char	2
unsigned char	2
wchar_t	2
char8_t	2
char16_t	2
char32_t	2
short	2
unsigned short	2
int	2
unsigned int	2
long	2
unsigned long	2
long long	2
unsigned long long	2
float	FLT_RADIX
double	FLT_RADIX
long double	FLT_RADIX

调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>struct SName
{
};//偏特化
struct SPartSpec
{
};namespace std
{
template<>
struct numeric_limits<SPartSpec>
{static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;
};
}int main()
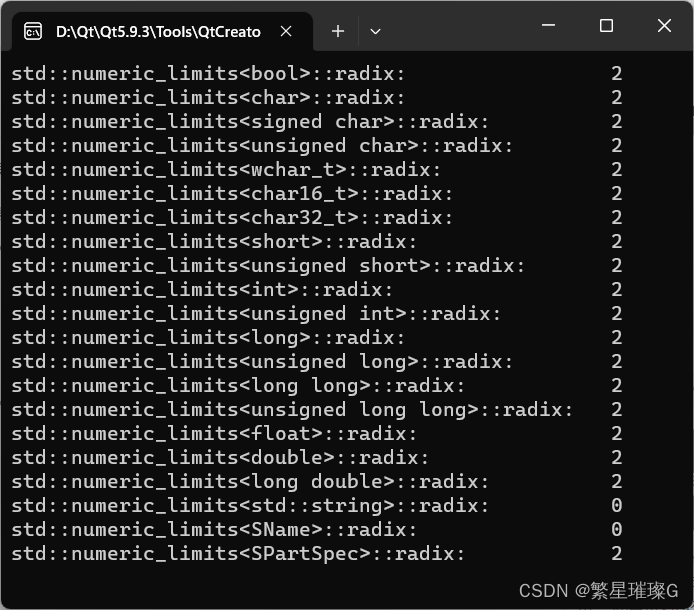
{std::cout << std::boolalpha;std::cout << "std::numeric_limits<bool>::radix:                 "<< std::numeric_limits<bool>::radix << std::endl;std::cout << "std::numeric_limits<char>::radix:                 "<< std::numeric_limits<char>::radix << std::endl;std::cout << "std::numeric_limits<signed char>::radix:          "<< std::numeric_limits<signed char>::radix << std::endl;std::cout << "std::numeric_limits<unsigned char>::radix:        "<< std::numeric_limits<unsigned char>::radix << std::endl;std::cout << "std::numeric_limits<wchar_t>::radix:              "<< std::numeric_limits<wchar_t>::radix << std::endl;std::cout << "std::numeric_limits<char16_t>::radix:             "<< std::numeric_limits<char16_t>::radix << std::endl;std::cout << "std::numeric_limits<char32_t>::radix:             "<< std::numeric_limits<char32_t>::radix << std::endl;std::cout << "std::numeric_limits<short>::radix:                "<< std::numeric_limits<short>::radix << std::endl;std::cout << "std::numeric_limits<unsigned short>::radix:       "<< std::numeric_limits<unsigned short>::radix << std::endl;std::cout << "std::numeric_limits<int>::radix:                  "<< std::numeric_limits<int>::radix << std::endl;std::cout << "std::numeric_limits<unsigned int>::radix:         "<< std::numeric_limits<unsigned int>::radix << std::endl;std::cout << "std::numeric_limits<long>::radix:                 "<< std::numeric_limits<long>::radix << std::endl;std::cout << "std::numeric_limits<unsigned long>::radix:        "<< std::numeric_limits<unsigned long>::radix << std::endl;std::cout << "std::numeric_limits<long long>::radix:            "<< std::numeric_limits<long long>::radix << std::endl;std::cout << "std::numeric_limits<unsigned long long>::radix:   "<< std::numeric_limits<unsigned long long>::radix << std::endl;std::cout << "std::numeric_limits<float>::radix:                "<< std::numeric_limits<float>::radix << std::endl;std::cout << "std::numeric_limits<double>::radix:               "<< std::numeric_limits<double>::radix << std::endl;std::cout << "std::numeric_limits<long double>::radix:          "<< std::numeric_limits<long double>::radix << std::endl;std::cout << "std::numeric_limits<std::string>::radix:          "<< std::numeric_limits<std::string>::radix << std::endl;std::cout << "std::numeric_limits<SName>::radix:                "<< std::numeric_limits<SName>::radix << std::endl;std::cout << "std::numeric_limits<SPartSpec>::radix:            "<< std::numeric_limits<SPartSpec>::radix << std::endl;return 0;
}

输出

 底的该数次幂是合法正规浮点值的最小负数加一

std::numeric_limits<T>::min_exponent

static const int min_exponent;		(C++11 前)
static constexpr int min_exponent;		(C++11 起)

标准特化

T	std::numeric_limits<T>::min_exponent 的值
/* non-specialized */	​0​
bool	​0​
char	​0​
signed char	​0​
unsigned char	​0​
wchar_t	​0​
char8_t	​0​
char16_t	​0​
char32_t	​0​
short	​0​
unsigned short	​0​
int	​0​
unsigned int	​0​
long	​0​
unsigned long	​0​
long long	​0​
unsigned long long	​0​
float	FLT_MIN_EXP
double	DBL_MIN_EXP
long double	LDBL_MIN_EXP

调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>struct SName
{
};//偏特化
struct SPartSpec
{
};namespace std
{
template<>
struct numeric_limits<SPartSpec>
{static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;static _GLIBCXX_USE_CONSTEXPR int  min_exponent     = FLT_MIN_EXP;
};
}int main()
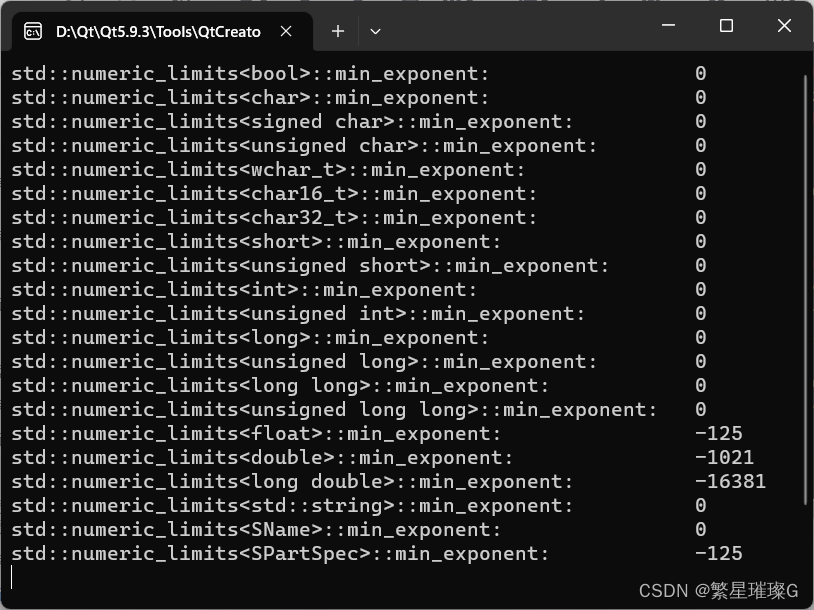
{std::cout << std::boolalpha;std::cout << "std::numeric_limits<bool>::min_exponent:                 "<< std::numeric_limits<bool>::min_exponent << std::endl;std::cout << "std::numeric_limits<char>::min_exponent:                 "<< std::numeric_limits<char>::min_exponent << std::endl;std::cout << "std::numeric_limits<signed char>::min_exponent:          "<< std::numeric_limits<signed char>::min_exponent << std::endl;std::cout << "std::numeric_limits<unsigned char>::min_exponent:        "<< std::numeric_limits<unsigned char>::min_exponent << std::endl;std::cout << "std::numeric_limits<wchar_t>::min_exponent:              "<< std::numeric_limits<wchar_t>::min_exponent << std::endl;std::cout << "std::numeric_limits<char16_t>::min_exponent:             "<< std::numeric_limits<char16_t>::min_exponent << std::endl;std::cout << "std::numeric_limits<char32_t>::min_exponent:             "<< std::numeric_limits<char32_t>::min_exponent << std::endl;std::cout << "std::numeric_limits<short>::min_exponent:                "<< std::numeric_limits<short>::min_exponent << std::endl;std::cout << "std::numeric_limits<unsigned short>::min_exponent:       "<< std::numeric_limits<unsigned short>::min_exponent << std::endl;std::cout << "std::numeric_limits<int>::min_exponent:                  "<< std::numeric_limits<int>::min_exponent << std::endl;std::cout << "std::numeric_limits<unsigned int>::min_exponent:         "<< std::numeric_limits<unsigned int>::min_exponent << std::endl;std::cout << "std::numeric_limits<long>::min_exponent:                 "<< std::numeric_limits<long>::min_exponent << std::endl;std::cout << "std::numeric_limits<unsigned long>::min_exponent:        "<< std::numeric_limits<unsigned long>::min_exponent << std::endl;std::cout << "std::numeric_limits<long long>::min_exponent:            "<< std::numeric_limits<long long>::min_exponent << std::endl;std::cout << "std::numeric_limits<unsigned long long>::min_exponent:   "<< std::numeric_limits<unsigned long long>::min_exponent << std::endl;std::cout << "std::numeric_limits<float>::min_exponent:                "<< std::numeric_limits<float>::min_exponent << std::endl;std::cout << "std::numeric_limits<double>::min_exponent:               "<< std::numeric_limits<double>::min_exponent << std::endl;std::cout << "std::numeric_limits<long double>::min_exponent:          "<< std::numeric_limits<long double>::min_exponent << std::endl;std::cout << "std::numeric_limits<std::string>::min_exponent:          "<< std::numeric_limits<std::string>::min_exponent << std::endl;std::cout << "std::numeric_limits<SName>::min_exponent:                "<< std::numeric_limits<SName>::min_exponent << std::endl;std::cout << "std::numeric_limits<SPartSpec>::min_exponent:            "<< std::numeric_limits<SPartSpec>::min_exponent << std::endl;return 0;
}

输出

这篇关于C++标准模板（STL）- 类型支持 (数值极限，max_digits10，radix，min_exponent)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---