参考HDU 4396完成 spfa算法及动态规划法的JAVA实现

为了实现一个最短路径问题的JAVA实现，参考杭电  HDU 4396题目进行JAVA改写

参考题目链接:   hdu 4396

 参考代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 5010
#define INF 0x3f3f3f3f
int Dp[MAX][505],pre[MAX],Index,visit[MAX][505];
struct snode{int to,w,next;
}Edge[210000];
struct node{int v,len;
}listb[2000000],v1,v2;void Add_edge(int a,int b,int c)
{Edge[Index].to=b; Edge[Index].w=c;Edge[Index].next=pre[a];pre[a]=Index++;
}int SPFA(int a,int b,int c)
{int s,e,i,vv,vlen;memset(visit,0,sizeof(visit));s=e=0;Dp[a][0]=0;v1.len=0,v1.v=a;listb[s++]=v1;while(s!=e){v1=listb[e++];visit[v1.v][v1.len]=0;for(i=pre[v1.v];i!=-1;i=Edge[i].next){vlen=v1.len+1;if(vlen>=c)    //把 len>K的看成Kvlen=c;vv=Edge[i].to;if(Dp[vv][vlen]>Dp[v1.v][v1.len]+Edge[i].w){Dp[vv][vlen]=Dp[v1.v][v1.len]+Edge[i].w;  //更新if(!visit[vv][vlen])  //防止重复人队列{v2.v=vv,v2.len=vlen;visit[vv][vlen]=1;listb[s++]=v2;}}}}return Dp[b][c];
}int main()
{int i,j,n,m,a,b,c,t;while(scanf("%d%d",&n,&m)!=EOF){Index=0;memset(pre,-1,sizeof(pre));memset(Dp,INF,sizeof(Dp));for(i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&c);Add_edge(a,b,c);Add_edge(b,a,c);}scanf("%d%d%d",&a,&b,&c);t=c;c/=10;if(t%10!=0)  c++;t=SPFA(a,b,c);if(t==INF)printf("-1\n");elseprintf("%d\n",t);}return 0;
}

一、目标题目： 跳数约束最短路径问题

当信息在计算机网络中传输，通常需要寻找一条有效的最短路径。给定一个无向网络G=(V,A,C)，其中V是节点集合，A是无向边集合，C是边路径长度集合，对于每条边a(i,j)，对应有c(i,j)>=0。当给定两节点（源点和汇点）以及跳数pathLength，求解两点之间的最短距离，要求其跳数满足大于pathLength。

   要求：测试一下结果，看看花费的时间，时间复杂度是多少，结果是否正确

二、时间复杂度：  O（VE）

SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

三、算法思路：

参考spfa算法来做，spfa是bellman-ford算法的队列优化版本，spfa算法是用来求单源最短路径的一种算法——用数组Dp记录每个结点的最短路径估计值，用邻接表来存储图G。采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

四、实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

五、运行案例：

  1.题目数据

 a.7个节点 12条链路 跳数约束为2

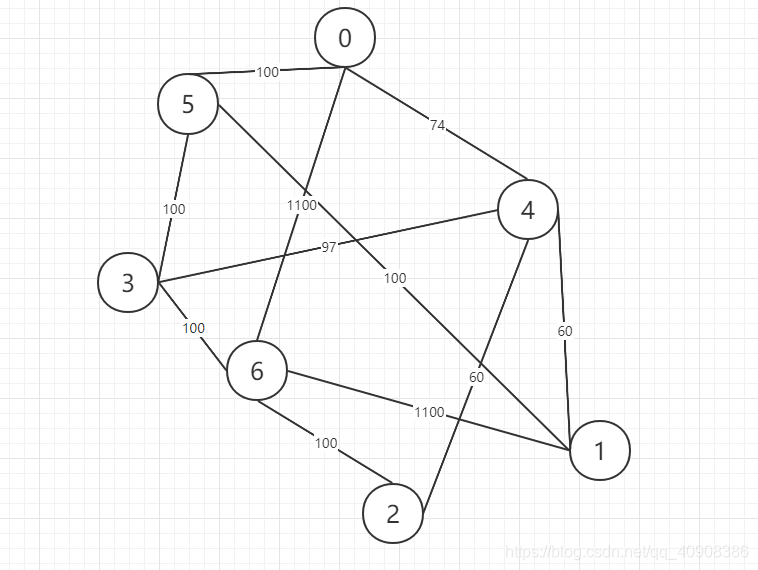
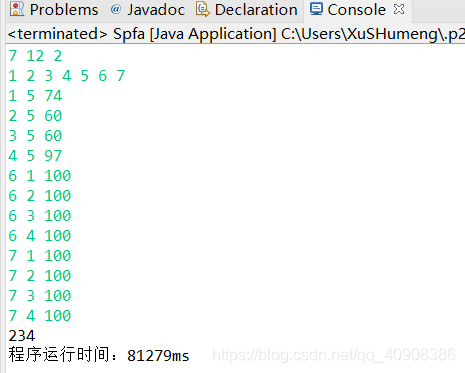
此测试数据经测试与考虑重复经过是结果一样

最终满足跳数限制2的路径数据为1->5->2->7 路径最短为234

b．举出简单案例并进行测试

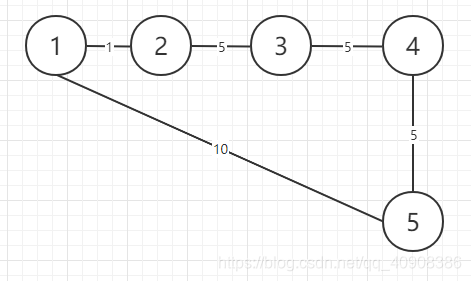
5个节点 5条路径 跳数限制为6

1 2 1

2 3 5

3 4 5

4 5 5

1 5 10

满足跳数约束的最短路径为 1->2->1->2->1->2->1->5 最短路径为16

经测试所编译算法满足要求

c．再次测试一组数据

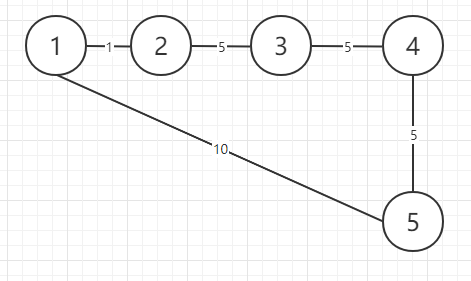
4个节点 4条路径 跳数限制为5

由1到3的最短路径

1 2 1

2 3 2

1 3 100

3 4 1

1 3 5

测试满足跳数约束的最短路径为

1->2->1->2->3->4->3

满足约束条件最短路径长度为6

测试成功

JAVA代码：

  Node.java

public class Node {private int v,len;public Node() {}public  int getV() {return this.v;}public  void setV(int v) {this.v = v;}public  int getLen() {return this.len;}public  void setLen(int len) {this.len = len;}
}

Snode.java

public class Snode {private int to,w,next;public Snode() {}public Snode(int to,int w,int next) {this.to= to;this.w= w;this.next= next;}public  int getTo() {return this.to;}public  void setTo(int to) {this.to = to;}public  int getW() {return this.w;}public  void setW(int w) {this.w = w;}public  int getNext() {return next;}public  void setNext(int next) {this.next = next;}
}

Spfa.java

import java.util.ArrayList;
import java.util.Scanner;public class Spfa {//本题需要在在spfa算法基础上应用dynamic-programming方法，其状态转移方程为：令dp[i,j]为“从源点s到达节点i，且至少经过j条边的最短路径长度，则dp【i,j]=min{dp[k,j-1]+dist[k,i]},其中k表示与节点i相邻的节点号，dist[k,i]表示节点k与i之间的距离static int MAX = 5010;static int Dp[][] = new int[MAX][505];//可以处理规模为跳跃505次以下的问题static int pre[] = new int[MAX];//pre[e]指边e在前向星的边表中e的前继边static int Index;//index用于表示边的索引static int visit[][] = new int[MAX][505];//维护一个visit表，防止节点重复进入spfa的优化队列static int INF = 1061109567;//定义INF为无穷大static Snode[] Edge = new Snode[20000];//初始化前向星中的边表static Node[] listb = new Node[20000];//初始化spfa算法中的优化队列static Node v1;static Node v2;//v1与v2用作临时变量//前向星数据结构的辅助函数，用于将无向边添加到前向星的边表中static void Add_edge(int a, int b, int c) {Edge[Index].setTo(b);//该边的终点为bEdge[Index].setW(c);//该边的权重为cEdge[Index].setNext(pre[a]);//该边的上一条边为pre[a]pre[a] = Index++;//将该边设为“下一条边的上一条边”，即为下一条边更新pre[a]的值}//spfa算法的入口，接受a，b，c三个参数，解决“从a到b至少经过c条边的最短距离”的问题static int SPFA(int a, int b, int c) {int s, e, i, vv, vlen;//s与e，即start与end，分别代表spfa队列的队头与队尾//在spfa算法运行时，会维护一个“当前点”的概念，i用于遍历“当前点”的所有边//vv代表“当前点”经过边i所到达的点//vlen代表到达vv时所经过的边的数量//初始化visit表，当且仅当visit[i,j]的值为假时，状态dp[i,j]不在spfa的优化队列中             for (int j = 0; j < visit.length; j++) {for (int j2 = 0; j2 < 505; j2++) {visit[j][j2] = 0;}}//初始化spfa的优化队列s = 0;e = 0;Dp[a][0] = 0;//为dynamic-programming方法设置初始状态，该状态的含义是显然的：从a点到a点，至少经历0条边的最短距离为0    从源点s到达节点i，且至少经过j条边的最短路径长度//用源点a来初始化状态v1，该状态的节点号为a，经过的路径长为0v1 = new Node();v1.setV(a);v1.setLen(0);//将v1入队listb[s++] = v1;while (s != e) {//与基础spfa算法一致，当优化队列不再有状态时，表示所有点到源点的最短路径已经确定，算法结束//将队头的状态出队，存入v1，此时v1即为前文所提到的“当前点”，并将其对应的visit表的值设为假v1 = listb[e++];visit[v1.getV()][v1.getLen()] = 0;for (i = pre[v1.getV()]; i != -1; i = Edge[i].getNext()) {//遍历与“当前点”相连的所有边vlen = v1.getLen() + 1;//通过与“当前点”所连点边到达的前，其经历的边数为“当前点”经历的边数加一//该操作为一个剪枝操作，其原理是将已经经历超过c条边的状态，都合并到正好经历c条边的状态上，以此来减少dp方法的状态数，但不影响结果if (vlen >= c) {vlen = c;      }//vv代表“当前点”经过边i所到达的点vv = Edge[i].getTo();//此处为执行状态转移方程的核心代码，其语义为：dp【i,j]=min{dp[k,j-1]+dist[k,i]},其中k表示与节点i相邻的节点号，dist[k,i]表示节点k与i之间的距离if (Dp[vv][vlen] > Dp[v1.getV()][v1.getLen()] + Edge[i].getW()) {Dp[vv][vlen] = Dp[v1.getV()][v1.getLen()] + Edge[i].getW();// 将被更新的状态加入spfa优化队列，同时防止将重复状态入队if (visit[vv][vlen] == 0) {v2 = new Node();v2.setV(vv);v2.setLen(vlen);//状态入队后将其对应的visit表的值设为真visit[vv][vlen] = 1;listb[s++] = v2;}}}}return Dp[b][c];}public static void main(String[] args) {long start = System.currentTimeMillis();int i, j, n, m, a, b, c, t;Scanner inputScanner = new Scanner(System.in);//初始化 边对象 数组for (i = 0; i < 20000; i++) {Edge[i] = new Snode();}//初始化 节点对象 数组for (i = 0; i < 20000; i++) {listb[i] = new Node();}Index = 0;for (int k = 0; k < pre.length; k++) {pre[k] = -1;}for (int k = 0; k < Dp.length; k++) {for (int k2 = 0; k2 < 505; k2++) {Dp[k][k2] = INF;}}//		n 顶点数
//		m边数
//		require 条数n = inputScanner.nextInt();m = inputScanner.nextInt();int require = inputScanner.nextInt();int vertex[] = new int[n];
//		录入顶点数for (int k = 0; k < n; k++) {vertex[k] = inputScanner.nextInt();}
//		录入边 权for (i = 1; i <= m; i++) {a = inputScanner.nextInt();b = inputScanner.nextInt();c = inputScanner.nextInt();Add_edge(a, b, c);Add_edge(b, a, c);}t = SPFA(vertex[0], vertex[n - 1], require);if (t == INF) {System.out.println("-1");} else {System.out.println(t);}long end = System.currentTimeMillis();System.out.println("程序运行时间："+(end-start)+"ms");}}