本文主要是介绍算法:贪心算法的原理和基本思路,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 写在前面
- 贪心算法
- 初步认知
- 找零问题
- 最短路径问题
- 典型例题
- 柠檬水找零
- 将数组减半的最少操作次数
- 最大数
- 摆动序列
写在前面
本篇开始总结贪心算法的原理和思路,本篇主要是对贪心有一个基本的认知和做题的逻辑思路,在理清逻辑的前提下进行解题会轻松许多,后续进行题量的累积以获得更多的算法思路和解题经验
贪心算法
什么是贪心算法?
贪心算法是很重要的一类算法,它解题的核心是找到一种贪心的策略,能够将解决问题的策略从局部最优转换成全局最优
如何解决贪心问题?
- 把解决问题的步骤可以划分为若干步
- 解决每一个步骤的时候,都选择看起来是一个最优的解法
- 希望可以得到全局的最优解
贪心算法的特点?
- 从贪心策略提出的角度来讲:
- 贪心策略的提出是没有固定的标准和模板
- 贪心策略每道题都可能会不一样
- 从贪心策略正确性的角度来讲:
- 贪心策略并不一定是正确的
- 因此正确的贪心策略是需要被证明的
初步认知
下面从几个经典的问题,从贪心的角度来看题
找零问题
这是一类很经典的题目,例如现在去超市买东西,售货员收到了50元的纸币,物品是4元钱,售货员要找出46元,现在她有20,10,5,1元纸币若干张,现在要让找出的纸币数量是最少的,应该如何解决?
对待这个问题,如果直观去想其实是很简单的,只需要2张20,1张5元,1张1元即可凑够46元,但是这是直观去想的,如果转换成代码逻辑?
如果考虑的贪心策略是,将需要的钱数从面额大的情况开始找,每次都在大面额的纸币找不到的前提下再去找次大的纸币,根据这样的贪心策略的确可以找到一个方案,但是这个方案的正确性却有待考证,放在这个题当然正确,但如果是下面的题型:
给定某国家纸币面额有20元,18元,10元,5元,1元,现在要找够36元,如果再使用刚才的思路,那么就应该要找1张20元,1张10元,1张5元,1张1元,但是实际上,只需要2张18元的纸币就足够了,这说明上面的算法策略是有问题的,不可以使用这样的算法策略
最短路径问题
现在给定一个3x3的表格,其中每个格子的数据代表距离,现在要求从格子的左上角走到右下角最少需要走多少距离?
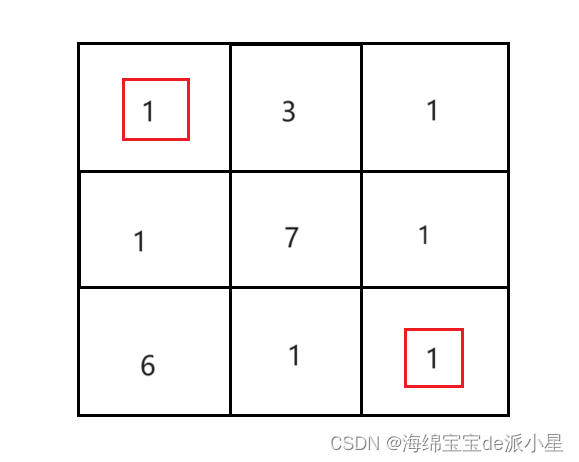
现在想一种贪心策略,每次比较格子四周的数值,选择最小的那个数值去寻路,那么对于上图来说可以寻路出这样的路
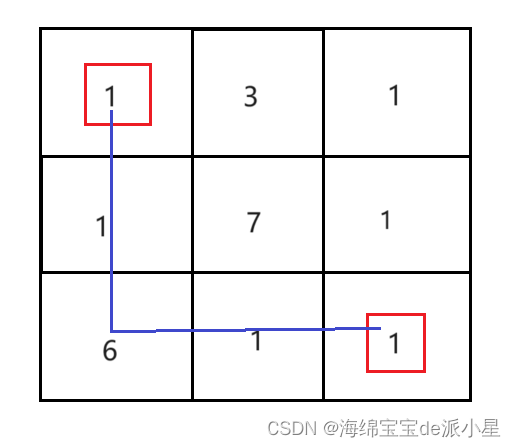
但是这样的路很明显不如走另外一个直角路,这说明贪心策略也是有问题的,这也进一步的说明了现在寻找出的贪心策略并不一定是正确的,还需要进行后续的步骤才能说明这个贪心策略是正确的
下面使用几个例题来解决上面的问题:
典型例题
柠檬水找零

贪心策略
对于这个题来说,贪心策略就是给五元就收下,给十元就找五元,给二十元就找十元和五元,这是正确的贪心策略,如果给二十元找三张五元这就是一个错误的贪心策略
代码解析
class Solution
{
public:bool lemonadeChange(vector<int>& bills) {int five=0,ten=0;for(auto x : bills){if(x==5){five++;}else if(x==10){if(five==0){return false;}else{five--;ten++;}}else{if(ten && five){ten--;five--;}else if(five>=3){five-=3;}else{return false;}}}return true;}
};
将数组减半的最少操作次数

本题的贪心策略也比较简单,直接找最大的数减半
唯一要注意的是,这里可以采用一个大根堆的数据结构来解决,代码实现也很容易
class Solution
{
public:int halveArray(vector<int>& nums) {priority_queue<double> heap;double sum=0.0;for(auto x : nums){heap.push(x);sum+=x;}sum /= 2;int count=0;while(sum>0){double t=heap.top()/2;heap.pop();sum-=t;count++;heap.push(t);}return count;}
};
最大数

此题的贪心策略是,使用一个比较函数进行比较,根据字符串中的先后大小顺序选出可以组成的最大的数,贪心的比较策略就是让字符串两两相加,谁大选谁即可
class Solution
{
public:string largestNumber(vector<int>& nums){vector<string> v;for (auto x : nums){v.push_back(to_string(x));}sort(v.begin(), v.end(), [](const string& s1, const string& s2){return (s1 + s2) > (s2 + s1);});string res;for (auto x : v){res += x;}if (res[0] == '0'){return "0";}return res;}
};
摆动序列

本题的贪心策略是找拐点,对于这个题来说,如果把数组中的元素放到一个折线图中,那么贪心策略就是找到每一次的拐点即可,那么根据这个原理只需要统计出每一次的拐点就可以
对于统计拐点的思路来说,定义一个left和right状态值,表示的是现在这个情况下下一个目标值的状态和现在是否一样,如果一样则说明不是拐点,如果不一样就说明状态由递增转换为递减或者是由递减转换为递增,基于这个原理就可以进行代码的编写解决问题了
class Solution
{
public:int wiggleMaxLength(vector<int>& nums) {int left=0,right=0,count=0;if(nums.size()<2){return nums.size();}for(int i=0;i<nums.size()-1;i++){right=nums[i+1]-nums[i];if(right==0){continue;}if(left*right<=0){count++;}left=right;}return count+1;}
};
这篇关于算法:贪心算法的原理和基本思路的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






