智能优化算法改进-K-means聚类种群初始化附Matlab代码

目录

0引言

一、K-means聚类原理

二、K-Means聚类算法步骤

三、K-Means聚类原理图​编辑

四、K-means聚类改进智能优化算法种群初始化效果图

4.1  初始种群数据图

​4.2  K-means聚类结果图

4.2.1  根据K-means聚类原理聚类

 4.2.2  根据MATLAB自带kmeans函数聚类

 五、K-means聚类改进智能优化算法种群初始化Matlab部分代码

0引言

       智能优化算法种群初始化的改进是改进中常用策略，比如说混沌种群初始化、佳点集、精英反向学习策略等等，根据阅读文献，K-means聚类可以改进智能优化算法种群初始化，如SASSA，它的策略为K-means聚类种群+正余弦算法改进加入者策略+自适应策略扰动。

一、K-means聚类原理

        K-Means算法是一种典型的基于划分的聚类算法，也是一种无监督学习算法。K-Means算法的思想很简单，对给定的样本集，用欧氏距离作为衡量数据对象间相似度的指标，相似度与数据对象间的距离成反比，相似度越大，距离越小。预先指定初始聚类数以及个初始聚类中心，按照样本之间的距离大小，把样本集划分为个簇根据数据对象与聚类中心之间的相似度，不断更新聚类中心的位置，不断降低类簇的误差平方和（Sum of Squared Error，SSE），当SSE不再变化或目标函数收敛时，聚类结束，得到最终结果。K-Means算法的核心思想：首先从数据集中随机选取k个初始聚类中心，计算其余数据对象与与聚类中心的欧氏距离，找出离目标数据对象最近的聚类中心，并将数据对象分配到聚类中心所对应的簇中。然后计算每个簇中数据对象的平均值作为新的聚类中心，进行下一次迭代，直到聚类中心不再变化或达到最大的迭代次数时停止。空间中数据对象与聚类中心间的欧氏距离计算公式为：

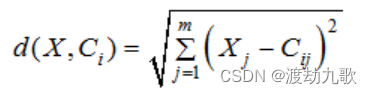
其中，为数据对象；为第i个聚类中心；为数据对象的维度；，为和的第个属性值。

二、K-Means聚类算法步骤

       K-means算法是典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

K-mean算法步骤如下：

1）随机选取K个样本为中心

2）分别计算所有样本到随机选取的K个中⼼的距离

3）样本离哪个中⼼近就被分到哪个中⼼

4）计算各个中⼼样本的均值（最简单的⽅法就是求样本每个维度的平均值）作为新的中心

5）重复（2）（3）（4）直到新的中⼼和原来的中⼼基本不变化的时候，算法结束

三、K-Means聚类原理图

四、K-means聚类改进智能优化算法种群初始化效果图

4.1  初始种群数据图

clc;
clear;
close all;
dim=2;%问题维度
pop=200;%种群数量
x_lower = 20e-9;            % 搜索变量x范围下限
y_lower = 0.55;             % 搜索变量y范围下限
x_upper = 500e-9;           % 搜索变量x范围上限
y_upper = 1;                % 搜索变量y范围上限
for i = 1:popdata(i, 1) = x_lower + (x_upper - x_lower) * rand;data(i, 2) = y_lower + (y_upper - y_lower) * rand;  %初始化种群
end

4.2  K-means聚类结果图

4.2.1  根据K-means聚类原理聚类

聚类数为4时聚类结果：

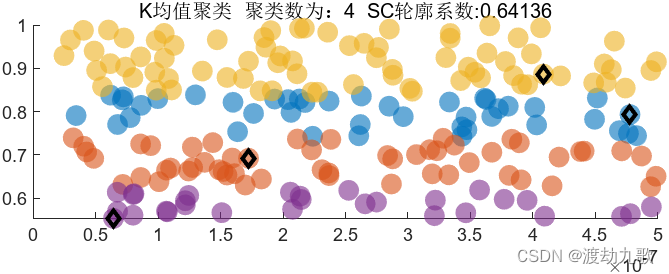
 聚类数为5时聚类结果：

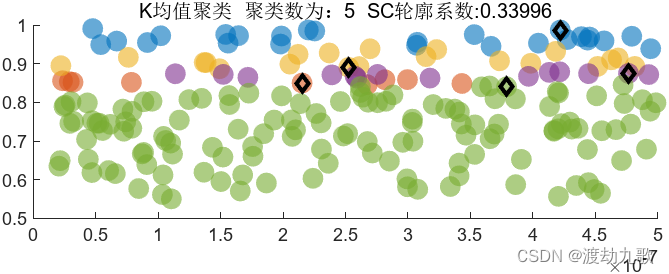
 聚类数为6时聚类结果：

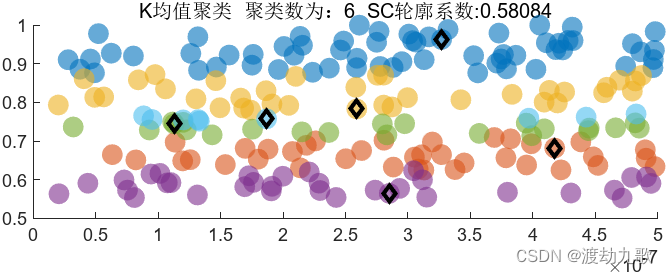
 4.2.2  根据MATLAB自带kmeans函数聚类

 聚类数为4时聚类结果：

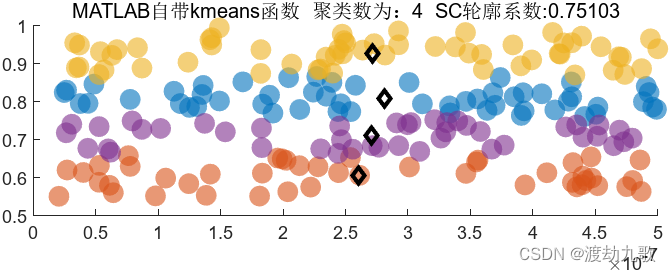
 聚类数为5时聚类结果：

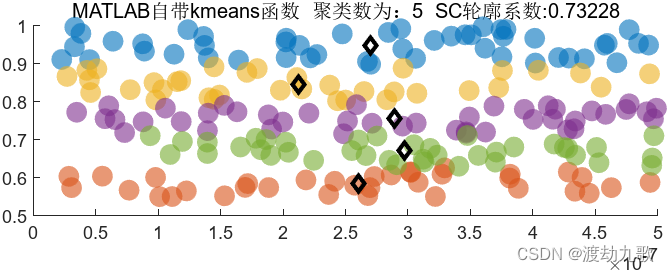  聚类数为6时聚类结果：

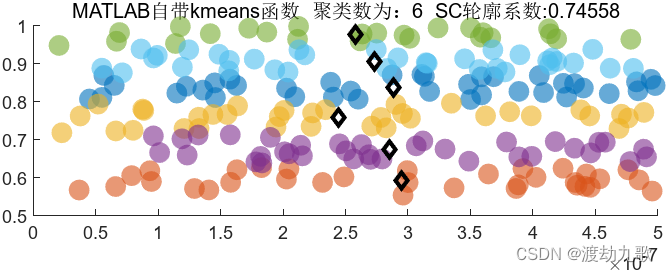
 五、K-means聚类改进智能优化算法种群初始化Matlab部分代码

clc;
clear;
close all;
dim=2;%问题维度
pop=200;%种群数量
x_lower = 20e-9;            % 搜索变量x范围下限
y_lower = 0.55;             % 搜索变量y范围下限
x_upper = 500e-9;           % 搜索变量x范围上限
y_upper = 1;                % 搜索变量y范围上限
for i = 1:popdata(i, 1) = x_lower + (x_upper - x_lower) * rand;data(i, 2) = y_lower + (y_upper - y_lower) * rand;  %初始化种群
end
%% 原理推导K均值
[m,n]=size(data);
cluster_num=6;
cluster=data(randperm(m,cluster_num),:);......%% 画出聚类效果
figure(2)
subplot(2,1,1)
a=unique(index_cluster); %找出分类出的个数
C=cell(1,length(a));
for i=1:length(a)C(1,i)={find(index_cluster==a(i))};
end
for j=1:cluster_numdata_get=data(C{1,j},:);scatter(data_get(:,1),data_get(:,2),100,'filled','MarkerFaceAlpha',.6,'MarkerEdgeAlpha',.9);hold on
end
sc_t=mean(silhouette(data,index_cluster'));
title_str=['K均值聚类','  聚类数为：',num2str(cluster_num),'  SC轮廓系数:',num2str(sc_t)];