java调用cplex实现拉格朗日松弛算法求解整数规划问题

2023-10-12 22:20
文章标签 java 算法 规划 实现 问题 调用 整数 拉格朗 求解 松弛 cplex

本文主要是介绍java调用cplex实现拉格朗日松弛算法求解整数规划问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

拉格朗日松弛算法

在难以求解的模型当中，可以使用分支定界算法，割平面算法等算法进行精确求解，以便于获得问题的精确解。若在求解过程中，这些难以求解的模型不需要获得他的精确解，而是只需要给出一个次优解或者解的上下界。在这种情况下可以考虑采用松弛模型的方法。当然，智能算法也是一种解决途径。

对于一个整数规划问题，与0-1整数规划问题中将离散变量的取值范围松弛为[0,1]之间的连续变量不同，拉格朗日松弛算法是将模型中的部分约束进行松弛，并且这些被松弛的约束并不是被完全去掉，而是利用拉格朗日乘子在目标函数上增加相应的惩罚项，对不满足这些约束条件的解进行惩罚。

算法基础

目前，拉格朗日松弛算法已经被应用于定价问题，选址问题，分配问题以及路径优化问题等诸多组合优化问题且效果较好。
考虑以下包含等式约束和不等式约束的整数规划模型（P），A和b是等式约束的系数集合和右端项；D和e是不等式约束的系数集合和右端项，c是目标函数系数集合，x是模型的决策变量。
在这里插入图片描述
在模型当中，等式约束显然比不等式约束的约束力要强，或者说成立条件更为严格，这样的约束被称为难约束，相对应的是简单约束。因而在使用松弛算法的过程中，一般将难约束进行松弛处理。在一些特殊问题中具备如式子Ax+By=f的变量x和y耦合的约束，一般将其进行松弛处理以便于形成多个变量独立的子问题。因而，在处理松弛约束时，存在以下两种方式：
（1）直接将难约束进行松弛处理，并将其作为目标函数的惩罚项，得到一个子问题，作为主问题的下界或者上界，这被称为约束松弛；
（2）将耦合约束进行松弛处理，并将其在目标函数进行整合，分离出多个子问题，而子问题的目标函数加权为主问题的下界或者上界，这被称为问题分解；

通过（1）方式将Ax=b添加到目标函数，得到拉格朗日松弛问题（LR），其中mu表示拉格朗日乘子。
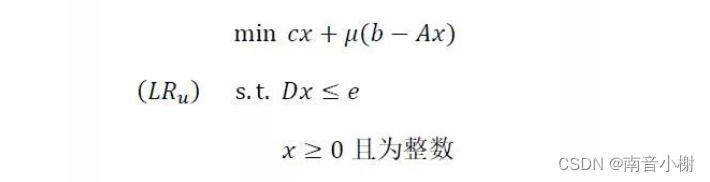
在这里插入图片描述
通过松弛问题，选择合适的拉格朗日乘子即可实现原问题的解且约束式更少，求解更为简单。因而，拉格朗日乘子mu关系到原问题解的效果优劣。那么如何选择合适的乘子呢？固定变量x并对mu进行求解是可行的方法，也就是采用松弛问题的对偶问题进行求解（对偶问题一定是凸问题，但相关证明不太清楚）。松弛问题（LR）的对偶问题（D）表示为：
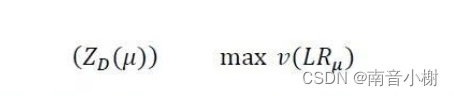
在这里插入图片描述
对于最小化问题，对偶问题的解小于等于原问题的解，相关证明参考【拉格朗日松弛算法】以及【拉格朗日松弛介绍】。
在这里插入图片描述

次梯度方法

拉格朗日松弛算法主要有两种方法，一种是次梯度算法，另一种是拉格朗日启发算法。次梯度算法是经典的求解方式，其思路是通过循环迭代确定合适的拉格朗日乘子，并求出对应的最优解且对解进行可行化处理，主要分为乘子更新，步长更新和迭代终止三大部分。
（1）乘子更新
拉格朗日乘子更新规则如下：
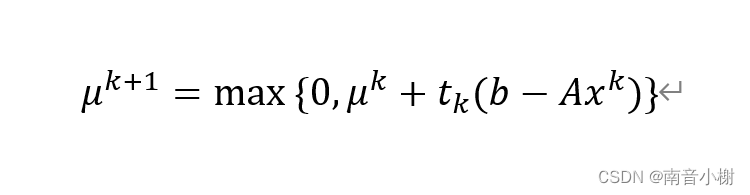
在这里插入图片描述
其中，k表示迭代次数，t_k表示第k次迭代的步长，x_k表示第k次迭代的松弛问题的解。
通过迭代规则，是的乘子始终大于等于0且根据松弛约束进行改善以便于生成合适的乘子。
（2）步长更新
乘子更新时需要借助迭代步长，而步长计算方式来源于以下公式：
在这里插入图片描述
（3）终止条件
在这里插入图片描述

算法流程

（1）初始化参数，包括上界，下界，迭代步长以及拉格朗日乘子；
（2）求解拉格朗日松弛问题，得到解方案；
（3）计算当前迭代下的上界；
（4）若当前上界小于最好上界，则更新上界；
（5）判断解方案是否可行；若可行，则更新下界；
（6）更新迭代步长；
（7）若连续一定次数未更新，则lambda减半；
（8）更新拉格朗日乘子；
（9）判断是否满足终止条件。

求解示例

在这里插入图片描述
将约束1进行松弛，得到拉格朗日松弛问题：
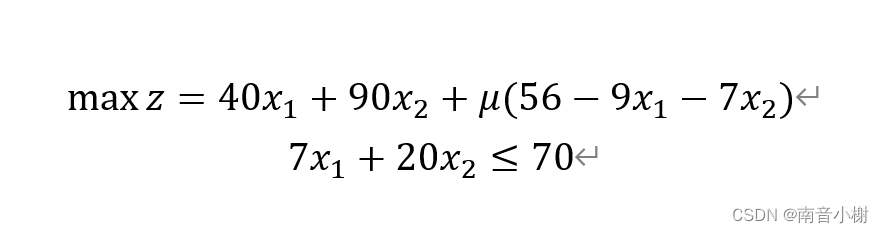
在这里插入图片描述
第一次迭代过程如下：
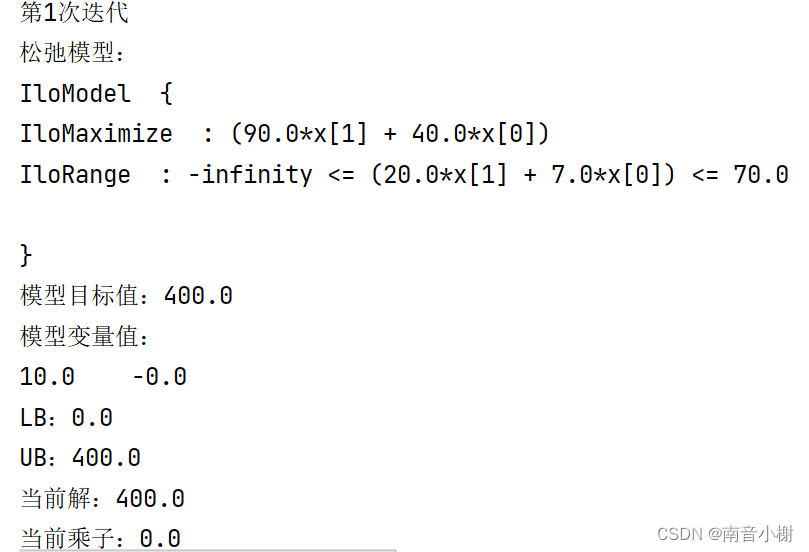
在这里插入图片描述
第二次迭代过程如下：
在这里插入图片描述
最终迭代结果如下：
在这里插入图片描述

算法代码

import ilog.concert.IloException;
import ilog.concert.IloNumExpr;
import ilog.concert.IloNumVar;
import ilog.concert.IloNumVarType;
import ilog.cplex.IloCplex;//调用cplex实现拉格朗日松弛算法求解整数规划
//整数规划示例：
//max z=40x_1+90x_2
//9x_1+7x_2<=56
//7x_1+20x_2<=70
//x_1,x_2>=0且为整数
//最优值：x_1=4,x_2=2,z=340//数据参数定义
class ModelData2{//目标系数double[] objectiveCoefficient={40,90};//约束系数double[][] constraintCoefficient={{9,7}, {7,20}};//约束值double[] constraintValue={56,70};//变量数量int variableNumber=2;//约束数量int constrainNumber=2;//模型下界double lowBound=Double.MIN_VALUE;
}//使用cplex-拉格朗日松弛算法求解整数规划
public class LagrangianRelaxationDemo {//定义数据ModelData2 data;//定义上界double UB;//定义下界double LB;//定义乘子double mu;double bestMu;//定义迭代步长double stepSize;double minStepSize;//定义迭代次数int iter;//模型对象IloCplex model;//模型变量IloNumVar[] x;//变量对应的取值double[] varsValue;double[] bestValue;//模型目标值double modelObj;//构造函数public LagrangianRelaxationDemo(ModelData2 data){this.data=data;LB=0;UB=Double.MAX_VALUE;stepSize=1;minStepSize=0.001;iter=50;mu=0;varsValue=new double[data.variableNumber];bestValue=new double[data.variableNumber];}//松弛模型建立-将约束1进行松弛private void buildModel() throws IloException {model=new IloCplex();model.setOut(null);x=new IloNumVar[data.variableNumber];for(int i=0;i<data.variableNumber;i++){x[i]=model.numVar(0,1e15, IloNumVarType.Int,"x["+i+"]");}//设置目标函数IloNumExpr obj = model.numExpr();for(int i=0;i<data.variableNumber;i++){obj=model.sum(obj,model.prod(data.objectiveCoefficient[i],x[i]));}//添加松弛约束obj=model.sum(obj,56*mu);obj=model.sum(obj,model.prod(-9*mu,x[0]));obj=model.sum(obj,model.prod(-7*mu,x[1]));
//        System.out.println(obj);model.addMaximize(obj);//添加约束for(int k=1;k<data.constrainNumber;k++){IloNumExpr expr = model.numExpr();for(int i=0;i<data.variableNumber;i++){expr=model.sum(expr,model.prod(data.constraintCoefficient[k][i],x[i]));}model.addLe(expr,data.constraintValue[k]);}}//更新模型目标中的乘子-更新模型private void updateModelObj(double mu) throws IloException {//设置目标函数IloNumExpr objTem = model.numExpr();for(int i=0;i<data.variableNumber;i++){objTem=model.sum(objTem,model.prod(data.objectiveCoefficient[i],x[i]));}//添加松弛约束objTem=model.sum(objTem,56*mu);objTem=model.sum(objTem,model.prod(-9*mu,x[0]));objTem=model.sum(objTem,model.prod(-7*mu,x[1]));//清除模型目标函数model.getObjective().clearExpr();model.getObjective().setExpr(objTem);}//模型求解private void solveModel() throws IloException {if (model.solve()){modelObj=model.getObjValue();System.out.println("模型目标值："+model.getObjValue());System.out.println("模型变量值：");for(int i=0;i< data.variableNumber;i++){varsValue[i]=model.getValue(x[i]);System.out.print(model.getValue(x[i])+"\t");}System.out.println();}else{modelObj=Double.MAX_VALUE;System.out.println("模型目标值："+model.getObjValue());System.out.println("模型变量值：");for(int i=0;i< data.variableNumber;i++){varsValue[i]=-1;System.out.print(varsValue[i]+"\t");}System.out.println("模型不可解");}}//次梯度迭代算法更新mu过程private void updateMu() throws IloException {//建立松弛模型buildModel();System.out.println(model);System.out.println();//次梯度方法的标量【0,2】double lambda = 2;//是否有效更新int isImprove = 0;int maxImprove = 3;int count=0;while(count++<iter){System.out.println("******************************");System.out.println("第" + count +"次迭代");//根据当前mu值调整模型目标函数updateModelObj(mu);System.out.println("松弛模型：");System.out.println(model);//模型求解solveModel();//更新上界if(modelObj<UB){UB=modelObj;isImprove=0;bestMu=mu;for(int i = 0; i < bestValue.length; i++) {bestValue[i] = varsValue[i];}}else{//记录未更新的次数isImprove++;}System.out.println("LB：" + LB);System.out.println("UB：" + UB);System.out.println("当前解：" + modelObj);System.out.println("当前乘子：" + mu);//更新mudouble subgradient=-1*data.constraintValue[0];for(int i=0;i< data.variableNumber;i++){subgradient+=data.constraintCoefficient[0][i]*varsValue[i];}mu=Math.max(0, mu + stepSize * subgradient);//判断可行解是否满足原问题(约束1)，并将其作为下界if(subgradient<=0){double curLB=0;for(int i=0;i< data.variableNumber;i++){curLB+=data.objectiveCoefficient[i]*varsValue[i];}if(curLB>LB)LB=curLB;}//未更新达到次数，对次梯度算法的标量进行减半处理if(isImprove>=maxImprove){lambda /=2;isImprove=0;}//迭代终止条件//若上下界差趋近于0，则接近最优解if(LB>=UB-1e-5)break;//若松弛约束趋近于0，则接近最优解double consDist=Math.pow(subgradient,2);if(consDist<=1e-5)break;//若迭代小于规定的步长，则停止stepSize=lambda*(modelObj-LB)/(consDist+1e-5);if(stepSize<minStepSize)break;}System.out.println("========================");System.out.println("mu："+bestMu);System.out.println("LB：" + LB);System.out.println("UB:：" + UB);double gap = Math.round((UB - LB) *  10000 / UB) / 100;System.out.println("gap: " + gap + "%");System.out.println("模型变量值：");for(int i = 0; i < bestValue.length; i++)System.out.print(bestValue[i]+"\t");}public static void main(String[] args)throws IloException{ModelData2 data =new ModelData2();LagrangianRelaxationDemo lp=new LagrangianRelaxationDemo(data);lp.updateMu();}
}

========================================
今天到此为止，后续记录其他cplex技术的学习过程。
以上学习笔记，如有侵犯，请立即联系并删除！

这篇关于java调用cplex实现拉格朗日松弛算法求解整数规划问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/198824。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
Spring Security 基于表达式的权限控制

Spring Security 基于表达式的权限控制

前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
阅读更多...
浅析Spring Security认证过程

浅析Spring Security认证过程

类图 为了方便理解Spring Security认证流程，特意画了如下的类图，包含相关的核心认证类 概述 核心验证器 AuthenticationManager 该对象提供了认证方法的入口，接收一个Authentiaton对象作为参数; public interface AuthenticationManager {Authentication authenticate(Authenti
阅读更多...
Spring Security--Architecture Overview

Spring Security--Architecture Overview

1 核心组件 这一节主要介绍一些在Spring Security中常见且核心的Java类，它们之间的依赖，构建起了整个框架。想要理解整个架构，最起码得对这些类眼熟。 1.1 SecurityContextHolder SecurityContextHolder用于存储安全上下文（security context）的信息。当前操作的用户是谁，该用户是否已经被认证，他拥有哪些角色权限…这些都被保
阅读更多...
Spring Security基于数据库验证流程详解

Spring Security基于数据库验证流程详解

Spring Security 校验流程图 相关解释说明（认真看哦） AbstractAuthenticationProcessingFilter 抽象类 /*** 调用 #requiresAuthentication(HttpServletRequest, HttpServletResponse) 决定是否需要进行验证操作。* 如果需要验证，则会调用 #attemptAuthentica
阅读更多...
Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
Java架构师知识体认识

Java架构师知识体认识

源码分析 常用设计模式 Proxy代理模式Factory工厂模式Singleton单例模式Delegate委派模式Strategy策略模式Prototype原型模式Template模板模式 Spring5 beans 接口实例化代理Bean操作 Context Ioc容器设计原理及高级特性Aop设计原理Factorybean与Beanfactory Transaction 声明式事物
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
Java进阶13讲__第12讲_1/2

Java进阶13讲__第12讲_1/2

多线程、线程池 1.  线程概念 1.1  什么是线程 1.2  线程的好处 2.   创建线程的三种方式 注意事项 2.1  继承Thread类 2.1.1 认识  2.1.2  编码实现  package cn.hdc.oop10.Thread;import org.slf4j.Logger;import org.slf4j.LoggerFactory
阅读更多...
好题——hdu2522（小数问题：求1/n的第一个循环节）

好题——hdu2522（小数问题：求1/n的第一个循环节）

好喜欢这题，第一次做小数问题，一开始真心没思路，然后参考了网上的一些资料。 知识点***********************************无限不循环小数即无理数，不能写作两整数之比*****************************（一开始没想到，小学没学好） 此题1/n肯定是一个有限循环小数，了解这些后就能做此题了。 按照除法的机制，用一个函数表示出来就可以了，代码如下
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2