LeetCode20天刷题计划之Day8-深度优先搜索二叉树

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

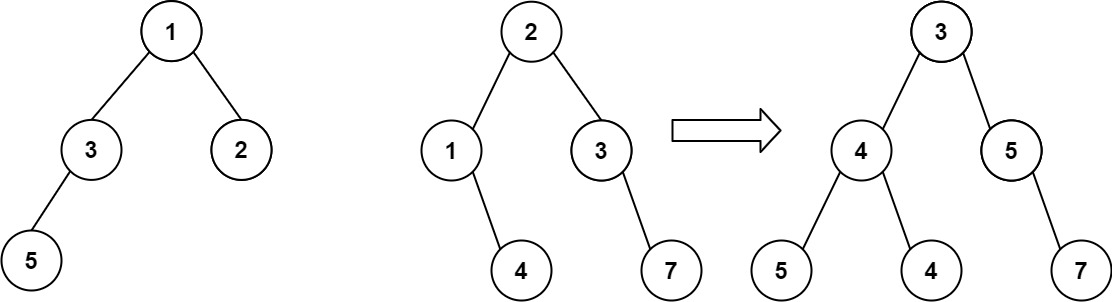
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• -104 <= Node.val <= 104

 注：本题相当于是个二叉树遍历，方式是前序遍历(跟->左->右),一个很好的解决方式就是以第一棵树作为基础，然后判断第二棵树的节点是否需要更新并在第一棵树上更新。相同的节点有值就进行合并，同一个节点只有一个值就采用这个值，同一个节点都为null就停止。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 == nullptr) {return root2;}if (root2 == nullptr) {return root1;}//以左边二叉树为基础，将右边二叉树的值进行合并root1->val = root1->val + root2->val;root1->left = mergeTrees(root1->left, root2->left);root1->right = mergeTrees(root1->right, root2->right);return root1;}
};

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {int val;Node *left;Node *right;Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

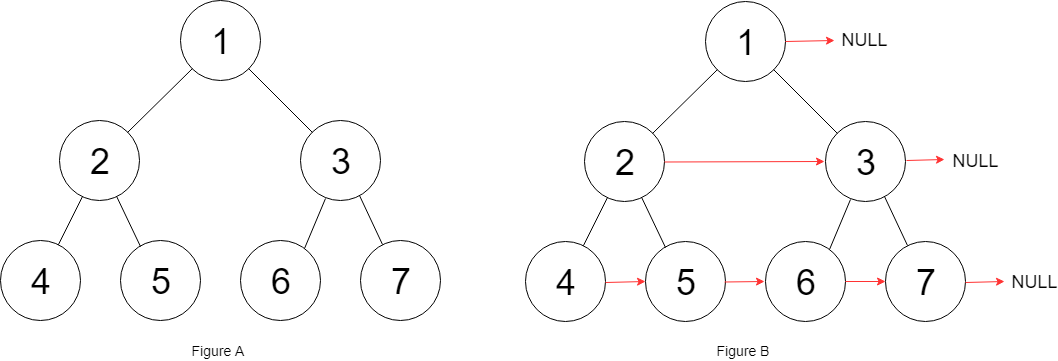
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

提示：

• 树中节点的数量在 [0, 212 - 1] 范围内
• -1000 <= node.val <= 1000

注： 本题可以理解为将二叉树的每一层连接成一个链表，可以用二叉树的层序遍历来进行操作。将每一层的节点拿出来遍历并进行连接。在遍历的过程中同时修改每个节点的next指针。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:Node* connect(Node* root) {if(root == nullptr){return root;}//初始化队列同时将第一层的跟节点加入队列queue<Node*> Q;Q.push(root);while(!Q.empty()){int size = Q.size();//记录队列大小//遍历所有节点for(int i = 0; i < size; i++){Node* node = Q.front();//从队首取出元素Q.pop();//连接每一层的节点if(i < size - 1) node->next = Q.front();                if(node->left != nullptr) Q.push(node->left);if(node->right != nullptr) Q.push(node->right);}}return root;}
};

以下整理以下二叉树层序遍历模板！ 

//二叉树层序遍历模板
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;// 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;}
};