本文主要是介绍矩陣分析-線性系統-2 高斯消元法、高斯－若爾當消元法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
http://www.cnblogs.com/1. 高斯消元法
高斯消元法（Gaussian elimination）是求解線性方陣組的一種算法，
以下面方程組為例，它的執行步驟為
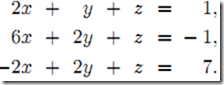
1）構造增廣矩陣，即系數矩陣A增加上常數向量b（A|b）
2）通過以交換行、
某行乘以非負常數和兩行相加這三種初等變化將原系統轉化為更簡單 的三角形式（triangular form） 注：這裡的初等變化可以通過系數矩陣A乘上初等矩陣E來實現
3）從而得到簡化的三角方陣組，注意它更容易解
4）這時可以使用向後替換算法（Algorithm for Back Substitution）求解得
z=-4/-4=1, y=4-2z=4-2=2, x= (1-y-z)/2=(1-2-1)/2=-1
總結上面過程，高斯消元法其實就是下面非常簡單的過程
原線性方程組 ——> 高斯消元法 ——> 下三角或上三角形式的線性方程組 ——> 前向替換算法求解（對於上三角形式，采用後向替換算法）
2.高斯－若爾當消元法（Gauss-Jordan Elimination）
相對於高斯消元法，高斯－
例子如下：
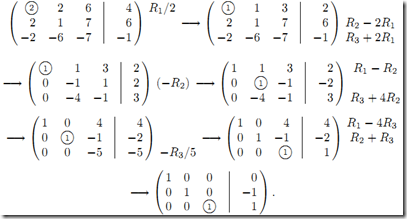解為
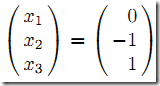
3.實際應用中的高斯消元法
前面介紹了最基本的高斯消元法，
3.1 誤差
因為實際應用中，我們總是利用計算機來分析線性系統，
一個t位（即精度為t）以
為基的浮點數的表達形式為：
，
。
為最接近x的浮點數，
。
例1：對2位以10為基的浮點算法，
。
例2：同樣考慮
，
。
以下面系統為例，看看在高斯消元中采用浮點算法會產生什麼效果。
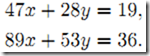
當以精確解法時，通過將第一行乘以m=89/47，
，進而利用後向替換算法得x=1，y=-
當以3位以10為基的浮點算法時，乘子變為
，因為
，
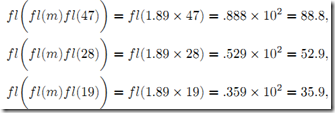。此時，因為不能將第2行第1列位置變為0，
，
。
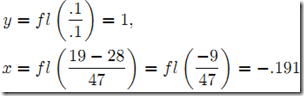3.2 部分主元消元（Partial Pivoting）
盡管無法消除近似誤差的影響，
3.
这篇关于矩陣分析-線性系統-2 高斯消元法、高斯－若爾當消元法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
