本文主要是介绍矩陣算法原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://blog.csdn.net/as3_flash/article/details/2378598
Matrix類的變形方法,最終都是根據用戶給出的參數修改內部矩陣。這些方法的不同之處,在於修改值的算法,以及修改結果在矩陣中的位置。
當用戶在代碼中調用translate(5,13)時,AS3修改矩陣類的內建矩陣,將其中的(tx,ty)T與(5,13)T相加,由於在矩陣創建時(tx,ty)被初始化為(0,0),所以這個結果就是向量(tx,ty)與(5,13)的和。
這個過程如圖所示:
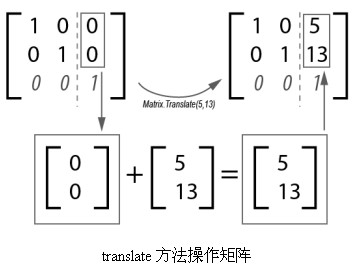
當使用非位移的變換時,這個過程有所改變。根據公式f(x)=Ax+b可知,位移變換是矩陣相加運算,而非位移的變換是矩陣相乘運算。這個過程用代碼可以很清晰地展現,新建項目並在代碼編輯器中寫入以下代碼:
var myMatrix:Matrix=new Matrix;
trace(myMatrix.toString());
myMatrix.scale(4,6);
trace(myMatrix.toString());
myMatrix.scale(2,1);
trace(myMatrix.toString());
本例的操作過程如圖:
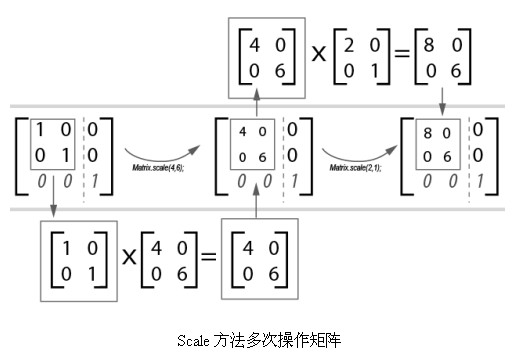
運行,可以觀察到輸出的結果是:
(a=1, b=0, c=0, d=1, tx=0, ty=0)
(a=4, b=0, c=0, d=6, tx=0, ty=0)
(a=8, b=0, c=0, d=6, tx=0, ty=0)
用這種方法,用戶可以研究矩陣類所有方法的內部邏輯。
其實,矩陣類其他內建變形方法的矩陣操作及其圖形學算法都大同小異,其通用模式是:
(1)根據方法的類型,對參數進行數學運算
(2)將運算得出的值,賦予變換矩陣中的相應元素
不同的變換有不同的算法和相關矩陣元素,詳情可以參考表:
表內建方法的矩陣操作和算法
| 名稱 | 詳情 |
| translate(tx, ty) | |
| scale(sx, sy) | |
| rotate(q) |
由此可知,Matrix類的所有內建變形方法都不神秘。它們僅僅是簡化了操作,避免了繁瑣的操作步驟。例如rotate(q)方法,如果使用此方法,用戶只需要一個語句就能完成操作:
DisplayObjectMatrix.rotate(Math.PI/4);
如果不使用這個方法,直接根據其內部機制,操作Matrix類的內部屬性,也能達到相同的結果,但步驟顯然要繁瑣一些:
DisplayObjectMatrix.a=Math.cos(Math.PI/4);
DisplayObjectMatrix.b = Math.sin(Math.PI/4);
DisplayObjectMatrix.c = Math.-sin(Math.PI/4);
DisplayObjectMatrix.d = Math.cos(Math.PI/4);
在動畫中經常會要求創建一些複雜的動畫變形,但使用Matrix類的內建方法的默認行為,在有些場合併不合適。對於初級用戶,因為不具備矩陣知識,面對這種需求只能束手無策。通過前面幾小節的學習,原本看似高深莫測的Matrix類,現在已經一目瞭然不在話下。有了堅實的知識儲備,就能根據Matrix和仿射變換矩陣的原理,手工改變各種內建方法的行為,以及根據所需創建其他變換。下一節,將詳細討論如何利用旋轉變形製作複雜的動畫。
这篇关于矩陣算法原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









