本文主要是介绍Reeds-Shepp和Dubins曲线简介,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
什么是Reeds-Shepp曲线?
想象你下班开车回家,到家后要把车停到车位里。假设你是一个喜欢追求挑战的老司机,想找一条最短的路径把车停进去。那么这样的路径是什么呢?答案就是Reeds-Shepp曲线。Reeds-Shepp曲线由Reeds和Shepp二人在1990年的论文《Optimal paths for a car that goes both forwards and backwards》 [ 1 ] ^{[1]} [1]中提出。
Reeds-Shepp曲线是什么样的曲线?
既然找的是最短路径,我们首先想到的就是直线段,那么它是直线吗?嗯…,在某些特殊情况下,它确实是直线。比如下图左所示的情况,汽车车头或者车尾刚好对准了停车位(绿色表示停车位,红色表示汽车的起始状态,灰色表示汽车)。可是实际显然不会这么简单,我们会遇到各种可能,比如下图右所示的情况:一开始车在停车位的右侧,且车头和停车位平行(例如侧位停车)。由于汽车都有一个最小转向半径,所以你不能让汽车像螃蟹一样横着开进去,这时求最短路径可就没那么容易了。图中汽车运动形成的黑色曲线就是Reeds-Shepp曲线。Reeds-Shepp曲线由几段半径固定的圆弧和一段直线段拼接组成,而且圆弧的半径就是汽车的最小转向半径。这里的路径长度是指汽车中心运动轨迹的长度,也就是所有圆弧的弧长和直线段的长度之和。
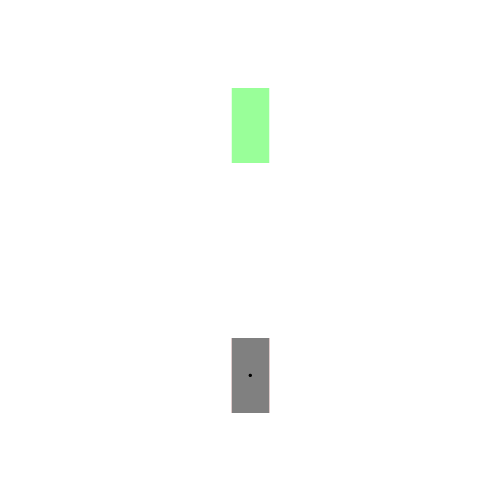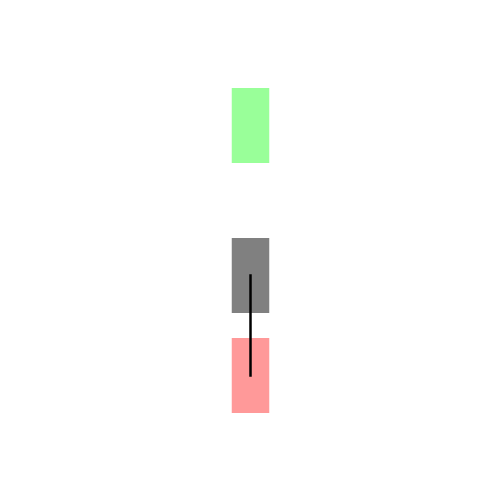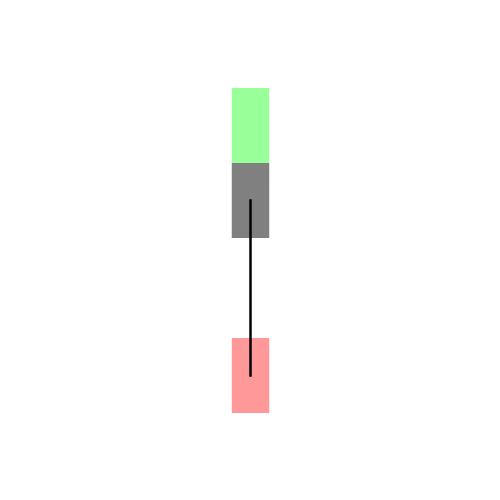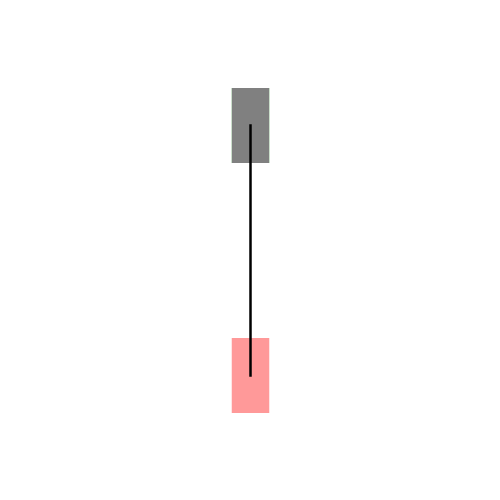
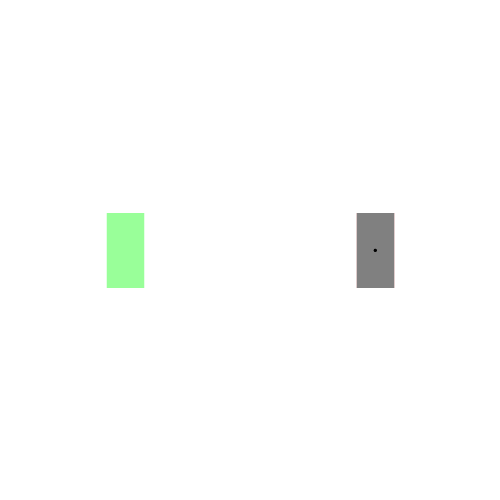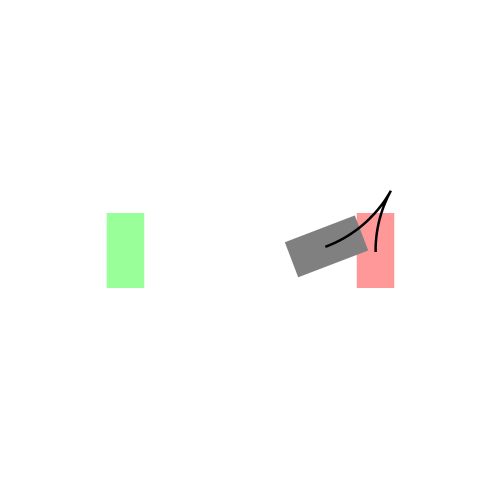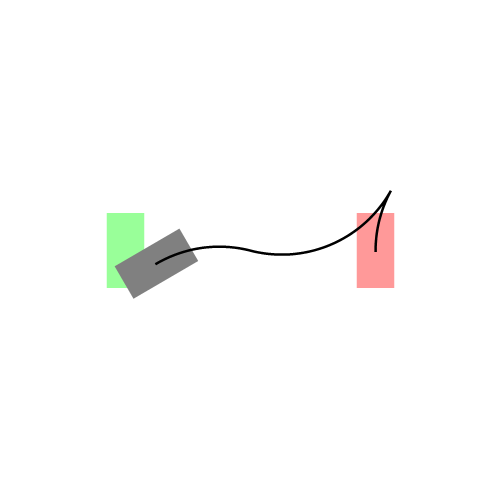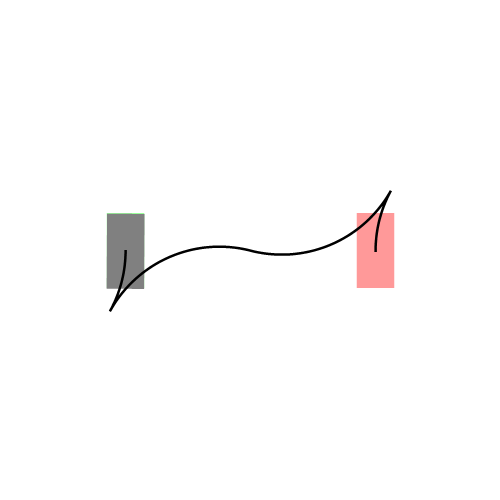
下图展示了更一般的情况,汽车从不同的初始位置和朝向进入同一个停车位:
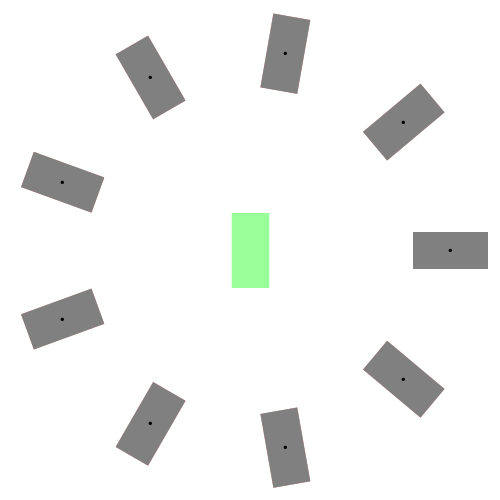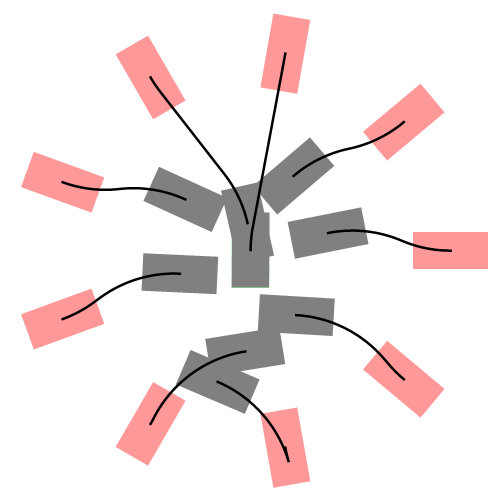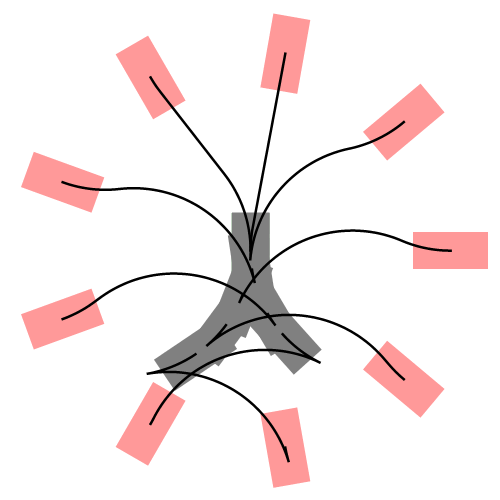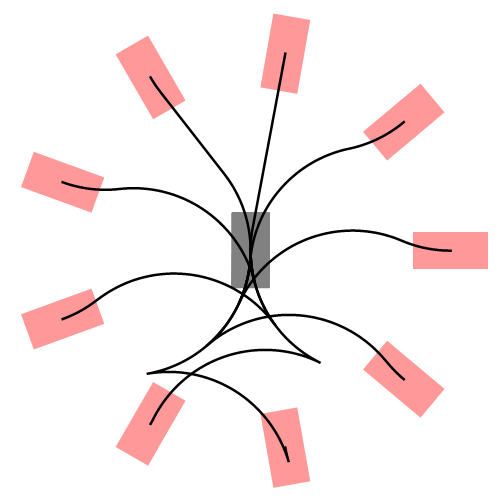
什么是Dubins曲线?
Dubins曲线和Reeds-Shepp曲线差不多,只不过多了一个约束条件:汽车只能朝前开,不能后退(不能挂倒挡)。Dubin
这篇关于Reeds-Shepp和Dubins曲线简介的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



