【深蓝学院】手写VIO第4章--基于滑动窗口算法的 VIO 系统：可观性和一致性--作业

本文主要是介绍【深蓝学院】手写VIO第4章--基于滑动窗口算法的 VIO 系统：可观性和一致性--作业，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 内容

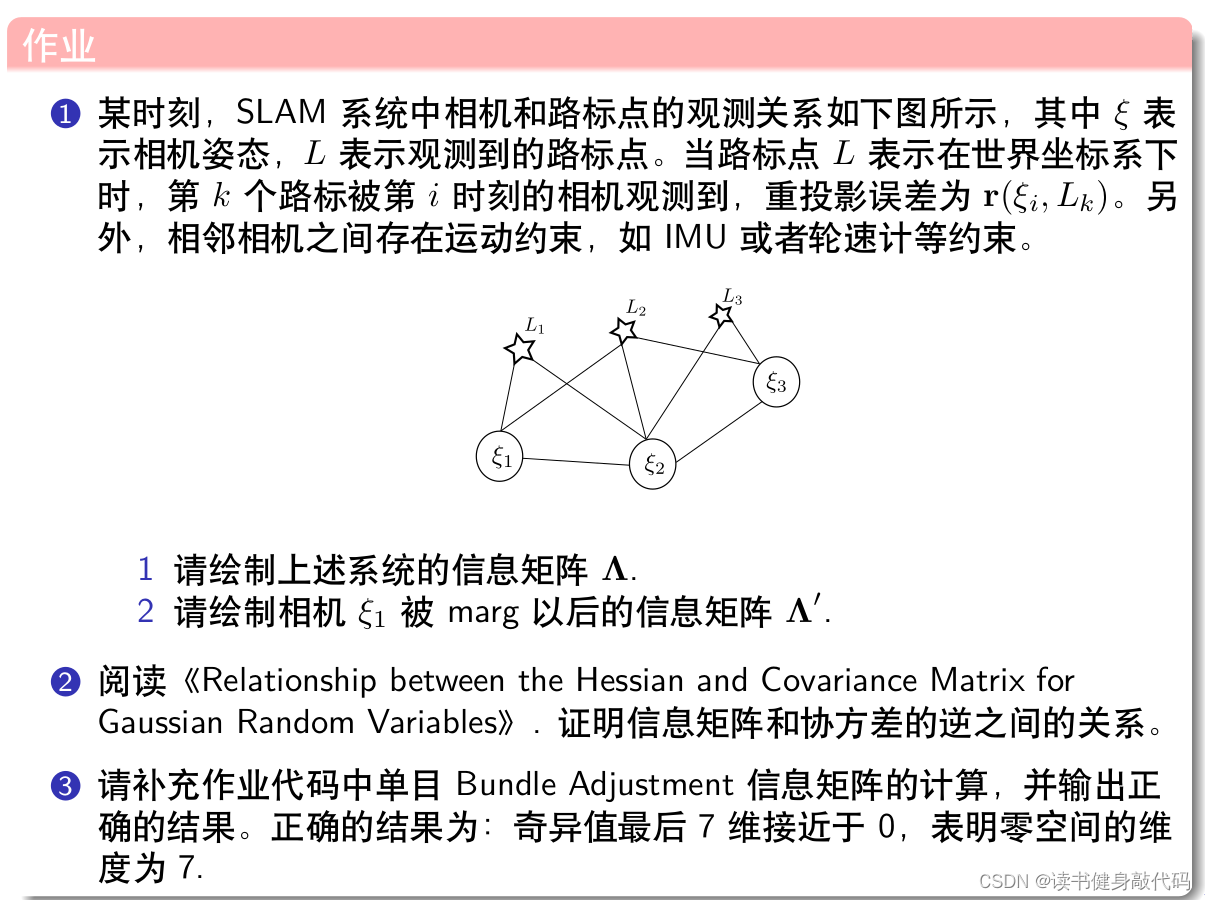
在这里插入图片描述

T1.

参考SLAM14讲P247直接可写，注意 $\xi_1,\xi_2$ 之间有约束（关系）。
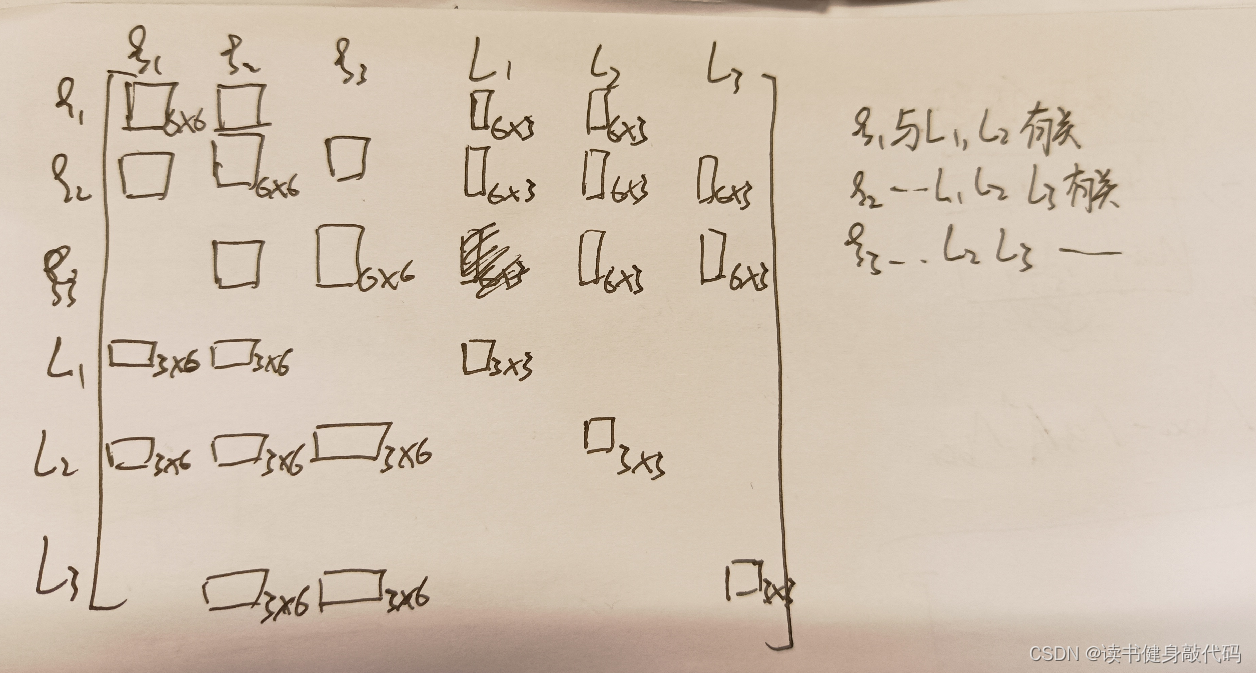
在这里插入图片描述

套用舒尔补公式：
marg掉 $\xi_1$ 之后，信息被传递到 $L_1和L_2$ 之间了。
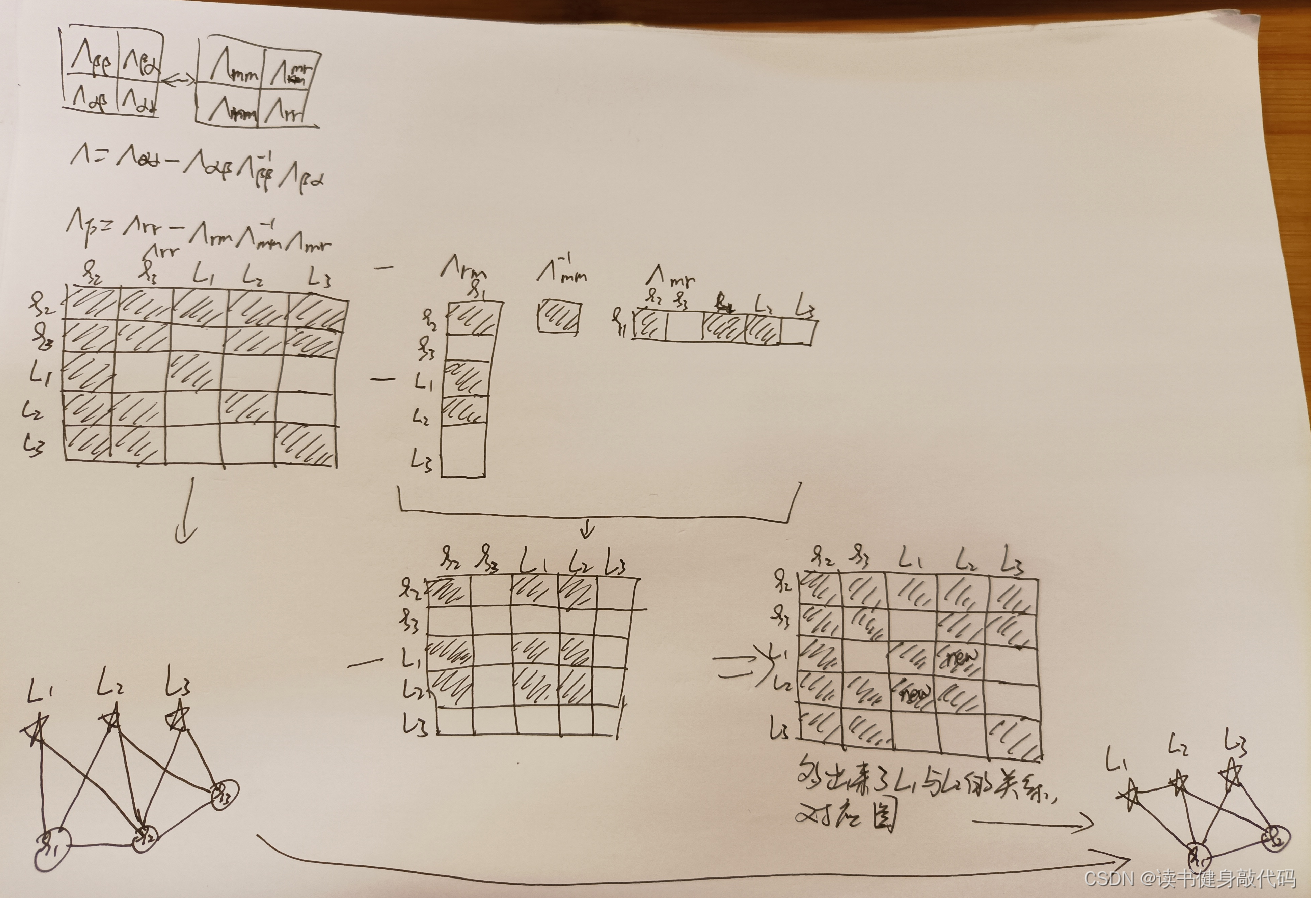
在这里插入图片描述

T2.

T3.

课上同学的作业分享：
在这里插入图片描述

在这里插入图片描述

算是勉强看着答案做出来了：
在这里插入图片描述
1.

我的维度不对，H的分布就是先pose，再路标点，所以先计算完pose的Jacobian才能计算landmark的Jacobian

那个Jacobian看不懂怎么算的。

在这里插入图片描述

整体代码

//
// Created by hyj on 18-11-11.
//
#include <iostream>
#include <vector>
#include <random>  
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>struct Pose
{Pose(Eigen::Matrix3d R, Eigen::Vector3d t):Rwc(R),qwc(R),twc(t) {};Eigen::Matrix3d Rwc;Eigen::Quaterniond qwc;Eigen::Vector3d twc;
};
int main()
{int featureNums = 20;int poseNums = 10;int diem = poseNums * 6 + featureNums * 3;double fx = 1.;double fy = 1.;Eigen::MatrixXd H(diem,diem);H.setZero();std::vector<Pose> camera_pose;double radius = 8;for(int n = 0; n < poseNums; ++n ) {double theta = n * 2 * M_PI / ( poseNums * 4); // 1/4 圆弧// 绕 z轴 旋转Eigen::Matrix3d R;R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));camera_pose.push_back(Pose(R,t));}// 随机数生成三维特征点std::default_random_engine generator;std::vector<Eigen::Vector3d> points;for(int j = 0; j < featureNums; ++j){std::uniform_real_distribution<double> xy_rand(-4, 4.0);std::uniform_real_distribution<double> z_rand(8., 10.);double tx = xy_rand(generator);double ty = xy_rand(generator);double tz = z_rand(generator);Eigen::Vector3d Pw(tx, ty, tz);points.push_back(Pw);for (int i = 0; i < poseNums; ++i) {Eigen::Matrix3d Rcw = camera_pose[i].Rwc.transpose();Eigen::Vector3d Pc = Rcw * (Pw - camera_pose[i].twc);double x = Pc.x();double y = Pc.y();double z = Pc.z();double z_2 = z * z;Eigen::Matrix<double,2,3> jacobian_uv_Pc;// Jacobian of residual with respect to point in camera coordinatejacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,0, fy/z, -y * fy/z_2;Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw;Eigen::Matrix<double,2,6> jacobian_Ti;jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,-(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2;H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;//guan yu pose de Jacobian/// 请补充完整作业信息矩阵块的计算//zhu dui jiao xian 3*3
//            H.block(i * 6 + j * 3,i * 6 + j * 3,3,3) += jacobian_Pj.transpose() * jacobian_Pj; //mine
//            H.block(i * 6 ,i * 6 + j * 3,6,3) += jacobian_Ti.transpose() * jacobian_Pj;
//            H.block(i * 6 + j * 3, i * 6 ,3,6) += jacobian_Pj.transpose() * jacobian_Ti;//zheng que deH.block(poseNums * 6 + j * 3,poseNums * 6 + j * 3,3,3) += jacobian_Pj.transpose() * jacobian_Pj;H.block(i * 6 ,poseNums * 6 + j * 3,6,3) += jacobian_Ti.transpose() * jacobian_Pj;H.block(poseNums * 6 + j * 3, i * 6 ,3,6) += jacobian_Pj.transpose() * jacobian_Ti;}}//    std::cout << H << std::endl;
//    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(H);
//    std::cout << saes.eigenvalues() <<std::endl;Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);std::cout << svd.singularValues() <<std::endl;return 0;
}