Python数据结构与算法-RAS算法（p96）

一、RSA加密算法简介

1、加密算法概念

• 传统密码: 加密算法是秘密的

• 现代密码系统:加密算法是公开的，密钥是秘密的；（密钥可能是随机生成的，与他人不一致）

• 对称加密—加密和解密用的同一个密钥

• 非对称加密—加密和解密用的两个密钥，RSA算法属于非对称加密

2、RSA加密算法

• RSA非对称加密系统:

• 公钥:用来加密，是公开的 （一般用来加密）

• 私钥:用来解密，是私有的 （个人用于解密）

• 例如：

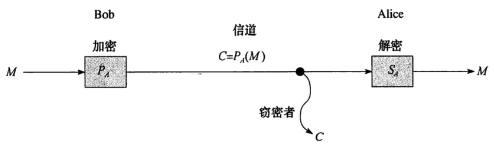
上图所示，Bob用公钥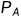加密M文件，Bob传送给Alice。传送过程中，窃密者窃取M文件得到的加密后的信息，无法解读。Alice使用私钥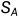解读M文件。

二、RSA算法的加密过程

1、RSA加密算法密钥获取过程

• 随机选取两个质数p和q；

• 计算n=pq

• 选取一个与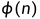互质的小奇数e,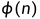=(p-1)(q-1)

• 对模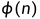,计算e的乘法逆元d，即满足(e*d) mod 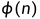= 1

• 公钥(e,n) 私钥(d, n)

2、RSA加密算法密钥获取演示

（1）随机选取两个质数p和q；

质数是指约数只有1和本身的数。

质数越大，密码破解难度越大，实际中的质数是很大的。

>>> p = 53
>>> q = 59

（2）计算n=pq

>>> n = p*q
>>> n
3127

（3）选取一个与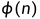互质的小奇数e,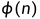=(p-1)(q-1)

互质是指最大公约数为1，奇数是与偶数相对的数，不能被2整除。

>>> fai = (p-1)*(q-1) #fai(n)
>>> fai
301
>>> e = 3

（4）对模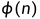,计算e的乘法逆元d，即满足(e*d) mod 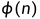= 1

找到一个d，满足（e * d） mod 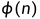= 1。（可运用费马小定理，欧几里得算法求解）

>>> d = 2011 # 这里对应的d是2011，可用费马定理求解（具体求解可自行学习）
>>> (e * d) % fai
1

（5）公钥(e,n) 私钥(d, n)

>>> e
3
>>> n
3127
>>> d
2011

公钥：(3, 3127); 私钥（2011,3027）

3、加密解码过程

• 加密过程: c=(m^e)mod n （公钥）

• c：密文

• m：明文

• n^e: n的e次方，在python中是n ** e

• 解密过程: m =(c^d)mod n （密钥）

（1）加密过程（终端运行）

>>> m = 87 # 明文
>>> c = (m ** e)%n # 加密
>>> c # 密文
1833

（2）解密过程（终端运行）

>>> (c ** d)%n
87 # 明文

三、RSA加密算法中求乘法逆元

1、乘法逆元定理

由于除法无法直接求模，转化为乘法再求模。

例如：

• 普通除法下： 14 / 4 = 7 / 2 = 7 x 1/2 = 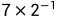,将除法转化为乘法。

• 在该式子下再取模就是模的除法：（14 / 4）mod 5 = (7 x 1/2) mod 5 =(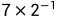) mod 5

• 乘法逆元类似与倒数的概念，两数相乘1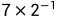，() mod 5 中取模的数一定为整数，所以1/2需要被整数替换。

• 因为(2 * 3) mod 5 =1, 则2对与mod 5的乘法逆元为3。可以用3替换1/2

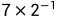• () mod 5 = (7 x 3) mod 5 =21 mod 5 = 1。理解为，7乘以“2的乘法逆元”模5。

乘法逆元定义：设a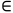Z， n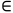N， 如果az 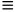1 (mod n) ,称z是模n下a的乘法逆元，记作。

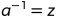其中： a的乘法逆元是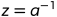，z的乘法逆元。

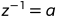注意1：模n下互为乘法逆元，一般只考虑比n小的数。

注意2：a在模n内的乘法逆元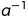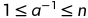（）是唯一的。也可能就是本身。

注意3：乘法逆元存在条件：gcd(a,n) = 1（最大公约数） ,即模n下，a有乘法逆元。也就是说a 和n互质。

2、用扩展欧几里得算法求乘法逆元

（1）扩展欧几里得算法

给出正整数a和b，扩展的欧几里得算法可以计算a和b的最大公约数d，同时得到两个符号相反的整数x和y满足：d=gcd(a, b) = ax+by。

（2）根据扩展欧几里得算法求乘法逆元

az 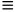1 (mod n) 求模的乘法逆元，又可以写成（a * z）mod n = 1,其中a和n互为质数，gcd(a,n)=1。

（可以得到a * z= y * n +1,这里的y是求解（a * z）mod n = 1中的系数。例如：（7 * 8）mod 11 =1，计算过程，7 * 8 = 5 * 11 + 1，这里的y是5。）

根据扩展欧几里得算法，即得到ax + by = gcd(a, b) = 1。整个求解的过程就是使用欧几里得算法gcd(a,b) = gcd(b, a mod b)，求两个数的公约数，一直计算到1为止即可。例如：

• a = 5，b = 14

14 % 5 =14 - 5 * 2 = 4

5 % 4 = 5 - 4 * 1 = 1 = gcd(a,b)

往回推算：4 = 14 - 5 * 2 替换

5 - (14 - 5* 2) = 1

5 - 14* 1+ 5* 2 =1

5*3 - 14*1 =1

此时x=3，y =1。但是y不是所求的。

则3 是 5 mod 14 的逆元。

• 当由于式子是奇数个，所以最后整理时a的系数为负：

a =5, b = 18

18 % 5 = 18 - 5 * 3 = 3

5 % 3 = 5 - 3*1 = 2

3 % 2 = 3 - 2 * 1 =1

倒回去：

3-（5 - 3 * 1）=1

18 - 5 * 3 -（5 - 18 + 5 * 3）= 18 - 5 * 3 -5 * 4 + 18 = 18 * 2 - 5 * 7=1

转化为5*（-7）+ 18 * 2 = 1

利用两个数互质的性质以及最小公倍数，我们可以直接得到想要的结果：

5*（-7）+ 18 * 2 = 5 * （-7） mod 18 = 5 * （18-7）mod 18 = 5 * 11 mod 18 =1

最终x= 11.

(欧几里得算法求逆元的代码实现暂时略)