本文主要是介绍《数据结构-用C语言描述第三版》课后答案 第五章，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
撰写匆忙，如有错误，尽情指正
1．选择题
(1）设有一个二维数组 A [ m ][ n ]，假设 A [0][0］存放地址为644, A [2][2］存放地址为676，每个元素占一个空间，则 A [3][3］的存放地址为（)。
A .688
B .678
C .692
D .696
答：
A[2][2]的地址等于 (2*n+2)*1 +644 = 676 则n = 15
则A[3][3]的地址等于 （3*n+3)*1+644 = 48+644 = 692
(2）设有一个10阶的下三角矩阵 A （包括对角线），按照从上到下、从左到右的顺序存储到55个连续的存储单元中，每个数组元素占1个字节的存储空间，则 A [5][4］的地址与 A [0][0］的地址之差为（)
A .10
B .19
C .28
D .55
答：
设A[0][0]的地址为 0
则 到A[5][4]总共有1+2+3+4+5+5 = 20个元素，则 A[5][4]的地址为19+0 = 19
即地址之差为19
2．设有一个上三角矩阵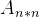 
，将其上三角中的元素逐列压缩存储到一个大小为 n ( n +1)/2的一维数组 C 中（下标从1开始），请给出计算上三角矩阵中任意元素 a ( i < j ）在一维数组 C 中位置的公式。
答:
计算上三角矩阵中前（j-1）列非零元素个数
为第j列第i个元素，则
个元素
即C[
注：此类题即求元素按照要求压缩存储时第k个元素和i,j的关系，用i，j表示k，找出规律即可
3．设有三对角矩阵 A 将其三条对角线上的元素逐行压缩存储到一个大小为3n-2的一维数组 B 中（下标从1开始），使得 B [ k ]= a ，求：
(1）用 i , j 表示 k 的下标变换公式；
(2）用 k 表示 i , j 的下标变换公式。
答：
（1）此问为三对角矩阵的逐行压缩，同样是计算第k个元素的i,j表示
分类讨论：
i = 1时，k = j
i > 1时，k = 前i-1行元素个数+
即k =
=
公式中：
为前i-1行元素个数
为第i行第几个元素，这个应该也很好理解，第i行三个非零元素中，第二个元素下标i和j相等，第一个元素和第三个元素i,j相差1
则
（2）此问已知k求i、j，反过来求解即可
当k<=2时
i = 1, j = k;
当k>2时
可以知道，k有三种取值
、
、
，显然k和i之间有k除以3后取整的关系
i =
j =
综上：
4．一 n 阶对称矩阵 A 以行序为主序压缩存储在一维数组 B 中，存储其下三角元素（包括对角线），计算 A [i][j]与 B[k] 之间的对应关系。
答：
关键字：n阶对称矩阵，行序存储，存储下三角
则i<=j时,按照下三角矩阵压缩存储下标计算方式
k =
i>j时，互换i、j即可
则A[i][j]与k的对照关系
k =
5．在算法5.3（稀疏矩阵一次定位快速转置算法）中，将计算 position [ col ］的方法稍加改动，使算法只占用一个辅助向量空间
答：
在稀疏矩阵的一次定位快速转置算法中，有两个辅助向量空间，分别为num[],position[]
其中num[]记录每列非零元素个数，用于position[col]的计算，position[col]代表col列第一个元素在三元组表中的位置，具体算法可以查看课本
现在改动position[col]的计算方法，即利用position[]自己计算最终的position[]
//原算法 int num[MAXSIZE],position[MAXSIZE];for(t=1,t<=A.len;t++){//遍历三元组表计算每列非零元素个数num[A.data[t].col]++; } position[1] = 1; for(col=2;col<=A.n;col++){position[col] = position[col-1] + num[col-1]; //即col列首个元素位置等于col-1列首个元素位置加col-1列非零元素个数 }//算法改进 //上述position[0]未使用，因此可以加以利用 //同样，计算每列非零元素个数 int position[MAXSIZE]; for(t=1,t<=A.len;t++){//遍历三元组表计算每列非零元素个数position[A.data[t].col]++; }position[0] = position[1]; position[1] = 1; for(col=2;col<=A.n;col++){int temp = position[col]; //记录col列元素非零个数position[col] = position[col-1] + position[0]; position[0] = temp; //即col列首个元素位置等于col-1列首个元素位置加col-1列非零元素个数 }
6．编写算法，实现三元组表表示的两个稀疏矩阵的加法。
答：
在三元组表表示中，稀疏矩阵元素按照列优先依次排列，此时遍历两个稀疏矩阵分别判断是否为同行同列然后进行相应操作即可
若为同行同列，则元素相加，若不为同行同列，则添加非零元素，此时新开辟结果空间（有时候浪费空间的做法能很好的解决问题，不一定非要进行原地操作）
具体见代码
//三元组表的定义
#define MAXSIZE 1000
typedef struct {int i,j;ElementType elem;
}Triple;typedef struct{Triple data[MAXSIZE];int m,n,len;
}TSMatrix;TSMatrix matrixAdd(TSMatrix A,TSMAtrix B){TSMatrix C;//使用双指针遍历两个矩阵int i=1, j=1;int k = 1;while(i<=A.len && j<=B.len){//分三种情况，情况分类的依据：i指向的元素在矩阵的位置位于j指向元素的相对位置//情况1： i指向元素在j指向元素的前面，则将i指向元素复制给结果三元组表 i++//情况2： i指向元素和j指向元素位置一样，则将两元素相加后复制给结果三元组表 i++, j++//情况3： i指向元素在j指向元素的后面，则将j指向元素复制给结果三元组表 j++if[A.date[i].i<B.date[j].i]{//情况1C.date[k] = A.date[i];k++,i++;}else if(A[i].i = B[j].i){if(A.date[i].j < B.date[j].j){//情况1C.date[k] = A.date[i];k++,i++;}if(A.date[i].j = B.date[j].j){//情况2C.date[k] = A.date[i];C.date[k].elem += B.date[j].elem;k++,i++,j++;}if(A.date[i].j > B.date[j].j){//情况3C.date[k] = A.date[j];k++,j++;}}else{//情况3C.date[k] = B.date[j];k++,j++;}}while(i<=A.len){C.date[k] = A.date[i];k++,i++;}while(j<=B.len){C.date[k] = B.date[j];k++,j++;}C.m = A.m;C.n = A.n;C.len = k-1;
}7．编写算法，实现一个在十字链表中删除非零元素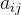 
。
答：
看见十字链就头疼🥱🥱🥱
十字链表表示法对于机器是十分友好的，但是对于我们来说，也许并不是很难，但是箭头指来指去的也是让人望而生畏
直接遍历十字链表的行表头指针和列表头指针找到要删除元素的位置然后修改指针指向释放要删除指针即可
//十字链表定义, 同课本（从课本上抄来的）
typedef struct OLNode {int row,col;ElementType elem;struct OLNode *right,*left;
}OLNode; *OLink;typedef struct {OLink *row_head, *col_head;int m,n,len;
}Crosslist;void funcdelete(Crosslist *cl,OLNode aij){// cl要操作的十字链表 aij 要删除的非零元素//此处省略aij元素的合法性判断， //找到要删除元素所在行表头和列表头OLNode *rh = cl->row_head[aij.row];OLNode *ch = cl->col_head[aij.col];//根据表头定位到要删除元素while(rh->right->col<aij.col){ //定位到row行col列rh = rh->right;}while(ch->down->row<aij.row){ //定位到col行row列ch = ch->down;}//删除当前元素//首先记录要删除元素OLNode * temp = rh->right;//改变指向该元素的指针rh->right = temp->right;ch->down = temp->down;free(temp);
}
8．画出下列广义表的两种存储结构图示：
(((( a ),b)),(((), d ),( e , f)))
答：
考点总结：
广义的表的存储结构：
头尾链表存储结构：表节点和原子结点组成，将表依次拆解为表头和表尾之后链接即可
同层结点链式存储结构：实际上类似顺序表的链式存储
头尾链表存储结构图示
同层结点链式存储图示
9．求下列广义表运算的结果：
(1) Head [(( a , b ),( c , d ))];
答：( a , b )
(2) Tail [(( a , b ),( c , d ))];
答：( c , d )
(3) Tail [ Head [(( a , b ),( c , d ))]];
答：b
(4) Head [ Tail [ Head [(( a , b ),( c , d ))]]]；
答：b
(5) Tail [ Head [ Tail [(( a , b ),( c , d ))]]];
答：[]
10．广义表 A =( a , b ,( c , d ),( e ,( f , g )))，则 Head ( Tail ( Head ( Tail ( Tail ( A ))))）的值为（D）
A .( g )。
B .( d )
C . c
D . d
答：
Tail(A) = (b ,( c , d ),( e ,( f , g )))
Tail ( Tail ( A )) = (( c , d ),( e ,( f , g )))
Head ( Tail ( Tail ( A ))) = (c , d )
Tail ( Head ( Tail ( Tail ( A )))) = (d)
Head ( Tail ( Head ( Tail ( Tail ( A ))))） = d
这篇关于《数据结构-用C语言描述第三版》课后答案 第五章的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
