本文主要是介绍lsd:tracking,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
SE(3) Tracking new frame:
新图像与模板图像在映射后的光度残差表达式:
rp(x,ξji)=Ii(x)−Ij(ω(x,Di(x),ξji))
其中j是新图像帧,i是关键图像帧。forward additive的光度残差对迭代增量 Δξ 求导得:
JΔξ=∇I|ω(x,(T)∂π∂p′∣∣∣Tp.∂p′∂T∣∣∣ΔTTi.∂T∂ΔT∣∣∣I.∂exp(Δξ^)∂Δξ∣∣∣0.
其中:
∇I|ω(x,T)=(ΔIuΔIv) :模板图像上像素坐标 x(u,v) 在T进行warp后得到的新图像 I′ 中像素坐标 x′(u′,v′) 的梯度.
∂π∂p′∣∣∣Tp.=⎛⎝⎜⎜fx1z′00fy1z′−fxx′z′2−fyy′z′2⎞⎠⎟⎟ :针孔相机模型求导。
这里令 Ti=⎛⎝⎜⎜⎜⎜r11r21r310r12r22r320r13r23r330txtytz1⎞⎠⎟⎟⎟⎟ , p′=Tip , 所以有:
∂p′∂T∣∣∣ΔTTi.∂T∂ΔT∣∣∣I.∂exp(Δξ^)∂Δξ∣∣∣0.=⎛⎝⎜⎜x000x000xy000y000yz000z000z100010001⎞⎠⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜r1100r1200r1300tx000r1100r1200r1300tx000r1100r1200r1300txr2100r2200r2300ty000r2100r2200r2300ty000r2100r2200r2300tyr3100r3200r3300tz000r3100r3200r3300tz000r3100r3200r3300tz000000000100000000000010000000000001⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜0000000001000000000000100000000000010000010−1000000−1000100000010−100000000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
注意上面的表达式中在迭代过程中, ∂p′∂T∣∣∣ΔTTi. 和 ∂exp(Δξ^)∂Δξ∣∣∣0. 是始终不变的。但是 ∇I|ω(x,T) 、 ∂π∂p′∣∣∣Tp. 和 ∂T∂ΔT∣∣∣I. 每次迭代都是不一样的。由 Ti 的表达式可知:
⎧⎩⎨x′=r11x+r12y+r13z+txy′=r21x+r22y+r23z+tyz′=r31x+r32y+r33z+tz
所以:
∂p′∂T∣∣∣ΔTTi.∂T∂ΔT∣∣∣I.= ⎛⎝⎜⎜x′000x′000x′y′000y′000y′z′000z′000z′100010001⎞⎠⎟⎟
exp(Δξ^)=(e[ω]×0Vv1)
其中:
[ω]×=⎛⎝⎜0ω3−ω2−ω30ω1ω2−ω10⎞⎠⎟;v=⎛⎝⎜v1v2v3⎞⎠⎟
e[ω]×V=I+sin(||ω||)||ω||[ω]×+1−cos(||ω||)||ω||2[ω]2×=I+1−cos(||ω||)||ω||2[ω]×+||ω||−sin(||ω||)||ω||3[ω]2×
上式在 ||ω||=0 附近,对 sin(||ω||) 和 cos(||ω||) 进行一阶泰勒展开得:
e[ω]×V≈I+12[ω]×+16[ω]2×≈I+[ω]×+12[ω]2×
所以矩阵求导得:
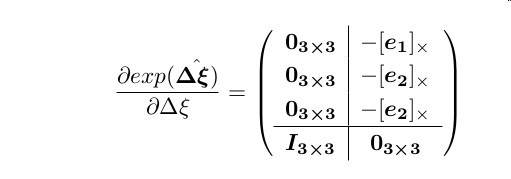
其中 e1=[1,0,0]T , e2=[0,1,0]T , e1=[0,0,1]T .
JΔξ===(∇Iu∇Iv)T⎛⎝⎜⎜fx1z′00fy1z′−fxx′z′2−fyy′z′2⎞⎠⎟⎟⎛⎝⎜⎜x′000x′000x′y′000y′000y′z′000z′000z′100010001⎞⎠⎟⎟⎛⎝⎜⎜⎜⎜03×303×303×3I3×3−[e1]×−[e2]×−[e2]×03×3⎞⎠⎟⎟⎟⎟(∇Iu∇Iv)⎛⎝⎜⎜fx1z′00fy1z′−fxx′z′2−fyy′z′2⎞⎠⎟⎟⎛⎝⎜⎜1000100010−zy′z′0−x′−y′x′0⎞⎠⎟⎟1z′(∇Iufx∇Ivfy)T⎛⎝⎜⎜⎜1001−x′z′−y′z′−x′y′z′−(z′+y′2z′)z′+x′2z′x′y′z′−y′x′⎞⎠⎟⎟⎟
注意:forward additive的本质是将第一幅图像向第二幅图像warp后,比较warp得到的图像和第二幅图像之间的残差。在迭代过程中,warp后图像的像素坐标 (u′,v′) ,点坐标 (x′,y′,z′) 需要每次都重新求。
光度残差协方差的来源分别为:模板图像光度协方差、新图像光度协方差、逆深度估计引起的模板光度协方差。根据残差协方差传播的方程:
ΣI≈JΣDTJT ,\和函数: I(ω(x,DT(X),T))=I(π(Tπ−1(x,1DT(x)))) ,所以光度对逆深度的求导为:
∂rp(T)∂DT=∇I|ω(x,Ti)∂π∂p′∣∣∣Tip.∂p′∂p∣∣∣p.∂π−1∂Z∣∣∣1DT(x).∂1x∂x∣∣∣∣∣DT(x).
其中:

因为 {ππ−1:(u,v)=Kp:p=K−1(u,v) ,所以有 ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x=z(u−cx)fxy=z(u−cy)fyz=z ,
因而:
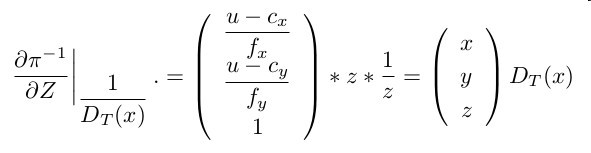
该导数化简为:
∂rp(T)∂DT====∇I|ω(x,Ti)∂π∂p′∣∣∣Tip.∂p′∂p∣∣∣p.∂π−1∂Z∣∣∣1DT(x).∂1x∂x∣∣∣∣∣DT(x).(∇Iu∇Iv)⎛⎝⎜⎜fx1z′00fy1z′−fxx′z′2−fyy′z′2⎞⎠⎟⎟⎛⎝⎜r11r21r31r12r22r32r13r23r33⎞⎠⎟⎛⎝⎜xyz⎞⎠⎟DT(x)−1DT(x)2(∇Iu∇Iv)T⎛⎝⎜⎜fx1z′00fy1z′−fxx′z′2−fyy′z′2⎞⎠⎟⎟⎛⎝⎜x′−txy′−tyz′−tz⎞⎠⎟1DT(x)1DT(x)z′2(∇Iufx(txz′−tzx′)+∇Ivfy(tyz′−tzy′))
综上,光度残差的协方差计算公式是:
σ2rp(T)==σ2I+σ2J+(∂rp(T)∂DT)2σ2DT2σ2I+(∂rp(T)∂DT)2VDT
Sim(3) Tracking keyframe:
当新选定一帧图像作为关键帧时,就会依据以前关键帧对新选择的关键帧上某些像素位置的深度给出估计。有了深度估计后,考虑tracking时会考虑两幅图像的光度匹配残差和新图像深度估计与warp后深度的深度残差。使用这两个残差去驱动求解、修正这两个关键帧之间的位姿变换。\
首先看下残差代价函数:
E(T):=∑x∈ΩDT[αx(T)σ2rp,x(T)r2p,x(T)+αx(T)σ2rd,x(T)r2d,x(T)]
其中:
rp,x(T)rd,x(T)αxσ2rp,x(T)σ2rd,x(T):=IT(x)−II([x′]1,2):=[x′]3−DI([x′]1,2):=ρδ(r2p,x(T)σ2rp,x(T)+r2d,x(T)σ2rd,x(T)):=2σ2I+(∂rp,x(T)∂DT(x)∣∣∣DT(x).)2VDT(x):=(∂rd,x(T)∂DI∣∣∣DI([x′]1,2).)2VI([x′]1,2)+(∂rd,x(T)∂DT(x)∣∣∣DT(x).)2VDT(x)
其中 x′=ωs(x,DT(x),T) 表示变换和映射过后的点,前两个坐标是其在新图像中的像素坐标,第三个是其深度值。 ρδ 是huber加权的权重函数。\
下面来看下 光度残差函数对于变换增量的导数:
Jp,x=∇I|ω(x,T)∂π∂p′∣∣∣Tp.∂p′∂T∣∣∣ΔTTi.∂T∂ΔT∣∣∣I.∂exp(Δξ^)∂Δξ∣∣∣0.
上式与SE(3)中等式唯一的不同是 ξ 有7个变量,增加了变量s,其他表达式不变,但:
∂exp(Δξ^)∂Δξ∣∣∣0.=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜0000000001000000000000100000000000010000010−1000000−1000100000010−100000000100010001000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
与前面的计算过程一样,经过化简后得到:
Jp,x=1z′(∇Iufx∇Ivfy)T⎛⎝⎜⎜⎜1001−x′z′−y′z′−x′y′z′−(z′+y′2z′)z′+x′2z′x′y′z′−y′x′00⎞⎠⎟⎟⎟
光度残差函数度对于逆深度的导数与SE(3)一样:
∂rp,x(T)∂DT=1DT(x)z′2(∇Iufx(txz′−tzx′)+∇Ivfy(tyz′−tzy′))
深度残差对于增量位姿变换的导数:
Jd,x=(∂πz∂p′∣∣∣Tp.−∇D|ω(x,Ti)∂π∂p′∣∣∣Tp.)∂p′∂T∣∣∣ΔTTi.∂T∂ΔT∣∣∣I.∂exp(Δξ^)∂Δξ∣∣∣0.
其中:\
∂πz∂p′∣∣∣Tp.=∂1z′∂p′∣∣∣∣∣Tp.=(00−1z′2) \
基于性能原因,我们忽略 ∇D|ω(x,Ti)∂π∂p′∣∣∣Tp.
计算化简得:
Jd,x=(00−1z′2−y′z′2x′z′20−1z′)
深度残差对于新关键帧I逆深度的导数:
∂rd,x(T)∂DI∣∣∣DI([x′]1,2).=−1
深度残差对于模板关键帧T逆深度的导数:
∂rd,x(T)∂DT∣∣∣DT(x)=∂πz∂p′∣∣∣Tip.∂p′∂p∣∣∣p.∂π−1∂Z∣∣∣1DT(x).∂1D∂D∣∣∣∣∣DT(x)=⎛⎝⎜⎜⎜00−1z′2⎞⎠⎟⎟⎟T⎛⎝⎜r11r21r31r12r22r32r13r23r33⎞⎠⎟⎛⎝⎜xyz⎞⎠⎟DT(x)−1DT(x)2=(00−1z′2)⎛⎝⎜x′−txy′−tyz′−tz⎞⎠⎟1DT(x)=z′−tzDT(x)z′2
Storage Jacobian Parameter:
对于 sim(3) 的求解过程中的存储参数在这里介绍下,方便看懂作者的源代码。由于 Jp,x 在s上的导数始终为0,所以该雅可比仍然采用SE(3)的6参数格式。由于 Jd,x 只在4个位置上有数据,所以采用4参数存储格式。
由上一部分可知:
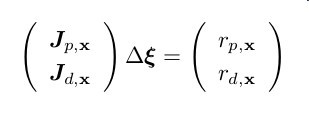
所以
Δξ=−[(Jp,xJd,x)(Jp,xJd,x)]−1(Jp,xJd,x)(rp,xrd,x)=−[JTp,xJp,x+JTd,xJd,x]−1[Jp,xrp,x+Jd,xrd,x]=−[Ap,x+Ad,x]−1[bp,x+bd,x]=−A−1b
其中
Ab=Ap,x+Ad,x=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜Ap,11Ap,21Ap,31Ap,41Ap,51Ap,610Ap,12Ap,22Ap,32Ap,42Ap,52Ap,620Ap,13Ap,23Ap,33Ap,43Ap,53Ap,630Ap,14Ap,24Ap,34Ap,44Ap,54Ap,640Ap,15Ap,25Ap,35Ap,45Ap,55Ap,650Ap,16Ap,26Ap,36Ap,46Ap,56Ap,6600000000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜0000000000000000Ad,11Ad,21Ad,310Ad,4100Ad,12Ad,22Ad,320Ad,4200Ad,13Ad,23Ad,330Ad,43000000000Ad,14Ad,24Ad,340Ad,44⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=bp,x+bd,x=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜bp1bp2bp3bp4bp5bp60⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜00bd1bd2bd30bd4⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
简单起见,这里没有考虑权重,但代码里是加了权重的。
Huber Weight Function:
huber函数的形式 αx:=ρδ(r2p,x(T)σ2rp,x(T)+r2d,x(T)σ2rd,x(T))
虽然写成这样,但真正的变量是: x=|rp,x(T)σrp,x(T)|+|rd,x(T)σrd,x(T)| .
所以权重函数是:
αx=ω(x)=⎧⎩⎨1k|x||x|<=k|x|>=k
Affine Lighting Correction:
考虑光照变化的场景,建立了光照仿射模型:
rp,x(ξ)=aIT(x)+b−II(x′)
这里a,b可以消除场景光照变化引起的共性光度残差,而 ξ 可以消除由于几何运动引起的异性光度残差。引入a,b消除共性残差后,会使 ξ 对异性残差更为敏感,在较少的迭代次数内就能求出 ξ 的真值。
考虑a,b引起的共性残差的迭代最小化公式是:
Ea,b(a,b)=∑x∈ΩDTρa,b(aIT(x)+b−II(x′))
其中 ρa,b(r)=min{δmax,r2} .
关于a,b的值作者给出的封闭解是这样的:
⎧⎩⎨⎪⎪⎪⎪⎪⎪a∗b∗=∑x∈ΩLIT(x)II(x′)∑x∈ΩLII(x′)II(x′)=1|ΩL|∑i(IT(x′)−a∗II(x))
ΩL:={x∈ΩT|ρa,b(aIT(x)+b−II(x′))<δmax}
上面关于a,b应该是有错误的.
下面给出两种可能正确的解:
一、根据线性回归函数性质可知:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪a∗b∗=∑x∈ΩLIT(x)II(x′)−nIT(x¯¯¯¯¯¯¯)II(x′¯¯¯¯¯¯¯∑x∈ΩLIT(x′)IT(x′)−nIT(x′)¯¯¯¯¯¯¯¯¯2=1|ΩL|∑i(II(x′)−a∗IT(x))
二、依据源代码,提出a,b封闭解的一种可能假设。(仍然存在不足,仅供参考。)
给定一组样本 xi 和每个样本的权重 pi ,做如下简记:
⎧⎩⎨sxswsxx=∑xi⋅pi=∑pi=∑x2i⋅pi
则这组样本的平均值是: E(x)=∑xi⋅pi∑pi=sxsw
方差为:
D(x)=E[(x−E(x))2]=∑(xi−E(x))2⋅pi∑pi=∑x2i⋅pi−2E(x)∑xi⋅pi+E2(x)∑pisw=sxx−2E(x)sx+E2(x)swsw=sxxsw−2(sxsw)2+(sxsw)2=sxxsw−(sxsw)2
理想情况下有:
II(x′)=aIT(x)+b
根据上面的推导,令
D(II(x′))D(IT(x))=syysw−(sysw)2=sxxsw−(sxsw)2
由 D(II(x′))=a2⋅D(IT(x)) 得:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪a∗b∗=D(II(x′))D(IT(x))−−−−−−−−√=syysw−(sysw)2sxxsw−(sxsw)2−−−−−−−−−−−−⎷=syy−(sy)2swsxx−(sx)2sw−−−−−−−−−−−⎷=sysw−a∗⋅sxsw=sy−a∗⋅sxsw
这篇关于lsd:tracking的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


![[论文阅读笔记31] Object-Centric Multiple Object Tracking (ICCV2023)](https://img-blog.csdnimg.cn/direct/e45906a3acc34a5e9398ebc675fbd75e.png)