本文主要是介绍自动驾驶规划中使用 OSQP 进行二次规划 代码原理详细解读,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1 问题描述
什么是稀疏矩阵 CSC 形式
QP Path Planning 问题
1. Cost function
1.1 The first term:
1.2 The second term:
1.3 The thrid term:
1.4 The forth term:
对 Qx''' 矩阵公式的验证
整体 Q 矩阵(就是 P 矩阵,二次项的权重矩阵)
整体 P 矩阵的形式如下:
目标函数中的线性项部分,即 q 矩阵的构建
计算 q 矩阵的代码块如下:
2. Constraints
2.1 不等式约束
2.2 连续性约束
Equality constraints
不等式约束的上下边界条件为:
上下边界条件是如何计算的?
二阶导边界极值的计算:
三阶导边界极值的计算
最后,A 矩阵为:
仿射矩阵 A
1 问题描述
典型的优化问题可以用以下的数学表达式来描述:
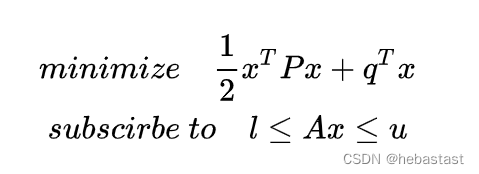

其中,P 是一个 n x n 的半正定矩阵, x 为 n 维向量,q 为 m x n 的矩阵。
需要注意的是,二次规划只在代价函数为凸函数的时候能够收敛到最优解,因此这需要 P 矩阵为半正定矩阵,这是非常重要的一个条件。这反映在 Apollo 中的规划算法则为需要进行求解的空间为凸空间,这样二次规划才能收敛到一条最优 Path。
上面的表述源自:Apollo 二次规划算法(piecewise jerk path optimizer)解析
什么是半正定矩阵?什么是正定矩阵?
设 A 为实对称矩阵,若对于每个非零实向量 X,都有 X'AX ≥ 0,则称 A 为半正定矩阵,称 X'AX 为半正定二次型。(其中,X'表示 X 的转置。)
注 :
在 OSQP 中,对上述的数据用结构体 OSQPData 进行封装,其定义如下:
// the location of file: /usr/local/include/osqp/types.h
typedef struct {
c_int n; ///< number of variables n
c_int m; ///< number of constraints m
csc *P; ///< the upper triangular part of the quadratic cost matrix P
csc *A; ///< linear constraints matrix A in csc format (size m x n)
c_float *q; ///< dense array for linear part of cost function (size n)
c_float *l; ///< dense array for lower bound (size m)
c_float *u; ///< dense array for upper bound (size m)
} OSQPData;
其中,P 和 A 都是以稀疏矩阵 CSC 的形式进行存储的。
什么是稀疏矩阵 CSC 形式
CSC - Compressed sparse column (CSC or CCS)
稀疏矩阵和稠密矩阵 - 看矩阵中非零元素占所有元素的比例
在矩阵中,若数值为 0 的元素数目远远多于非 0 元素的数目,并且非 0 元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非 0 元素数目占大多数时,则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。
稀疏矩阵的常规方式
下面是最常见的一种,也很好理解,(row,col) 指向矩阵非零元素的索引,data 里为该元素的值。
稀疏矩阵的 CSC 形式 - csc_matrix
按列压缩 Compressed sparse column,顾名思义将每一列出现的非零元素的个数统计后放好。
如何保证规划算法求解的空间为凸空间?
QP Path Planning 问题
QP 问题的标准形式(下面是常见的两种表示方法):
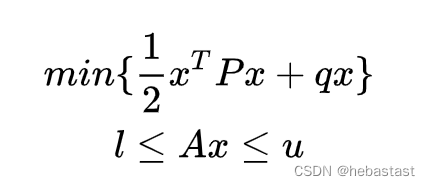


1. Cost function
论文中的 cost 函数实际上是如下的形式:

优化变量的形式是:
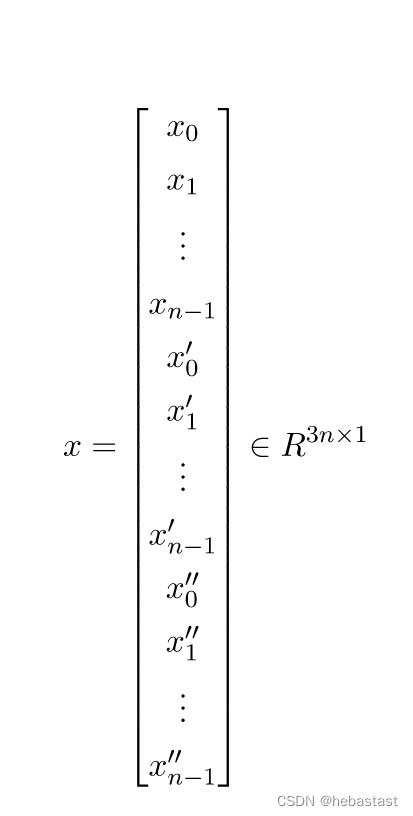
Cost function 也可以写成下面这种形式:

我们注意到第一项和第二项的内容似乎相同,但其实是有所区别的。我们通过下图来解释。

可以看到,我们要规划的离散点曲线是在 SL 坐标系下进行的。所以第一项惩罚的横向偏移也就是偏移 s 的法向的距离,可以理解为关于车道中心线的偏移。而第四项关于参考线的偏移,则是考虑了静态和低速障碍物生成的一条参考线,第四项所计算的偏移其实是关于参考线的偏移。我们可以这样理解这两项:我们规划的最优轨迹要尽量贴合原来的车道中心线,同时还要尽量贴合能够避障的参考线。
1.1 The first term:
一共有 n 个点:

假如有四个点需要优化,为 x0, x1, ... x3,则矩阵为:
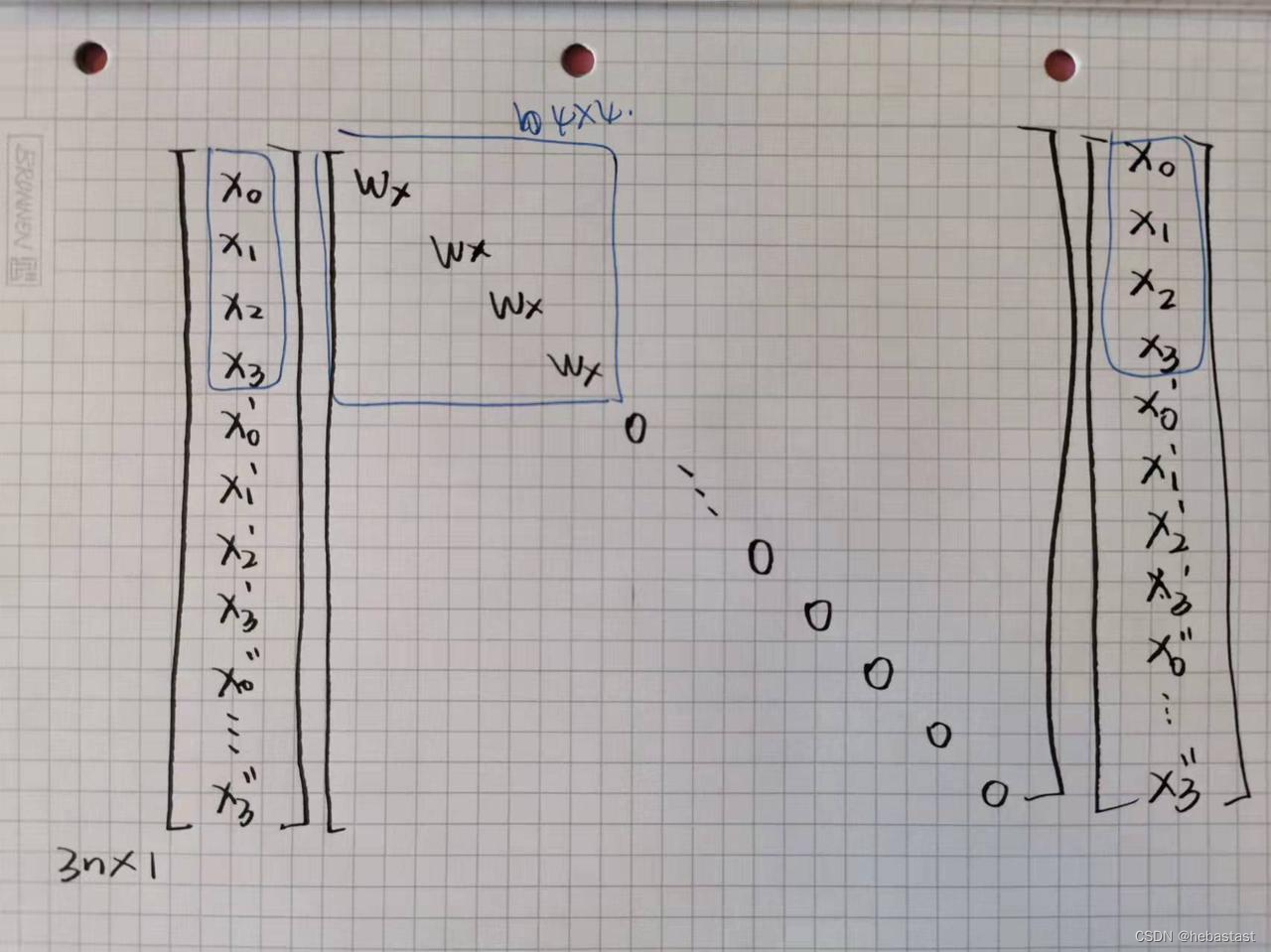
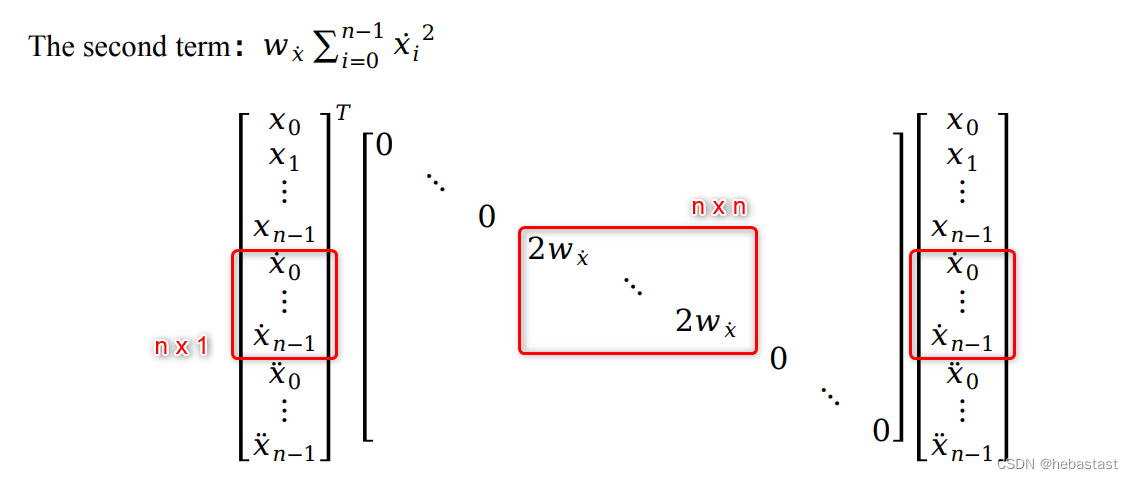
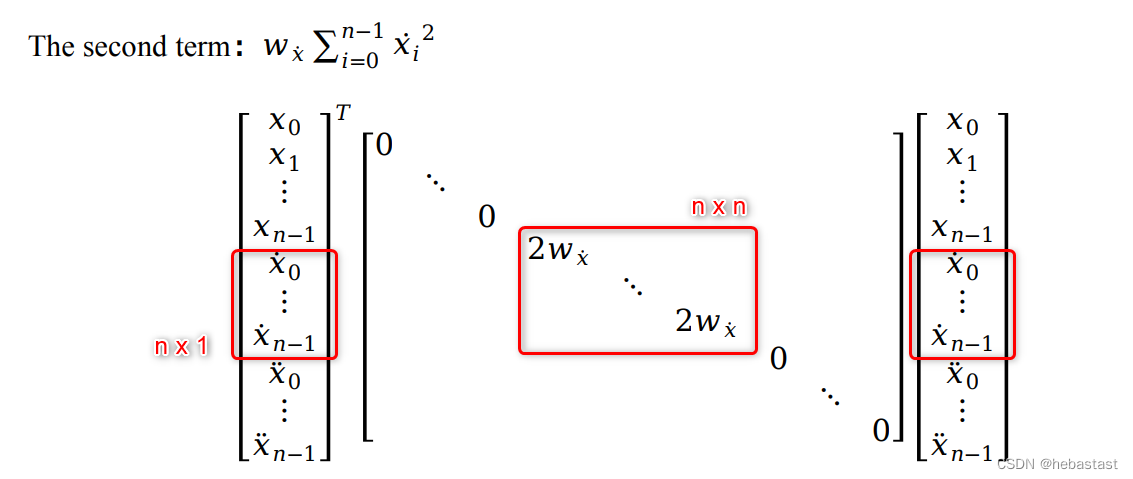
1.2 The second term:
1.3 The thrid term:
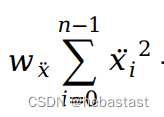
1.4 The forth term:
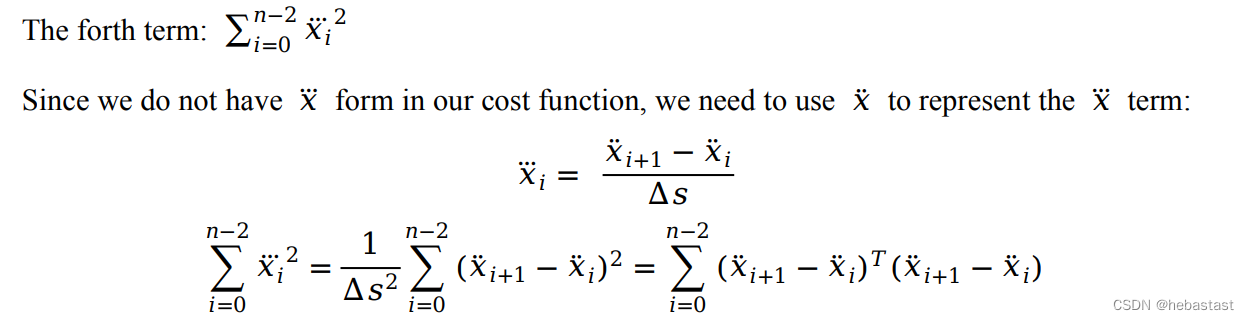

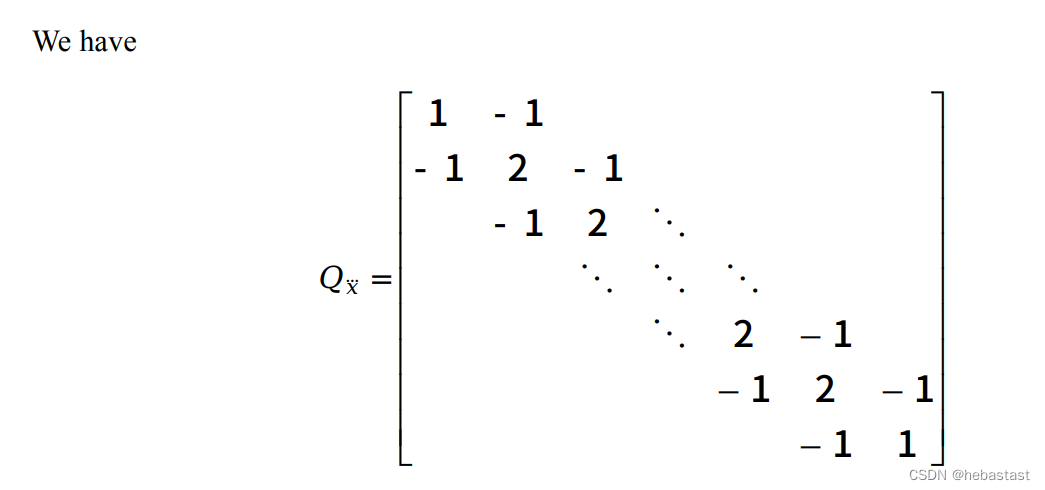
对 Qx''' 矩阵公式的验证
假设有四个点,x1, x2... x3,则:
 使用上面的 matrix form:
使用上面的 matrix form:

说明上述的 Qx''' 的公式是正确的。
整体 Q 矩阵(就是 P 矩阵,二次项的权重矩阵)
所以,cost function 的 Q 矩阵为:

整体 P 矩阵的形式如下:


注意:代码中 Apollo 中的 Q 矩阵(代码中是 P 矩阵)形式与上述推导有一定的差异:

Apollo 6.0 代码中的 P 矩阵形式如下:
参见这篇文章:
https://zhuanlan.zhihu.com/p/480298921
目标函数的形式如下:
 下面就是代码中的 P 矩阵的实际形式:
下面就是代码中的 P 矩阵的实际形式:
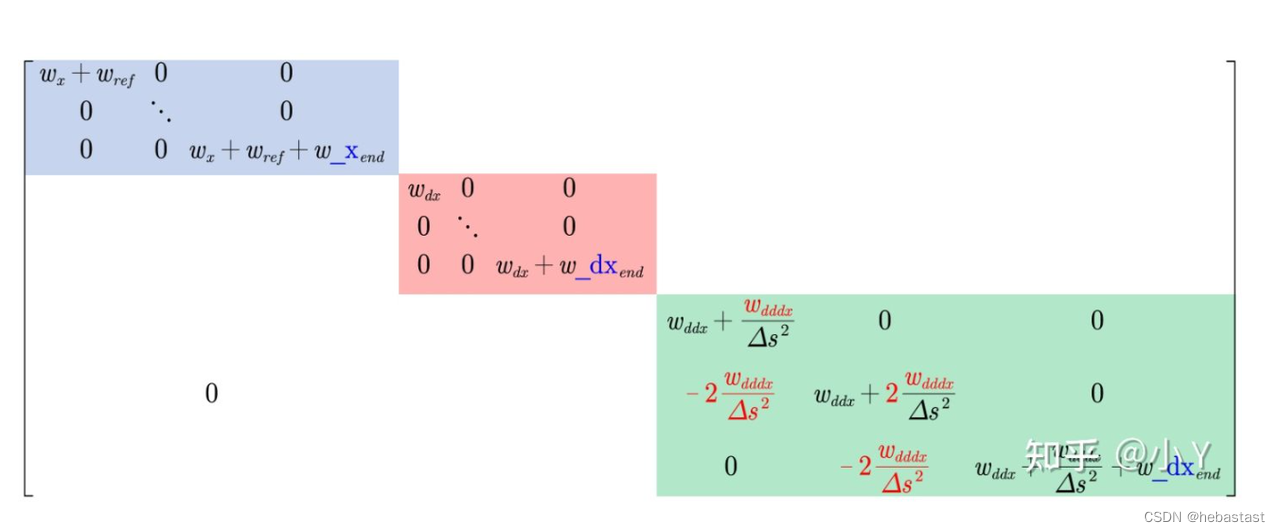
构建 P 矩阵的函数:
void PiecewiseJerkPathProblem::CalculateKernel(std::vector<c_float>* P_data,
std::vector<c_int>* P_indices,
std::vector<c_int>* P_indptr)
P 矩阵的零阶导数(蓝色)部分对应的代码块:

// x(i)^2 * (w_x + w_x_ref[i]), w_x_ref might be a uniform value for all x(i)
// or piecewise values for different x(i)
// P 矩阵的零阶导数部分
for (int i = 0; i < n - 1; ++i) {
columns[i].emplace_back(i, (weight_x_ + weight_x_ref_vec_[i]) /
(scale_factor_[0] * scale_factor_[0])); // scale_factor - 缩放系数
++value_index;
}
// x(n-1)^2 * (w_x + w_x_ref[n-1] + w_end_x) - 最后一个节点增加了一个末状态的权重 w_end_x
columns[n - 1].emplace_back(
n - 1, (weight_x_ + weight_x_ref_vec_[n - 1] + weight_end_state_[0]) /
(scale_factor_[0] * scale_factor_[0]));
++value_index;
P 矩阵的一阶导数(粉色)部分对应的代码块:

// x(i)'^2 * w_dx - P 矩阵的一阶导数部分
for (int i = 0; i < n - 1; ++i) {
columns[n + i].emplace_back(
n + i, weight_dx_ / (scale_factor_[1] * scale_factor_[1]));
++value_index;
}
// x(n-1)'^2 * (w_dx + w_end_dx)
columns[2 * n - 1].emplace_back(2 * n - 1,
(weight_dx_ + weight_end_state_[1]) /
(scale_factor_[1] * scale_factor_[1]));
++value_index;
P 矩阵的二阶导数(绿色)部分对应的代码块:
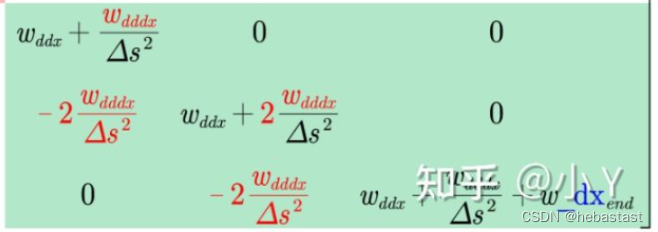
auto delta_s_square = delta_s_ * delta_s_;
// P 矩阵的二阶导数部分的第一个对角线元素
// x(i)''^2 * (w_ddx + 2 * w_dddx / delta_s^2)
columns[2 * n].emplace_back(2 * n,
(weight_ddx_ + weight_dddx_ / delta_s_square) /
(scale_factor_[2] * scale_factor_[2]));
++value_index;
// P 矩阵的二阶导数部分的对角线元素(除了对角线上的第一个元素和最后一个元素)
for (int i = 1; i < n - 1; ++i) {
columns[2 * n + i].emplace_back(
2 * n + i, (weight_ddx_ + 2.0 * weight_dddx_ / delta_s_square) /
(scale_factor_[2] * scale_factor_[2]));
++value_index;
}
// P 矩阵的二阶导数部分的最后一个对角线元素
columns[3 * n - 1].emplace_back(
3 * n - 1,
(weight_ddx_ + weight_dddx_ / delta_s_square + weight_end_state_[2]) /
(scale_factor_[2] * scale_factor_[2]));
++value_index;
// P 矩阵的二阶导数部分的次对角线上的元素
// -2 * w_dddx / delta_s^2 * x(i)'' * x(i + 1)''
for (int i = 0; i < n - 1; ++i) {
columns[2 * n + i].emplace_back(2 * n + i + 1,
(-2.0 * weight_dddx_ / delta_s_square) /
(scale_factor_[2] * scale_factor_[2]));
++value_index;
目标函数中的线性项部分,即 q 矩阵的构建
这部分代码在 PiecewiseJerkPathProblem::CalculateOffset 这个函数
void PiecewiseJerkPathProblem::CalculateOffset(std::vector<c_float>* q)
q 矩阵形式如下:

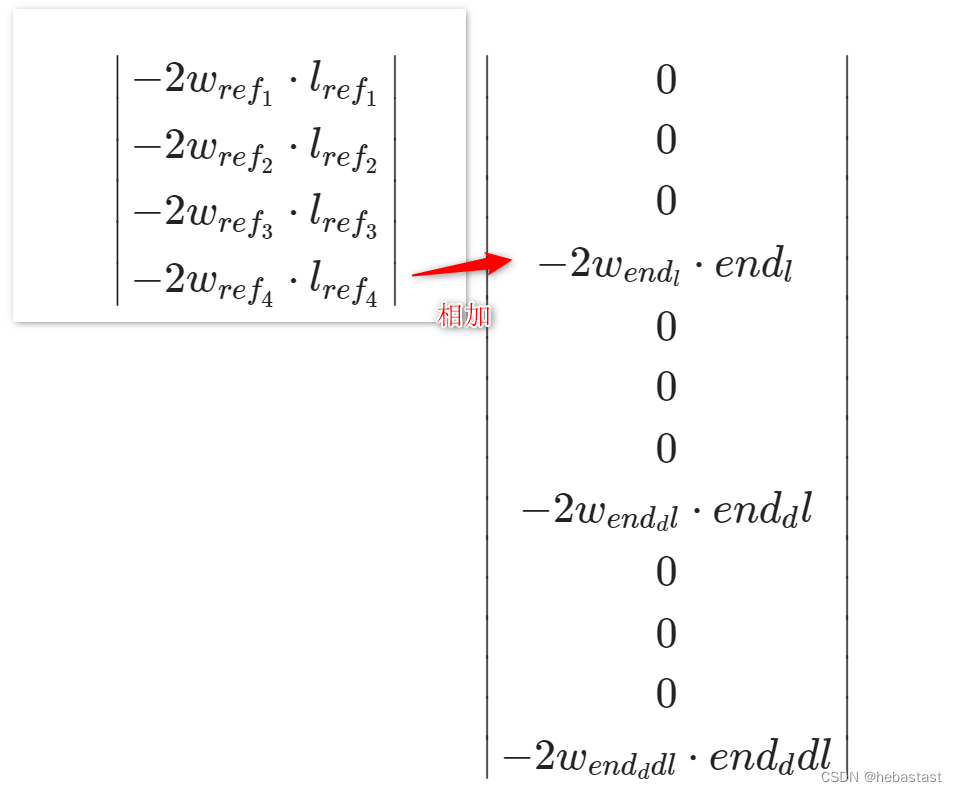
计算 q 矩阵的代码块如下:
if (has_x_ref_) {
for (int i = 0; i < n; ++i) {
q->at(i) += -2.0 * weight_x_ref_vec_.at(i) * x_ref_[i] / scale_factor_[0];
}
}
//
if (has_end_state_ref_) {
q->at(n - 1) +=
-2.0 * weight_end_state_[0] * end_state_ref_[0] / scale_factor_[0];
q->at(2 * n - 1) +=
-2.0 * weight_end_state_[1] * end_state_ref_[1] / scale_factor_[1];
q->at(3 * n - 1) +=
-2.0 * weight_end_state_[2] * end_state_ref_[2] / scale_factor_[2];
}
2. Constraints
2.1 不等式约束

2.2 连续性约束
用每个轨迹点处在 l 方向的 jerk 相等作为连续性约束。

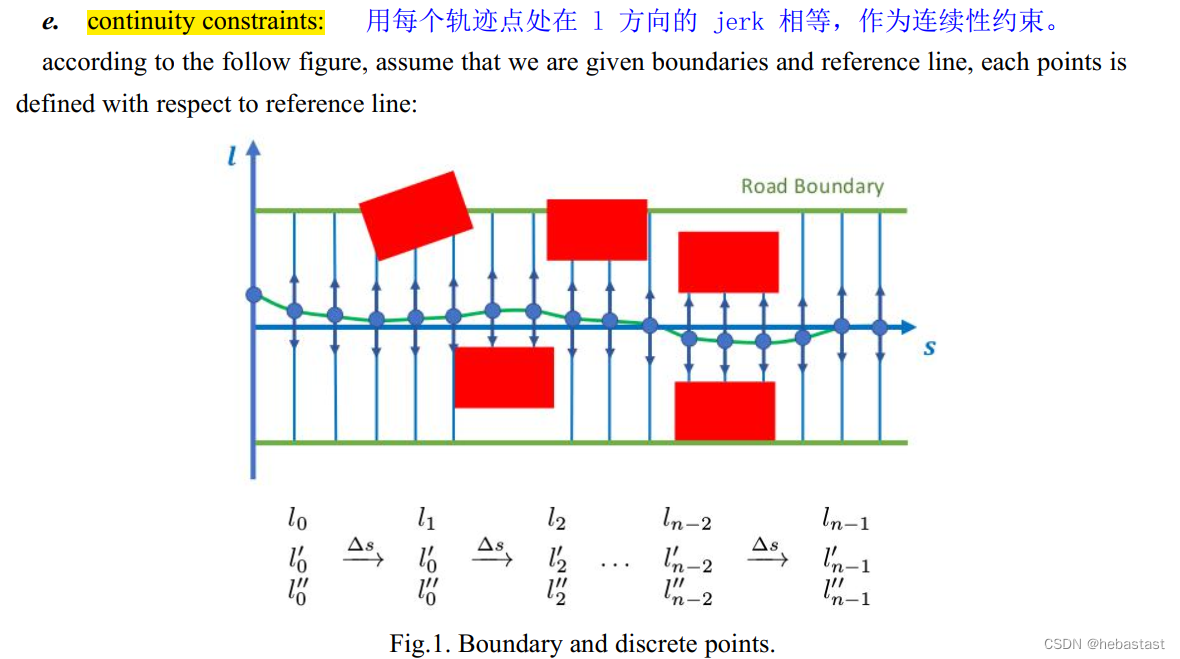
上面的推导和下面的推导是一致的:

将 piecewise jerk 的条件带入:
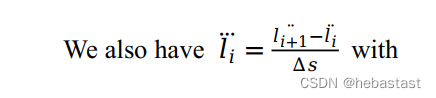
得:
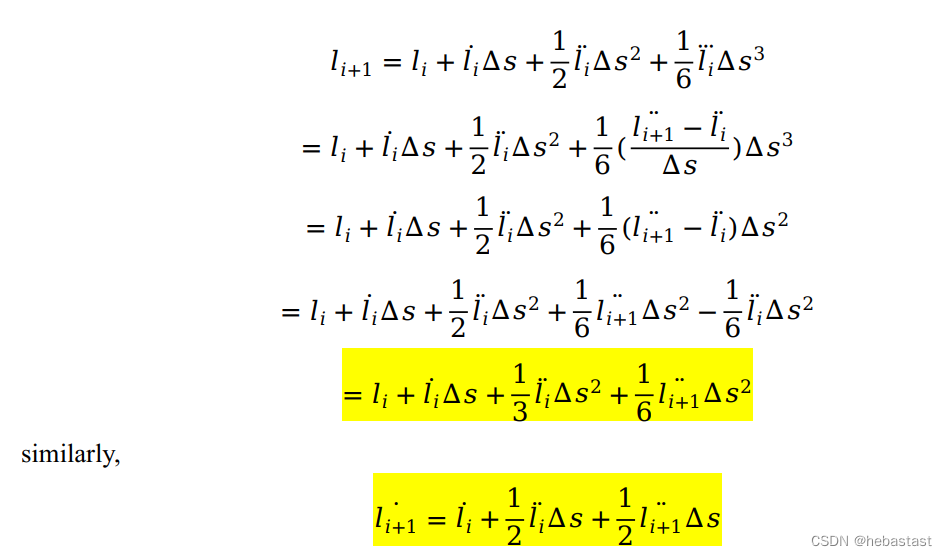
Now we generate constraints in matrix form.
![]()
For constrains a - lateral offset - 0 阶导数
 For constrains b - lateral velocity - 一阶导数
For constrains b - lateral velocity - 一阶导数

For constrains c - lateral acceleration - 二阶导

For constraints d - lateral jerk - 三阶导数
这里有一些问题,对于 jerk 的不等式约束,应该是下面的形式:

For constraints e - 连续性约束

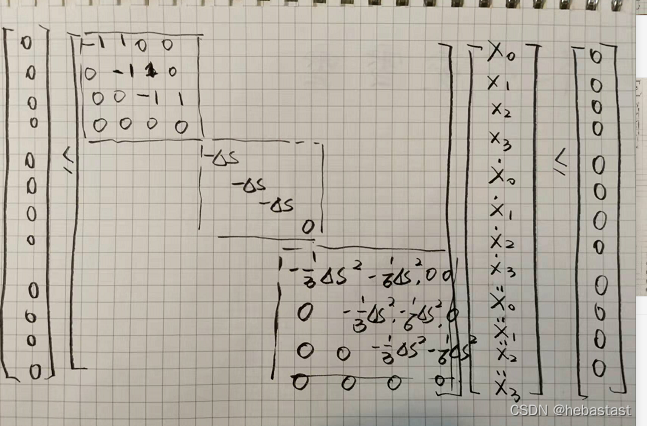
下图是有四个点的时候仿射矩阵的具体形式:

For Constraints f:

约束可以写成:
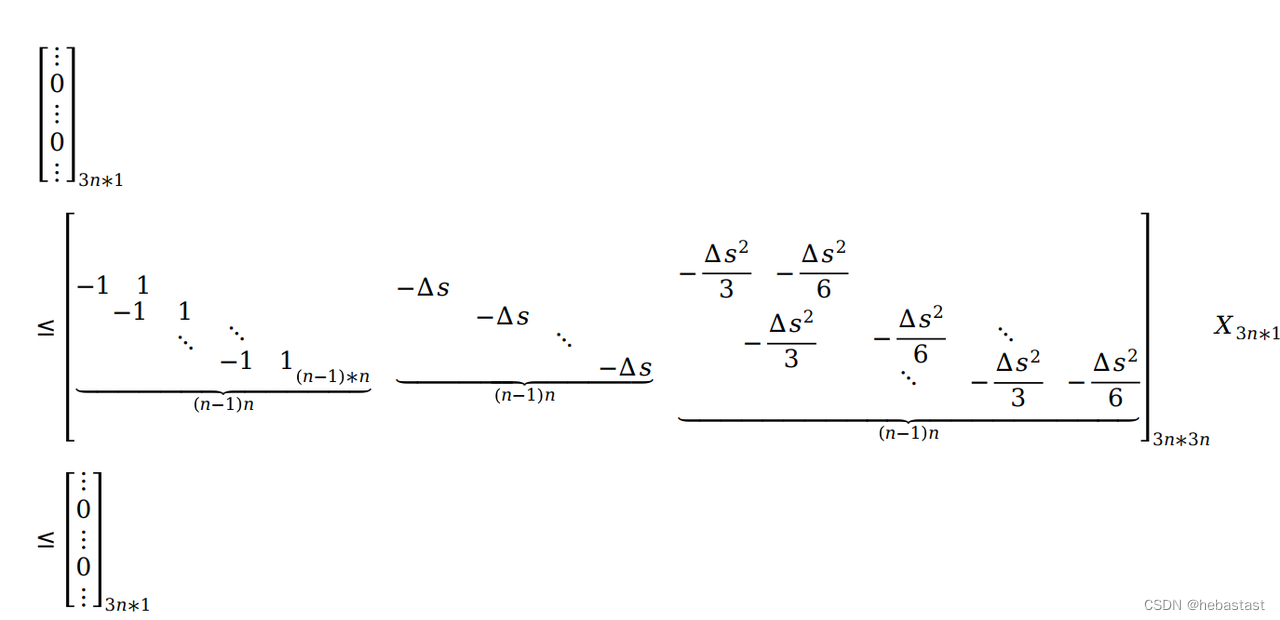
具体形式:
Equality constraints

不等式约束的上下边界条件为:



上下边界条件是如何计算的?
关于边界约束的详细介绍参见这篇文章:https://zhuanlan.zhihu.com/p/481835121
二阶导边界极值的计算:

对应代码如下:
const double lat_acc_bound =
std::tan(veh_param.max_steer_angle() / veh_param.steer_ratio()) /
veh_param.wheel_base();
std::vector<std::pair<double, double>> ddl_bounds;
for (size_t i = 0; i < path_boundary_size; ++i) {
double s = static_cast<double>(i) * path_boundary.delta_s() +
path_boundary.start_s();
double kappa = reference_line.GetNearestReferencePoint(s).kappa();
ddl_bounds.emplace_back(-lat_acc_bound - kappa, lat_acc_bound - kappa);
}
三阶导边界极值的计算


最后,A 矩阵为:

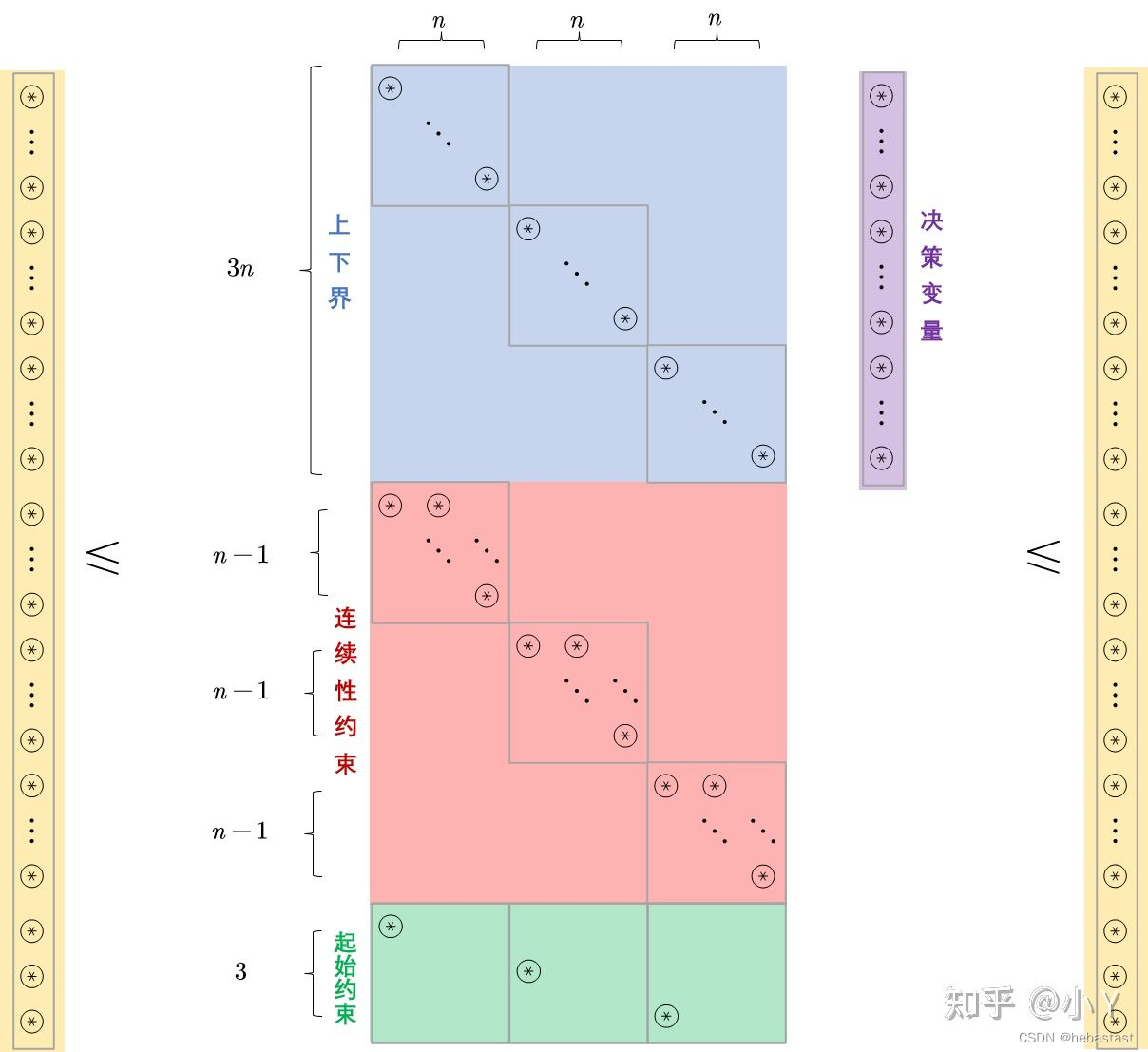
仿射矩阵 A
至此,P 矩阵,q 矩阵,A 矩阵,b 矩阵均可以表示出来,放入 OSQP 求解器中,可以进行迭代求解了。

The Principle of Apollo Path Planning using Quadratic Programming
这里是 Piecewise Jerk Path Optimizer 的代码讲解。
这篇关于自动驾驶规划中使用 OSQP 进行二次规划 代码原理详细解读的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






