本文主要是介绍【数据结构与算法】图的存储(邻接矩阵,邻接表)详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
图的邻接矩阵数据结构
typedef enum { NDG, DG, NDN, DN } GraphKind;using VRType = int;
using InfoType = int;typedef struct ArcCell {VRType adj;InfoType *info;
} Arc[N][N];struct MGraph {ElemType vexs[N];Arc arc;int vexnum, arcnum;GraphKind kind;
};
ArcCell 结构体包含两个成员:
adj是一个VRType类型的变量,表示顶点之间的关系,例如,如果两个顶点之间存在边,那么adj表示这条边的权重。info是一个指向InfoType类型的指针,用于存储与边相关的额外信息。
MGraph 结构体包含四个成员:
vexs是一个ElemType类型的数组,用于存储图的顶点。arc是一个Arc类型的二维数组,用于存储图的边。vexnum是一个整数,表示图的顶点数量。arcnum是一个整数,表示图的边数量。kind是一个GraphKind类型的枚举,表示图的类型。
图的数组表示法、邻接表存贮结构各自的优缺点,适应的运算。
-
图的数组表示法(邻接矩阵):
- 优点:容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
- 缺点:n个顶点需要n*n个单元存储边(弧);空间效率为 O ( n 2 ) O(n^2) O(n2)。 对稀疏图而言尤其浪费空间。
- 适应的运算:边的数量较多,需要频繁检查节点间是否存在边的场景。

-
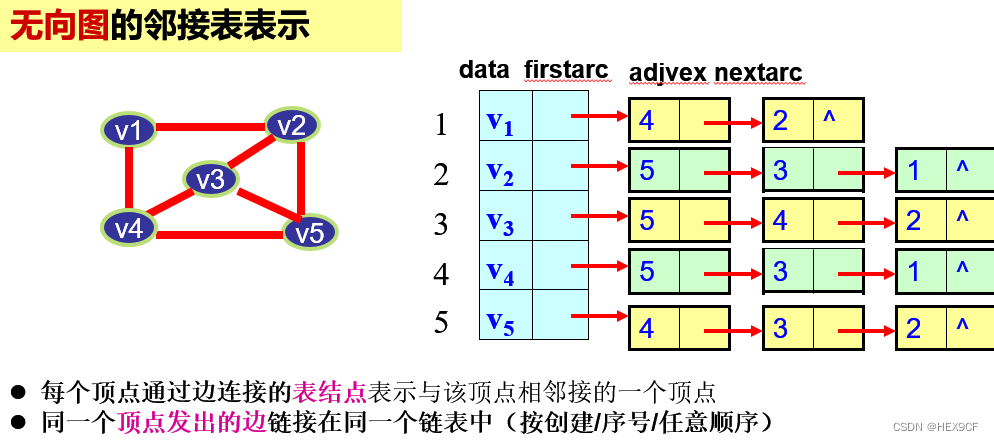
图的邻接表存储结构:
- 优点:n个顶点、e条边的无向图,只需要n个头结点和2e个表结点。对稀疏图而言,比数组表示法节省存储空间。
- 缺点:每条边需要对应两个表结点。
- 适应的运算:边的数量较少,需要频繁添加或删除边的场景。
这篇关于【数据结构与算法】图的存储(邻接矩阵,邻接表)详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





