分治精炼宝库----归并排序应用( ´◔︎ ‸◔︎`)

本文主要是介绍分治精炼宝库----归并排序应用( ´◔︎ ‸◔︎`)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一.基本概念:

二.归并排序：

三.交易逆序对总数：

四.计算右侧小于当前元素的个数：

五.翻转对：

六.合并k个有序链表：

一.基本概念:

🐻在计算机科学中，分治法是一种很重要的算法。字面上的解释就是“分而治之”，就是把一个复杂的问题分成两个或则更多个相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法（快速排序，归并排序），傅立叶变换(快速傅立叶变换)……

　任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。例如，对于n个元素的排序问题，当n=1时，不需任何计算。n=2时，只要作一次比较即可排好序。n=3时只要作3次比较即可，…。而当n较大时，问题就不那么容易处理了。要想直接解决一个规模较大的问题，有时是相当困难的。🧐分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

当我们对分治算法有了以上的一定了解后，来联系几道题目加深理解~~

二.归并排序：

归并排序的流程充分的体现了「分⽽治之」的思想，⼤体过程分为两步：

分：将数组⼀分为⼆为两部分，⼀直分解到数组的⻓度为1 ，使整个数组的排序过程被分为「左半部分排序」+「右半部分排序」；
治：将两个较短的「有序数组合并成⼀个⻓的有序数组」，⼀直合并到最初的⻓度。

大致图解过程（图中例子为主）：

咱们以leetcode排序数组题目为例：912. 排序数组 - 力扣（LeetCode）

代码详解：

class Solution {int[] tmp;public int[] sortArray(int[] nums) {int n = nums.length;tmp = new int[n];mergeSort(nums,0,n - 1);return nums;}public void mergeSort(int[] nums,int left,int right){if(left >= right) return ;//取中点划分区域//[left,mid] [mid + 1,right];int mid = left + (right - left) / 2;//排序划分的左数组和右数组mergeSort(nums,left,mid);mergeSort(nums,mid + 1,right);//合并两个有序数组int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur1++];}else{tmp[i++] = nums[cur2++];}}//处理没有完全合并的数组while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];//还原数组for(int j = left;j <= right;j++){nums[j] = tmp[j - left];}}}

我们提取一下主要框架，大致就是：

看这个框架，也就明白那句经典的总结：归并排序就是先把左半边数组排好序，再把右半边数组排好序，然后把两半数组合并。

运行结果：

三.交易逆序对总数：

题目链接：LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

题目描述：

在股票交易中，如果前一天的股价高于后一天的股价，则可以认为存在一个「交易逆序对」。请设计一个程序，输入一段时间内的股票交易记录 record，返回其中存在的「交易逆序对」总数。

算法思路：

如果我们将数组从中间划分成两个部分，那么我们可以将逆序对产⽣的⽅式划分成三组：

逆序对中两个元素：全部从左数组中选择
逆序对中两个元素：全部从右数组中选择
逆序对中两个元素：⼀个选左数组另⼀个选右数组

根据排列组合的分类相加原理,这三种情况下的逆序对总和，就是总的逆序对总和。不难发现，这其实和归并排序的主过程一致，所以我们可以利用归并排序的特性，先计算左半部分数组的逆序对，再计算右半部分数组的逆序对数，最后计算一左一右的逆序对个数。三者相加，就是总的逆序对个数。

合并操作时，计算一左一右的逆序对个数：

此时mergeSort(nums,0,nums.length - 1) 就有了新的定义，计算并返回数组区间[0 , nums.length - 1] 的逆序对个数

代码详解：

class Solution {int[] tmp;public int reversePairs(int[] record) {int n = record.length;tmp = new int[n];return mergeSort(record,0,n - 1);}public int mergeSort(int[] nums,int left,int right){if(left >= right) return 0;//取中间点划分区间int mid = left + (right - left)/ 2;//[left,mid][mid + 1,right];int res = 0;//记录结果res += mergeSort(nums,left,mid);res += mergeSort(nums,mid + 1,right);//合并两个有序数组，计算逆序对个数int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur1++];}else{res += mid - cur1 + 1;tmp[i++] = nums[cur2++];}}//处理没有完全合并的数组while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];//还原数组for(int j = left;j <= right;j++){nums[j] = tmp[j - left];}return res;}
}

运行结果：

四.计算右侧小于当前元素的个数：

题目链接：315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

题目描述：给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

算法思路：

这⼀道题的解法与求数组中的逆序对的解法是类似的，但是这⼀道题要求的不是求总的个数，⽽是要返回⼀个数组，记录每⼀个元素的右边有多少个元素⽐⾃⼰⼩。但是在我们归并排序的过程中，元素的下标是会跟着变化的，因此我们需要⼀个辅助数组，来将数组元素和对应的下标绑定在⼀起归并，也就是再归并元素的时候，顺势将下标也转移到对应的位置上。由于我们要快速统计出某⼀个元素后⾯有多少个⽐它⼩的,所以我们采用降序策略：

代码详解：

class Solution {int[] tmp1;int[] tmp2;int[] index;//记录数组下标位置int[] res;//记录结果List<Integer> ret = new ArrayList<>();//记录返回结果public List<Integer> countSmaller(int[] nums) {int n = nums.length;tmp1 = new int[n];tmp2 = new int[n];res = new int[n];index = new int[n];//初始化坐标位置for(int i = 0;i < n;i++) index[i] = i;mergeSort(nums,0,n - 1);for(int i = 0;i < n;i++) ret.add(res[i]);return ret;}public void mergeSort(int[] nums,int left,int right){if(left >= right) return ;//取中间划分区域int mid = left + (right - left) / 2;mergeSort(nums,left,mid);mergeSort(nums,mid + 1,right);//合并数组，计算逆序对个数int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp1[i] = nums[cur2];tmp2[i++] = index[cur2++];}else{res[index[cur1]] += right - cur2 + 1;tmp1[i] = nums[cur1];tmp2[i++] = index[cur1++];}}//处理没有完全合并的数组while(cur1 <= mid){tmp1[i] = nums[cur1];tmp2[i++] = index[cur1++];}while(cur2 <= right){tmp1[i] = nums[cur2];tmp2[i++] = index[cur2++];}//还原数组for(int j = left;j <= right;j++){nums[j] = tmp1[j - left];index[j] = tmp2[j - left];}}
}

运行结果：

五.翻转对：

题目链接：493. 翻转对 - 力扣（LeetCode）

题目描述：

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

算法思路：

大思路与求逆序对的思路一样，就是利用归并排序的思想，将求整个数组的翻转对的数量，转化成三部分：左半区间翻转对的数量，右半区间翻转对的数量，一左一右选择时翻转对的数量。重点实在合并过程中，如何计算出翻转对的数量。与上个问题不同的是，上一道题我们可以一边合并一边计算结果，但是这道题左边元素大于右边元素的两倍的条件不符合归并排序时的特性，如果我们直接合并，是无法计算出翻转对的个数的，因此我们要再归并排序的合并之前，排序之后完成对翻转对的统计。

代码详解：

class Solution {int[] tmp;public int reversePairs(int[] nums) {int n = nums.length;tmp = new int[n];return mergeSort(nums,0,n - 1);}public int mergeSort(int[] nums,int left,int right){if(left >= right) return 0;//取中间点划分区间int mid = left + (right - left) / 2;int res = 0;//记录结果//[left,mid] [mid + 1,right]res += mergeSort(nums,left,mid);res += mergeSort(nums,mid + 1,right);int cur1 = left,cur2 = mid + 1,i = 0;//计算翻转对while(cur1 <= mid){//注意处理越界情况while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0) cur2++;if(cur2 > right){break;}res += right - cur2 + 1;cur1++;}//合并有序数组cur1 = left;cur2 = mid + 1;//重置一下while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur2++];}else {tmp[i++] = nums[cur1++];}}//处理还没有完全合并的数组while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];//还原数组for(int j = left;j <= right;j++){nums[j] = tmp[j - left];}//返回结果return res;} 
}

运行结果：

六.合并k个有序链表：

题目链接：23. 合并 K 个升序链表 - 力扣（LeetCode）

题目描述：

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

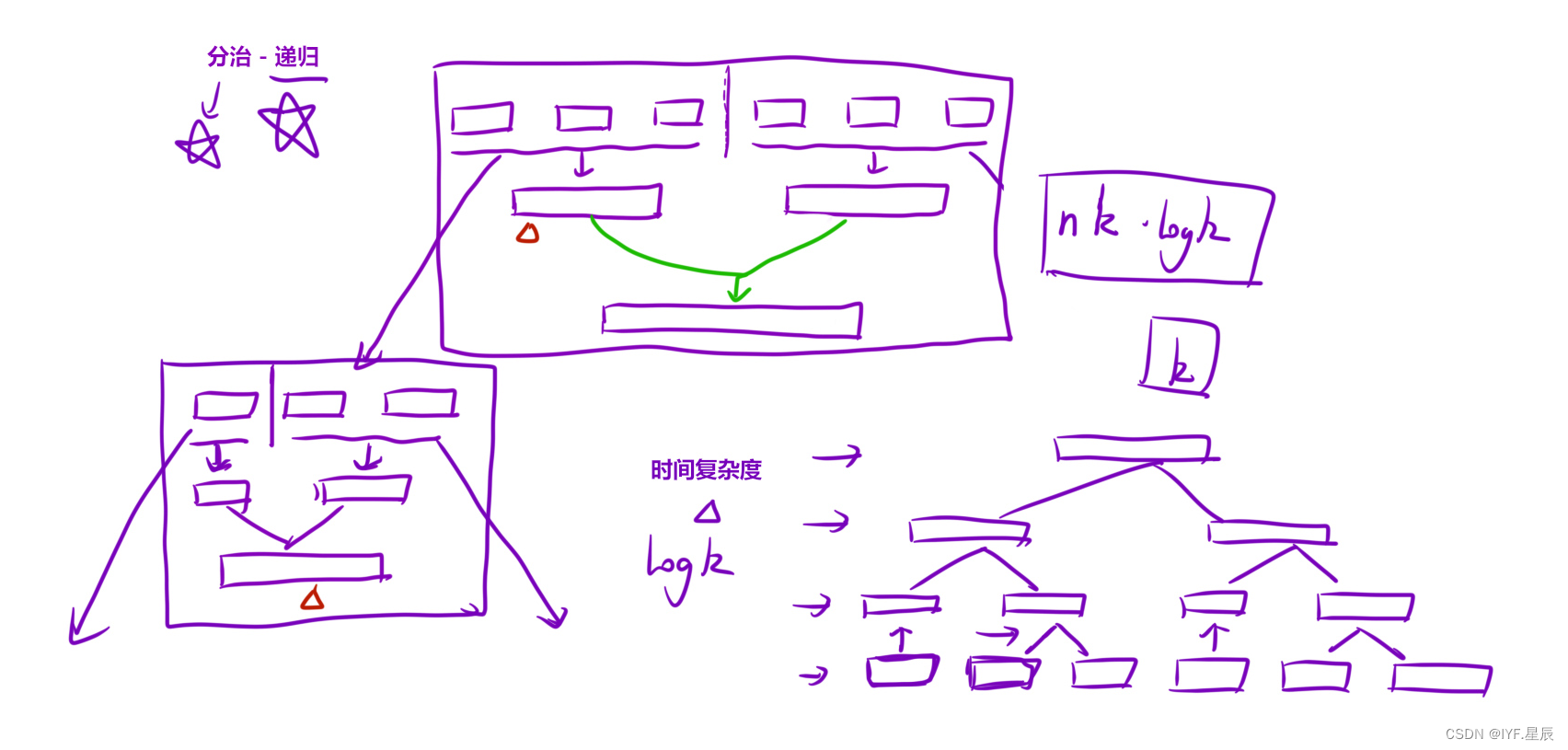
解法一：分治

思路：与归并排序数组一样的原理，只不过这里的合并过程是合并两个有序链表，而排序数组是合并两个有序数组。

代码详解：

class Solution {ListNode[] tmp;public ListNode mergeKLists(ListNode[] lists) {if(lists.length == 0) return null;return mergeSort(lists,0,lists.length - 1);}public ListNode mergeSort(ListNode[] lists,int left,int right){if(left >= right) return lists[left];//取中间节点划分两部分int mid = (left + right) / 2;//[left,mid] [mid + 1,right]ListNode l1 =  mergeSort(lists,left,mid);ListNode l2 = mergeSort(lists,mid + 1,right);//合并两个有序链表return merge(l1,l2);}public ListNode merge(ListNode l1,ListNode l2){if(l1 == null) return l2;if(l2 == null) return l1;ListNode cur1 = l1,cur2 = l2;ListNode res = new ListNode(-1);//虚拟节点ListNode pre = res;while(cur1 != null && cur2 != null){if(cur1.val <= cur2.val){pre.next = cur1;pre = cur1;cur1 = cur1.next;}else{pre.next = cur2;pre = cur2;cur2 = cur2.next;}}if(cur1 != null) pre.next = cur1;if(cur2 != null) pre.next = cur2;return res.next;}}

解法二：利用数据结构---堆

算法思路：

合并K 个升序链表时，我们依旧可以选择K 个链表中，头结点值最⼩的那⼀个。那么如何快速的得到头结点最⼩的是哪⼀个呢？⽤堆这个数据结构就好啦~ 我们可以把所有的头结点放进⼀个⼩根堆中，这样就能快速的找到每次K 个链表中，最⼩的元素是哪个。然后我们取出最小的节点合并，再将其后面一个位置的索引丢入到小根堆中。

代码详解：

class Solution {public ListNode mergeKLists(ListNode[] lists) {//定义一个优先级队列，排序规则是从小到大PriorityQueue<ListNode> heap = new PriorityQueue<>((v1,v2)-> v1.val - v2.val);//将所有头节点放入到优先级队列中for(ListNode head : lists){if(head != null){heap.offer(head);}}//合并链表ListNode res = new ListNode(-1);//虚拟节点ListNode pre = res;while(!heap.isEmpty()){ListNode t = heap.poll();pre.next = t;pre = t;if(t.next != null) heap.offer(t.next);}return res.next;}
}