本文主要是介绍动态规划02(Leetcode62、63、343、96),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:
https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html
62. 不同路径
题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
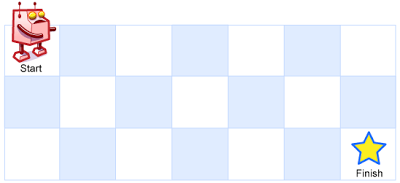
输入:m = 3, n = 7 输出:28
思路分析:
本题思路简单,按照动规五步即可实现。
状态压缩:二维 ——> 一维
代码实现:
//动规
//1.dp[i][j]:到达点(i,j)的路径数
class Solution {public int uniquePaths(int m, int n) {int[][] dp=new int [m][n];//3.初始化for(int i=0;i<m;i++){dp[i][0]=1;}for(int j=0;j<n;j++){dp[0][j]=1;}//4.遍历顺序for(int i=1;i<m;i++){//行for(int j=1;j<n;j++){//列//2.递推公式dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1]; }
}//状态压缩
class Solution {public int uniquePaths(int m, int n) {int[] dp=new int[n];Arrays.fill(dp,1);//第一行只有一条路径到for(int i=1;i<m;i++){for(int j=1;j<n;j++){//第一列也只有一条路dp[j]+=dp[j-1];//dp[j]=dp[j](上方来)-dp[j-1](左边来)}}return dp[n-1];}
}63. 不同路径 II
题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
思路分析:
整体思路与上题一样。
区别:本题在初始化和遍历过程中增加障碍物的条件判断即可。
代码实现:
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m=obstacleGrid.length;int n=obstacleGrid[0].length;int[][] dp=new int[m][n];if(obstacleGrid[m-1][n-1]==1 || obstacleGrid[0][0]==1) return 0;for(int i=0;i<m && obstacleGrid[i][0]==0;i++){dp[i][0]=1;}for(int j=0;j<n&&obstacleGrid[0][j]==0;j++){dp[0][j]=1;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==1){dp[i][j]=0;continue;}dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];}
}//压缩
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m=obstacleGrid.length;int n=obstacleGrid[0].length;int[] dp=new int[n];for(int j=0;j<n&&obstacleGrid[0][j]==0;j++){//第一行dp[j]=1;}for(int i=1;i<m;i++){for(int j=0;j<n;j++){if(obstacleGrid[i][j]==1){dp[j]=0;}else if(j!=0){dp[j]+=dp[j-1];}}}return dp[n-1];}
}343. 整数拆分
题目描述:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
思路分析:
状态转移方程=拆成2个数 + 拆成3个数及以上
初始化 dp[2]=1
优化:j 遍历到 i/2 即可,再往后就重复遍历了
代码实现:
//dp[i]:数i拆分后的数乘积最大值为dp[i]
class Solution {public int integerBreak(int n) {if(n==2) return 1;int[] dp=new int[n+1];dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<=i/2;j++){dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));//j*(i-j)拆成两数//j*dp[i-j]拆成两数以上}}return dp[n];}
}96. 不同的二叉搜索树
题目描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
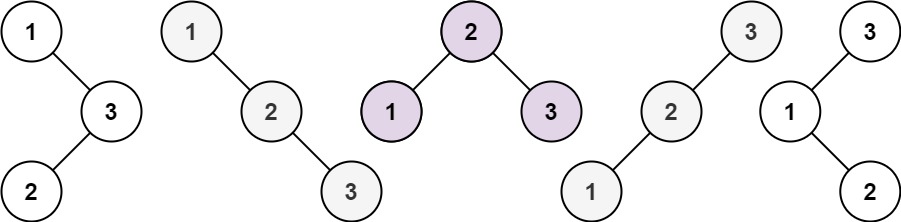
输入:n = 3 输出:5
思路分析:
初始化:空节点对应一种情况,1个节点对应一种情况
递推公式:头结点从1到n遍历,将每个情况相加
代码实现:
class Solution {public int numTrees(int n) {if(n==1) return 1;int[] dp=new int[n+1];dp[0]=1;dp[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){//以j为头结点dp[i]+=dp[j-1]*dp[i-j];//左*右}}return dp[n];}
}这篇关于动态规划02(Leetcode62、63、343、96)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




